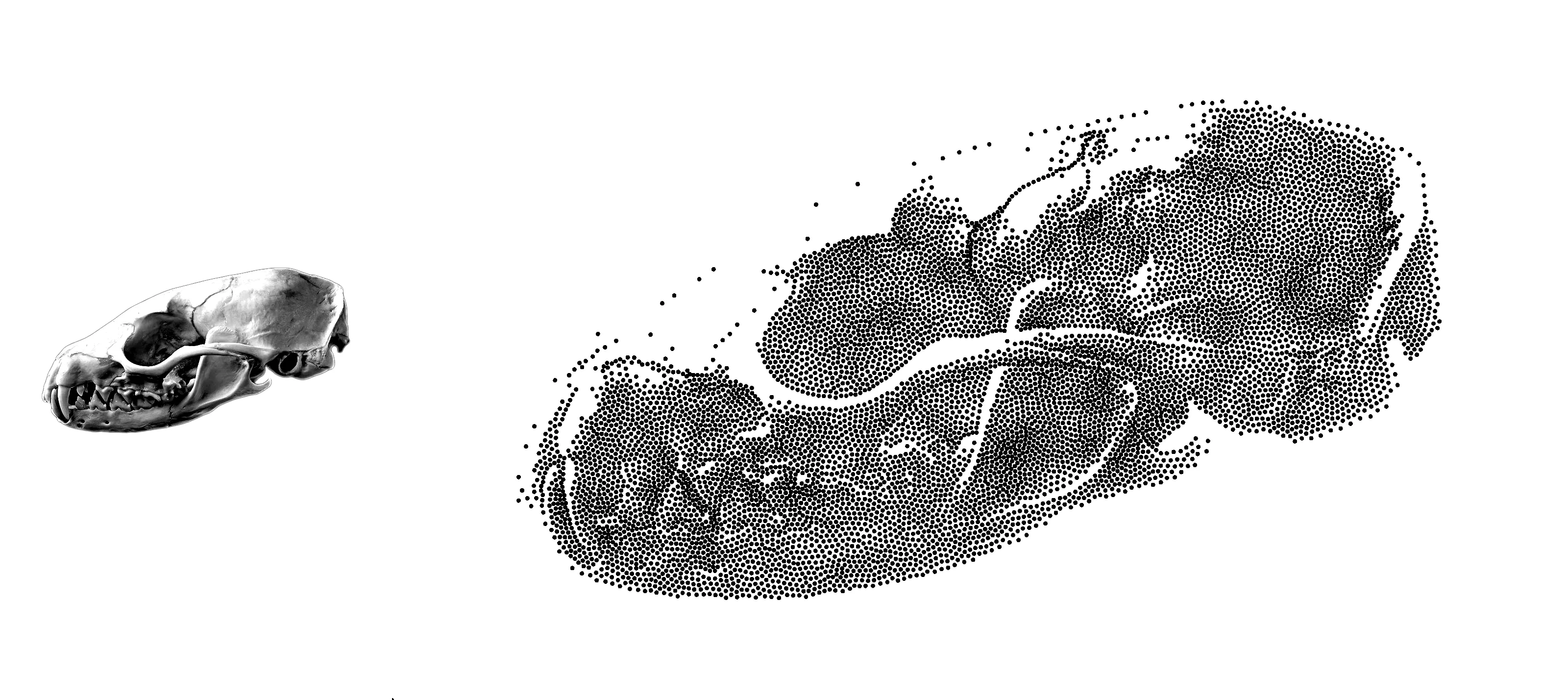
Left: Pine Marten skull image taken from Wikimedia Commons. Background was removed, converted to greyscale and contrast increased. Right: is the stippled image using approximately 10000 points.
Stippling is the process of representing an image using a collection of small dots, similar to dithering but without the restriction that the points be placed on a grid. While stippling was originally borne out of the necessity for easier replication of textbook diagrams, the technique has artistic merit worth exploring for its own sake. In the paper Weighted Voronoi Stippling Adrian Secord presents a technique for automatically stippling an image based upon a modification to Lloyd’s iterative algorithm for Centroidal Voronoi diagrams.
Voronoi diagrams are a partition of a metric space into regions for which a given site point (from a provided set of site points) is the closest to any contained point by our chosen metric. In the case of centroidal Voronoi diagrams these site points are also the center of mass of the region.
In the placement of points in stippling we desire a distribution in which the distance between points corresponds to the value of the image being represented near that region, and without obvious patterns to distract the eye. Centroidal voronoi diagrams are good at producing what is known as blue noise, set of points which are spaced from each other by no more than a set distance, and had been used in previous stippling methods for smoothing point distributions. Secord’s contribution is a simple one, but ingenious: instead of a constant density in the calculation of the centroids, we can use the image values to determine the density such that darker areas will end up with more points, and lighter areas will end up with less. Instead of smoothing as a separate step, the points can be generated and smoothed in a single process.
While the method is elegant and produces good results, there are several significant drawbacks. Lloyd’s algorithm is iterative and converges slowly in practice, and calculation of the centroids is an inherently serial accumulation which makes it hard to parallelize. The method presented for computing the Voronoi regions is fast but also heavily depends on resolution, and an accurate method such as Fortune’s algorithm is potentially much slower. A hybrid approach is suggested by Secord to address the performance, at the cost of visual quality, though ultimately the method remains ill suited for real-time applications.
Finally there is to my knowledge still no theoretical proof for convergence of Lloyd’s algorithm. In addition, the solution which the algorithm converges upon (if it does converge) is not necessarily a global solution.
The implementation which I now present was written using C++ and OpenGL for rendering the Voronoi regions, and OpenMP for the computation of the integral. Boost’s Generic Image Library (GIL) was used for image formats and for conversion and scaling, and Simple Direct Media Layer (SDL) was used to handle OpenGL context creation and windowing.
To begin, the image is scaled up using bilinear sampling with a supplied
scaling factor to ensure that the corresponding Voronoi diagram will
have a large enough resolution for accurate convergence. Then it is
converted to a floating point image and inverted to form our density
map. From this we obtain P by computing the cumulative sum in the X
axis for each row, and from P we do the same to obtain Q. Both
of these are used in the formulation of the integral for centroid
calculations.
An initial distribution is formed by using a uniform distribution across the image and rejecting points which fall on areas of close to zero density. Only the core algorithm was implemented, no hybrid approach has been attempted.
To render a Voronoi diagram, a right cone (base extending out towards the far plane) is instanced for each site point. The site points are sent to the shader as a floating point texture which can then be indexed by instance ID. Each cone is rendered onto a framebuffer with a flat color corresponding to their ID (see figure below). Depth testing must be enabled for this so that the final value present at any given pixel is the closest to the view. Because of the construction of our scene this is also the ID of the closest site point.
The resulting framebuffer is then read back to the CPU for the
computation of the integral. Each row is divided into intervals based on
which regions of the Voronoi diagram they belong. We can now use the
cumulative sum P of the density function for each row, and P’s
cumulative sum Q to evaluate the integrals required for the
centroid.
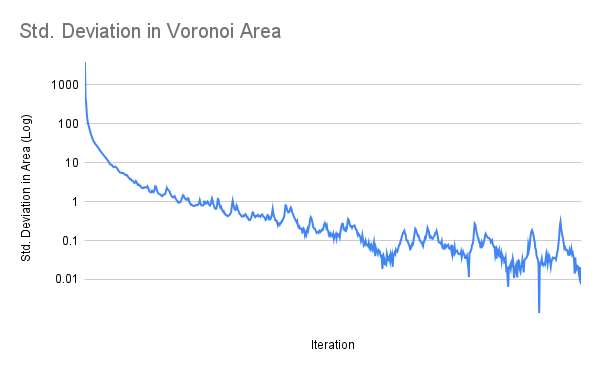
The process is now repeated using the centroids as the new site points and computing another Voronoi diagram with them. The standard deviation of each Voronoi region’s area is calculated and compared against the previous iteration as a stopping condition. An interactive mode is also provided where the user may stop the process when the results are close enough visually.
Once the points have sufficiently converged (or has been stopped by the user) they are rendered as circular disks using another OpenGL shader. Points which lie on nearly white areas of the original image are not rendered, as in the original paper.
The figure above shows the results of an image from the original paper (obtained from here). While the results seem comparable in quality, there are subtle differences worth noting. One in particular can be observed in the Figure 3 from points becoming ’gridlocked’ when surrounded by areas of low density. This lack of global convergence may have been a secondary motivation for the author having a better initial distribution.
The size of the points relative to the image also seems to have a large effect upon the range of perceptual values possible. For the results presented I attempted to choose a point size which would maximize this range simply through trial and error, typically finding a value such that there was overlap in the points and then reducing it to a reasonable level from there. Taking this size into account automatically in the density function would be an area of potential improvement for the method.
The plot above shows the convergence of the standard deviation in Voronoi areas for the shoe image above. A logarithmic scale has been chosen to emphasize the the increasingly chaotic pattern in convergence. This was a particularly extreme example, however all images seemed to similarly fluctuate to some degree.
The other parameter which greatly affects the outcome is the total number of points. Secord suggests that the results are most interesting in what he considers to be a middle range. The actual number also depends upon the size of the image. Besides its artistic merit, slow convergence may also encourage one to keep the number of points low.
A final remark is that subtle gradients do not seem to preserve well when stippled, and a certain amount of perceptual flattening of the image can be observed. This is particularly noticeable in the skull example above. I believe another source of improvement would be to introduce a secondary way of presenting depth cues to the viewer such as through flow of points around contours like we have seen with hatching.