ESKF-Attitude-Estimation

Use Error-State KF algorithm to estimate attitude. The test data can be downloaded here.

修改部分

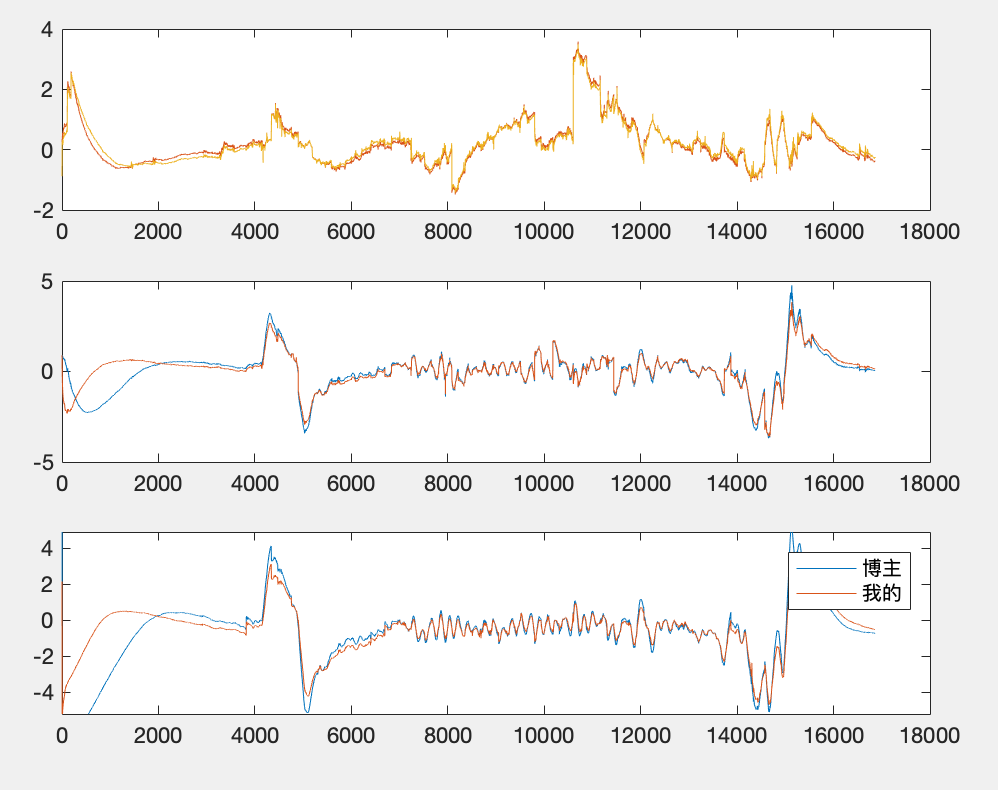
对比我的代码与博主的代码对比

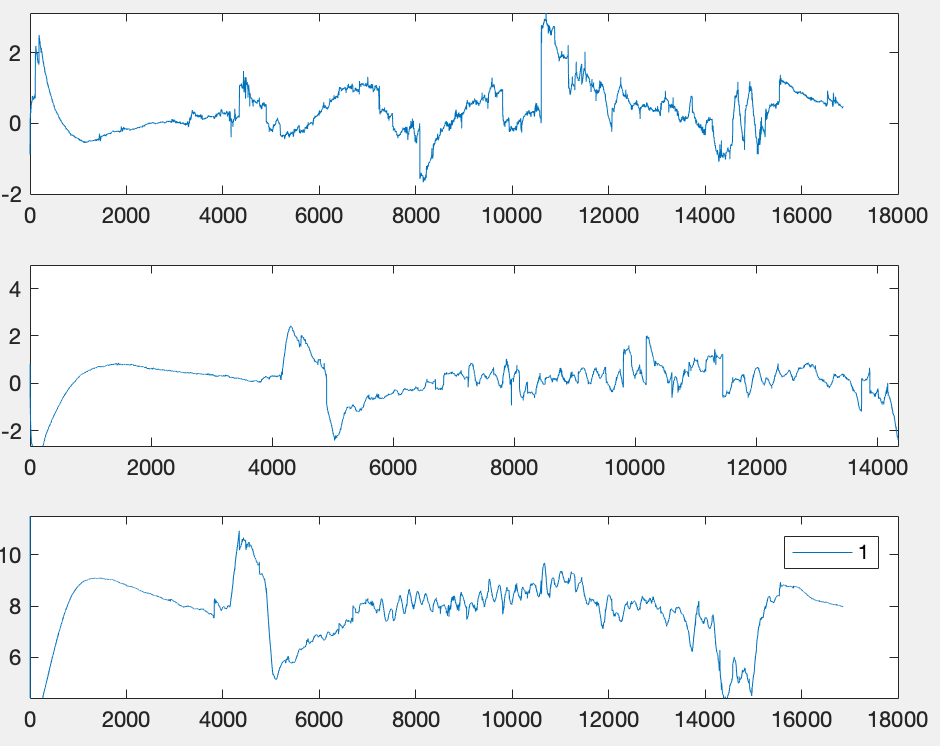
博主的实验，将误差直接除以2，不知为何

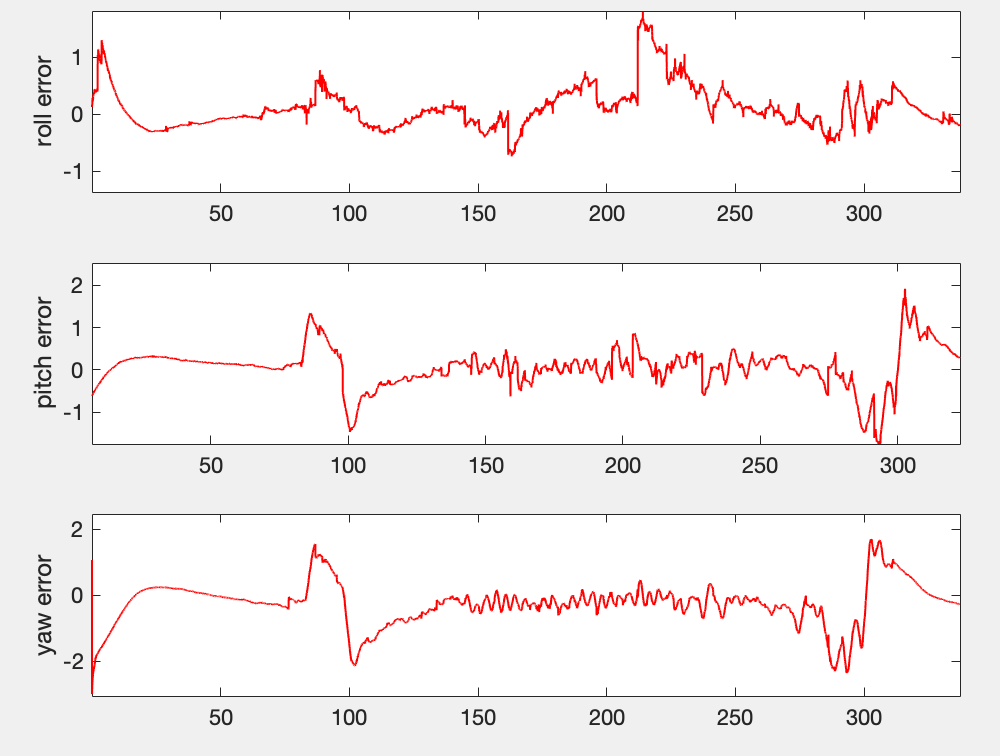
我做的ESKF

可见误差roll与pitch的误差大概是两倍左右。但是yaw的误差相比之下比较大，但是误差的变化趋势均比较一致。调整过q-->oula的函数之后，神奇的误差消失了，发现主要原因是角度固定偏差。

两个方法放在一起

EKF的结果要更差

对比EKF与ESKF的结果发现，ESKF暂时并没有表现出比EKF更好的效果。

与组合导航过程进行对比

实际上组合导航的角度误差并没有很大，组合导航的观测更加丰富，运动学方程中考虑的量也更多。

组合导航中角度的误差大小

首先利用AHRS方法进行预先处理

可见误差变得比较大。

比较ESKF与AHRS的区别

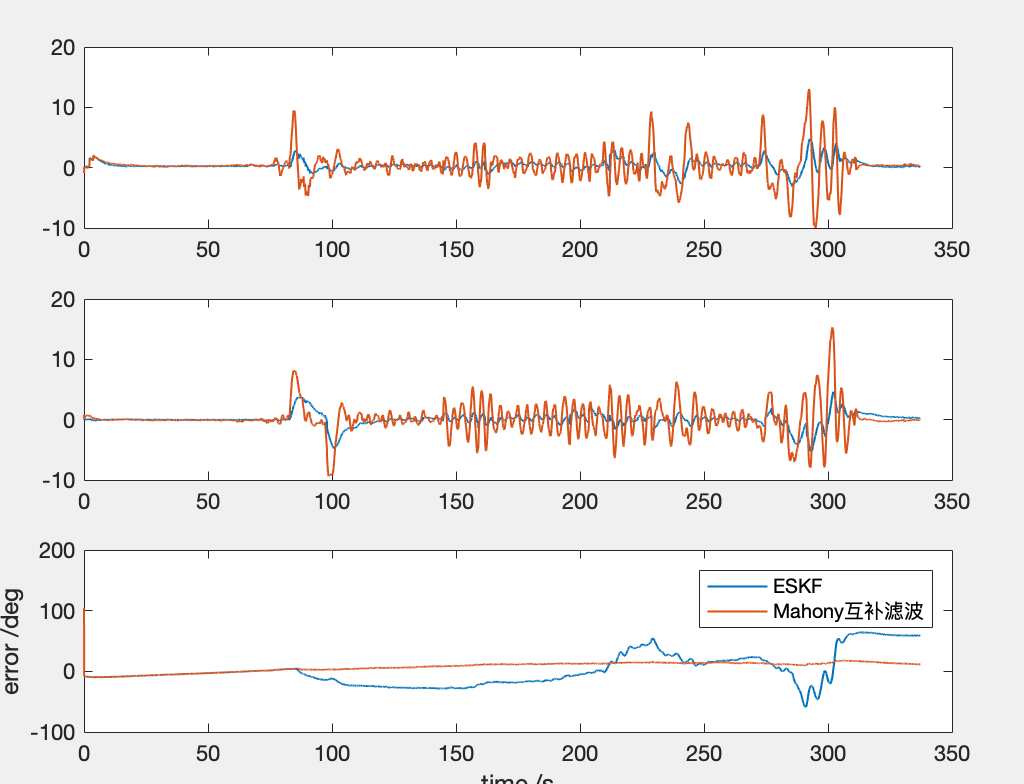
比例积分的AHRS与ESKF之间的对比

yaw角度区别不大，其余两轴的区别比较明显。

存在几个问题：

没有对加速度计的信号进行低通滤波（todo），不知道有什么意义？对于数据的预处理

梯度下降的AHRS与ESKF之间的对比

相比之下，ESKF的姿态角度估计的优势也并不明显。

结论部分

目前来看，error state的优势并不明显。

0629部分整理

ESKF没有地磁计

ESKF没有加上地磁计的测量量

可以发现，在没有地磁计的校准时，YAW角度的偏差比较大,bina

那么如果mahony互补滤波也缺乏地磁计的信号呢？

ESKF没有地磁，互补滤波没有地磁计

收到北航同学的博客启发，发现对于测量矩阵的雅可比矩阵有着更加简单的求导方法。

ESKF没有地磁计，并且换一种求H矩阵的方法

可以看到这样的误差相比上面是更大的。

Manhony也没有地磁计，并且计算测量雅可比矩阵时更换成R矩阵计算

可以见到互补滤波器的飘逸更加严重了。

这里的互补滤波器突然就飘到国外去了，可能是产生了奇异的问题。

四元数换成这种更新方式之后：

 det_q = [1;0.5*SamplePeriod*Gyroscope'];
 q = quatLeftComp(q)*det_q;
 Quaternion = q / norm(q); 
 Rwb = q2R(quaternion_l);
 Accelerometer = Accelerometer / norm(Accelerometer);    % normalise magnitude
 gra = [0;0;1];
 v = -Rwb'*gra;
 e = cross(Accelerometer, v);
 eInt_n = eInt + e * SamplePeriod;
 Gyroscope = Gyroscope + Kp * e + Ki * eInt_n;
 dotR = Exp_lee(Gyroscope*SamplePeriod);
 Rwb = Rwb*dotR;
 q = zeros(1,4);
 q = R2q(Rwb);
 Quaternion = q / norm(q);

减去eskf估计出来的偏差之后，得到这样的结果。

互补滤波将bias减去会不会表现好一点？

结果虽然不是很好，但是与之前的相差不大。

Mahony互补滤波最终最简单的形式为：

为什么这里的旋转矩阵变成Rbw？与我之前的逻辑都不太一样。

一个问题就是：

四元数的多种更新方法
四元数的更新方法要比旋转矩阵更加精确，可能是因为四元数比较容易归一化。

cacacadaxia/ESKF-Attitude-Estimation