I'm trying to build a simple model of the flight of the lesser house fly (Fannia canicularis).
During the summer months, I lie beneath a fabulous pendant lampshade (thank you IKEA) which is often the resting spot for a small number of flies doing their thing. And their thing is kind of cool. I have observed three distinct flight behaviours
- resting on the pendant lampshade
- a slow, square-like trajectory of approximately 40cm in width,
- and a rapid, more irregular "zooming" behaviour when near another fly.
Having noticed these distinct behaviours, I asked why they do this. And found that someone has documented the properties of the fly's flight, and talked about some of the reasons they do it. The 1986 paper includes some figures which I very much appreciated. And basically, I wanted to reproduce them.
Creating a simulation of lesser house flies lends its perfectly to agent-based modelling: where you give each fly (or agent) a prescribed list of behaviours, and see how they interact to create large-scale, emergent behaviours. Specifically, it might be interesting to see how the prescribed behaviours need to be defined in order to observe "zooming" at a similar frequency to real life.
Agent-based modelling is super cool. Watching animals flock and swoop and zoom is incredible and simple agent-based models have given insight into how emergent behaviours of large groups come about. Agent-based modelling has also been applied in cell biology to study morphogenesis, tumour growth and metastasis and formation of bacterial biofilms. These types of models (particularly as applied to morphogensis) are relevant to the work done in my PhD.
I think the ideal model would consist of multiple flies interacting in 3 dimensions, with all three behaviours. However, when building models I try to start simple and build up. So,
Iteration 1: 1 fly resting in 2 dimensions.
Iteration 2: 1 fly moving in a stright line. Also now in 3 spatial dimensions, with plots of xy and xz projections.
The plan for iteration 3 is to have the fly turn a corner (always either left or right only), hopefully moving in a square-like trajectory. Key steps for this iteration will be:
- to implement a 'turn' clock sampled from a Poisson distribution counting down the time until the fly turns, and
- to have the turning angle sampled from a gaussian distribution approximating 90 degrees in the xy plane.
Additional goals are to update the 'progress' animation to reduce the file size.
Here is a little gif showing progress so far:
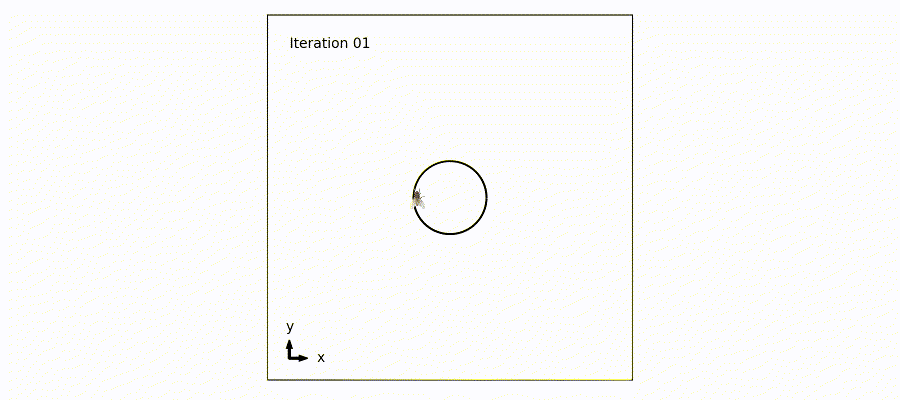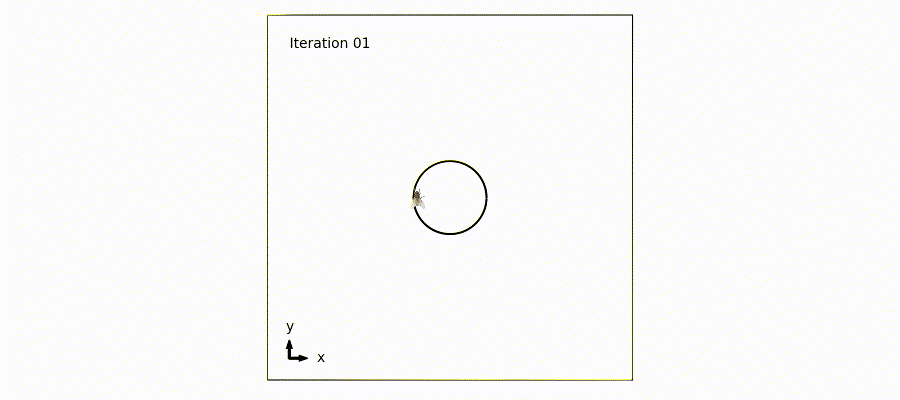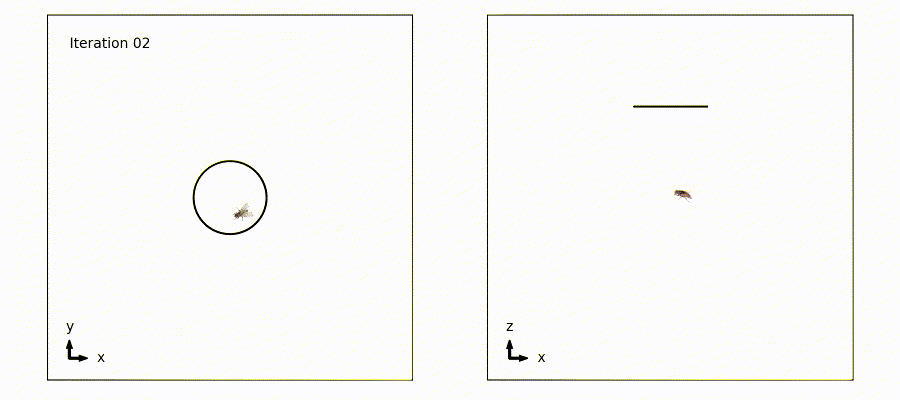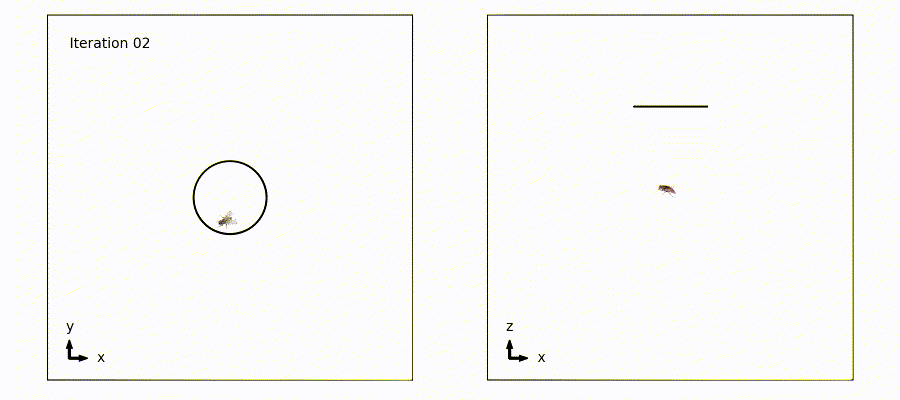
Figure reproduced from Jochen Zeil. (1986). The Territorial Flight of Male Houseflies (Fannia canicularis L.). Behavioral Ecology and Sociobiology, 19(3), 213–219. URL
Fly png images are downloaded from PNGWING.

