Cartesian Controllers

This package provides libraries with Cartesian ROS controllers.

It makes the following controller types available for the ROS-control framework:

for PositionJointInterfaces:
- position_controllers/CartesianMotionController
- position_controllers/CartesianComplianceController
- position_controllers/CartesianForceController
for VelocityJointInterfaces:
- velocity_interface/CartesianMotionController
- velocity_interface/CartesianComplianceController
- velocity_interface/CartesianForceController

Getting Started

Please see the README.md for each controller.

Features

All controllers rely on fast forward dynamics computations to circumvent the Inverse Kinematics problem. This dynamics-based solver is the same for all controller types and provides a consistent interface for configuration.

All controllers can handle robot chains with 1 to n joints. Note, however, that using less than 6 joints results in limited Cartesian responsiveness. For those systems, the controllers will try to get as close to minimizing the Cartesian error as possible, and as best as the robot kinematics allows for it.

With robot chains containing more than 6 joints, the controllers will move the additional elbows in an energy optimized manner.

The Control Loop

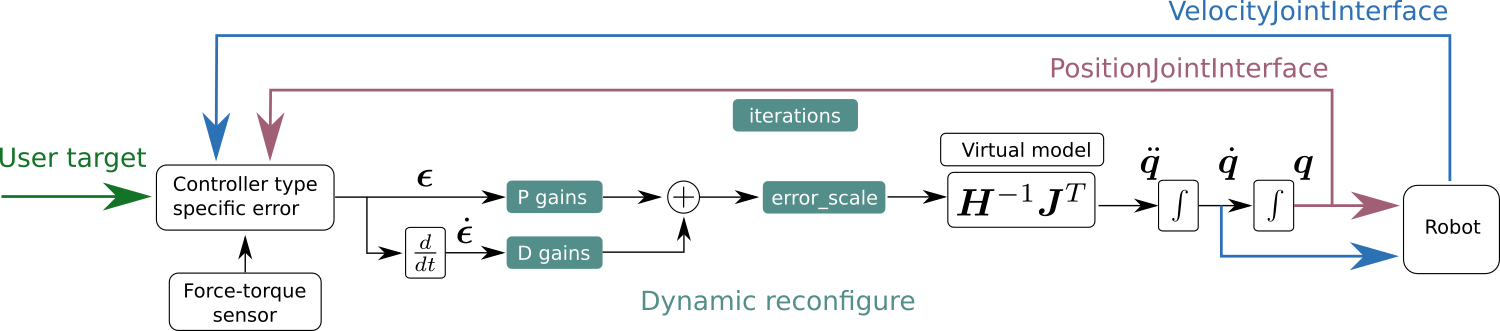
The above image depicts the general pipeline of the controllers. Users set specific targets, depending on their use case and the controller used. Each controller computes an error with respect to the current state. Users configure the responsiveness of the controller to that error with a set of gains. The error_scale is a convenient option to post-multiply the error on all dimensions uniformly. This is handy for testing parameter ranges with the slider in dynamic reconfigure. All controllers use the same virtual model to map this Cartesian error to joint accelerations, which is then double time integrated. There are two different mechanisms how those joint values get send to the robot. The joint position interface works in an open-loop manner, and allows for internal iterations, using feedback from the virtual robot model. The joint velocity interface takes the current robot state into account, and does not provide internal iterations.

Configuration

Controller gains

Forward dynamics turns the search for a feasible mapping of Cartesian input to joint space into a control problem. The solutions are found iteratively, whereby the system leaps forward in virtual time steps to reduce the Cartesian error. What this error is depends on the controller type used. For all controllers, a set of six PD gains (one for each Cartesian dimension) allows to tweak the responsiveness of the system with respect to this error.

Each controller README.md provides a set of meaningful default gains. Try starting with these values and continuously adapt those to your special use case.

Unfortunately, there won't exist ideal parameters for every use case and robot. So, for your specific application, you will be tweaking the PD gains at some point.

Solver parameters

The common solver has two parameters:

iterations: The number of forward simulated steps for each control cycle. Increasing this number will give the solver more iterations to decrease the error. However, this mostly makes sense for the CartesianMotionController, where increasing means switching from a smoothing controller to a fast and exact inverse kinematics solver.
error_scale: An additional multiplicative factor that uniformly scales the 6-dimensional PD controlled error (both translation and rotation alike). Use this parameter to find the right range for your PD gains. It's handy to use the slider in dynamic reconfigure for this.

Performance

As a default, please build the cartesian_controllers in release mode:

catkin_make -DCMAKE_BUILD_TYPE=Release

The forward dynamics implementation heavily relies on orocos_kinematics_dynamics (KDL), which use Eigen for linear algebra. Building in Release mode can give you a 10-times speed-up, and makes sure that the implementation of the control loop is not the performance bottle neck. If you use a higher number of iterations, then this in fact becomes a requirement.

cesar-vargas88/cartesian_controllers