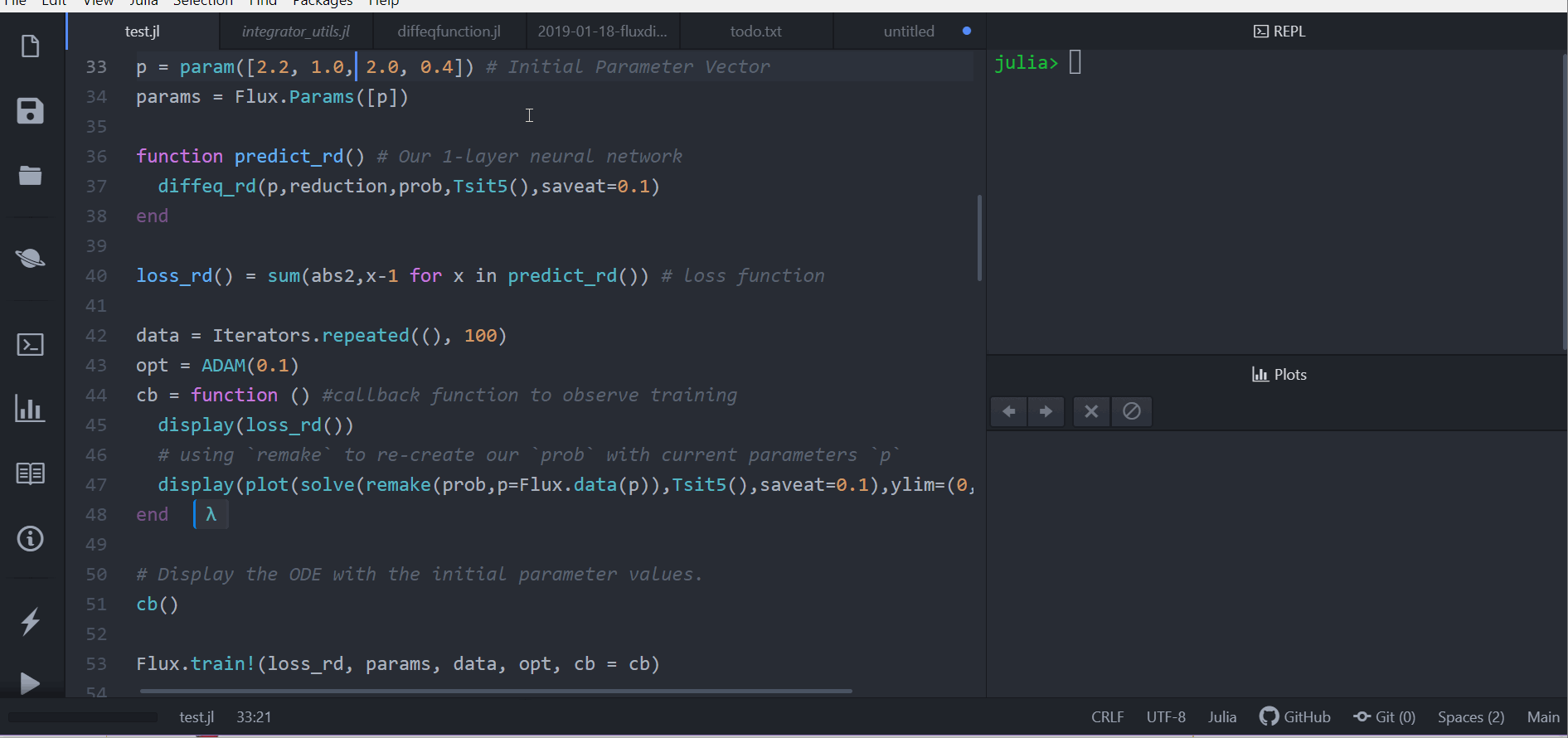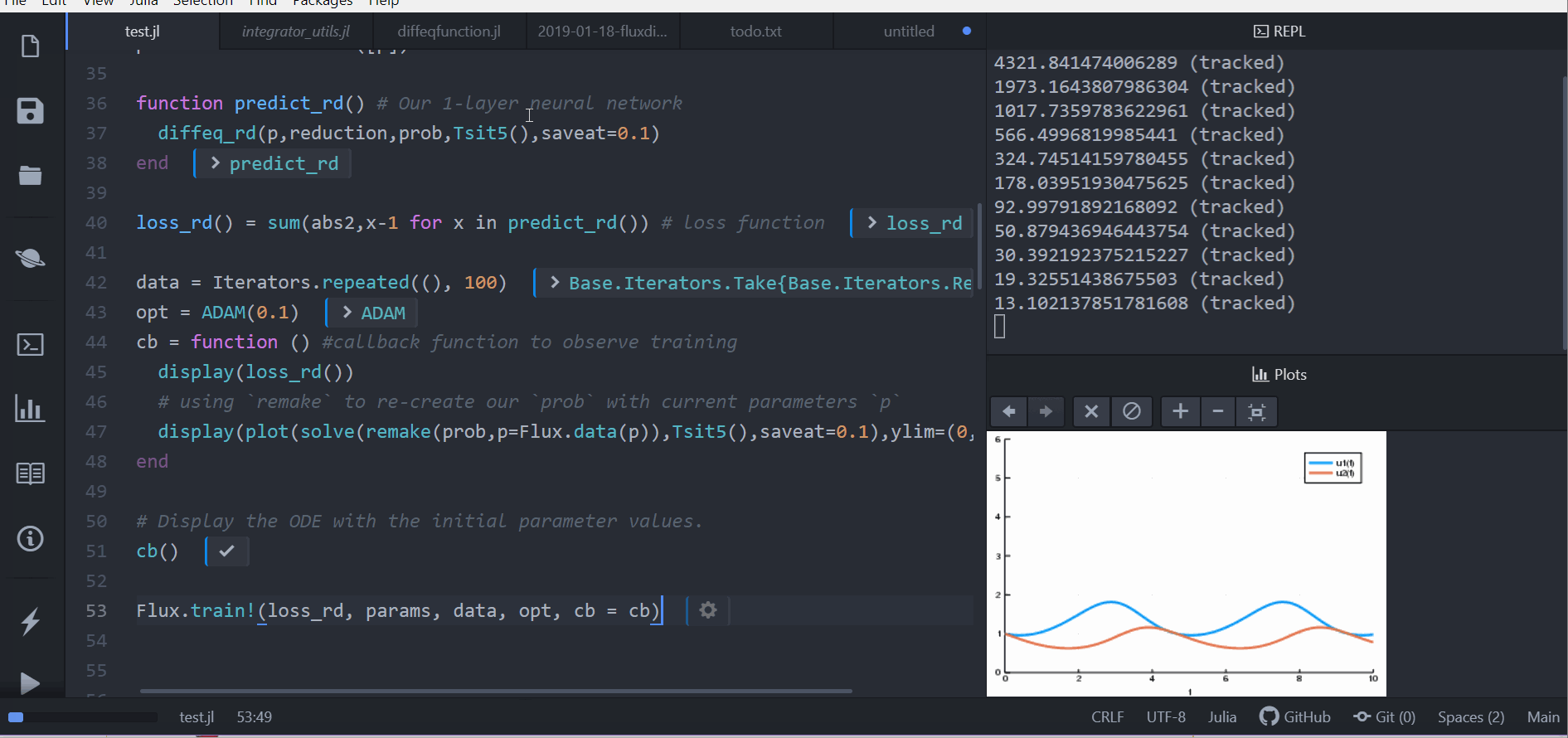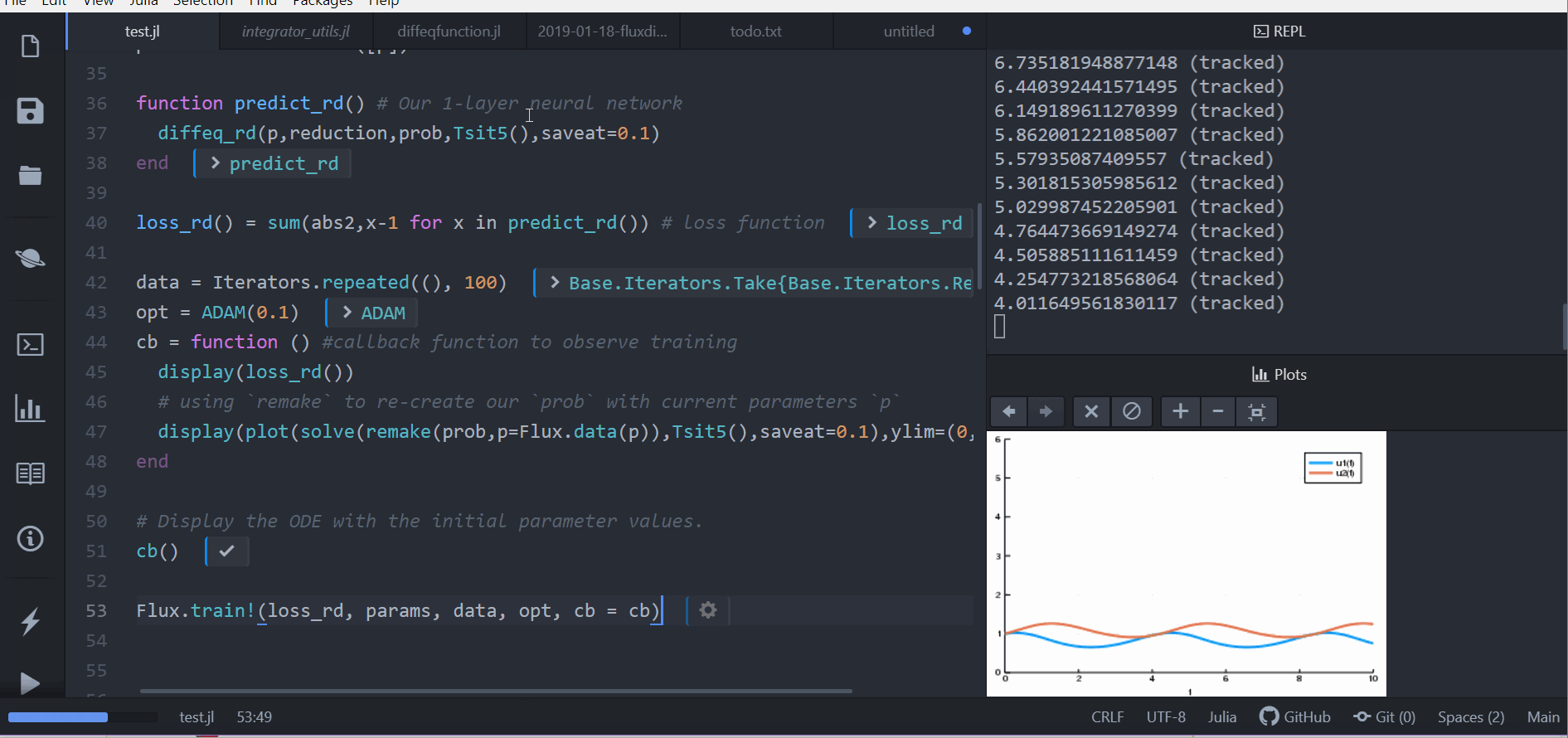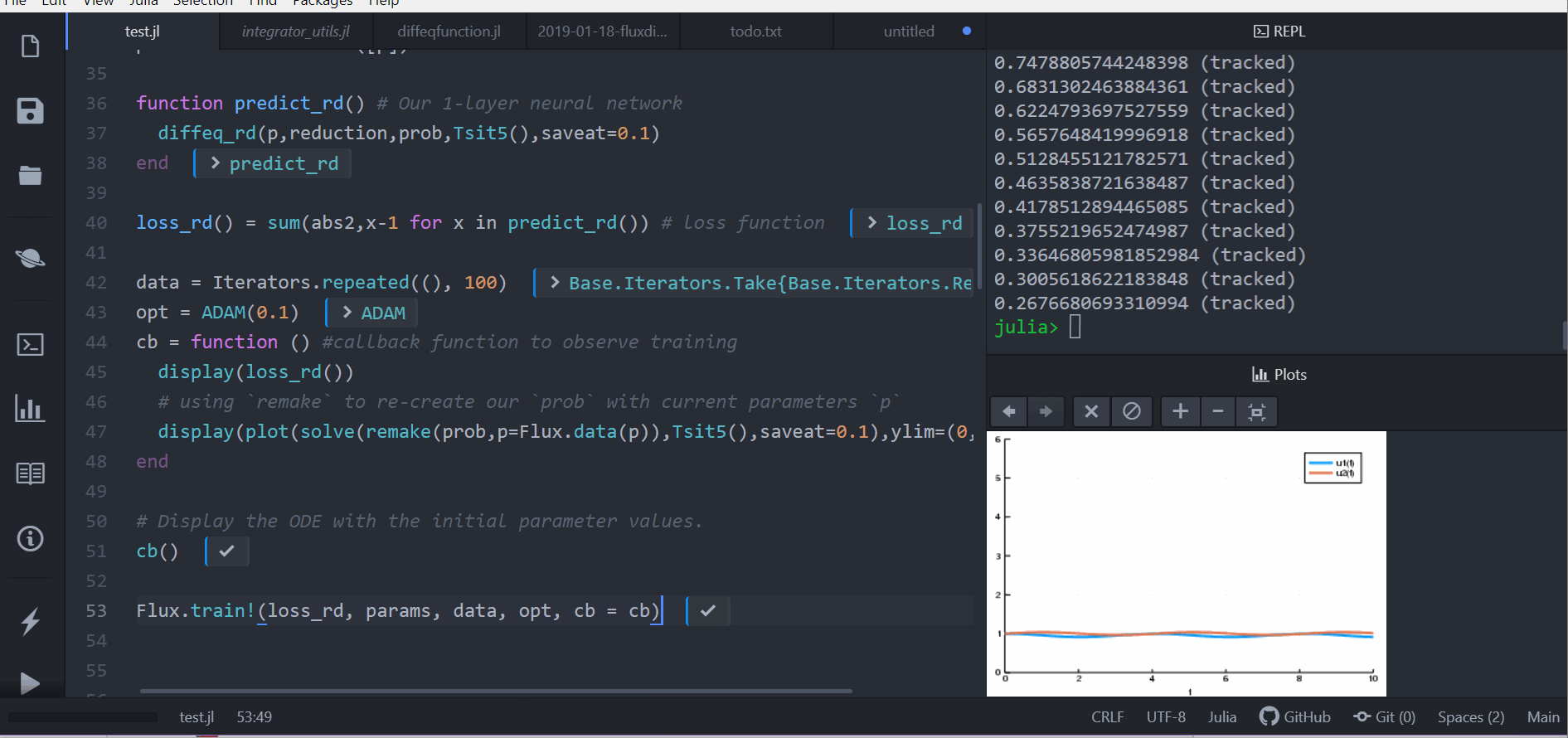
DiffEqFlux.jl fuses the world of differential equations with machine learning by helping users put diffeq solvers into neural networks. This package utilizes DifferentialEquations.jl and Flux.jl as its building blocks to support research in Scientific Machine Learning, specifically neural differential equations and universal differential equations, to add physical information into traditional machine learning.
For information on using the package, see the stable documentation. Use the in-development documentation for the version of the documentation which contains the un-released features.
DiffEqFlux.jl is not just for neural ordinary differential equations. DiffEqFlux.jl is for universal differential equations, where these can include delays, physical constraints, stochasticity, events, and all other kinds of interesting behavior that shows up in scientific simulations. Neural networks can be all or part of the model. They can be around the differential equation, in the cost function, or inside of the differential equation. Neural networks representing unknown portions of the model or functions can go anywhere you have uncertainty in the form of the scientific simulator. For an overview of the topic with applications, consult the paper Universal Differential Equations for Scientific Machine Learning.
As such, it is the first package to support and demonstrate:
- Stiff and non-stiff universal ordinary differential equations (universal ODEs)
- Universal stochastic differential equations (universal SDEs)
- Universal delay differential equations (universal DDEs)
- Universal partial differential equations (universal PDEs)
- Universal jump stochastic differential equations (universal jump diffusions)
- Hybrid universal differential equations (universal DEs with event handling)
with high order, adaptive, implicit, GPU-accelerated, Newton-Krylov, etc. methods. For examples, please refer to the release blog post. Additional demonstrations, like neural PDEs and neural jump SDEs, can be found at this blog post (among many others!).
Do not limit yourself to the current neuralization. With this package, you can explore various ways to integrate the two methodologies:
- Neural networks can be defined where the “activations” are nonlinear functions described by differential equations.
- Neural networks can be defined where some layers are ODE solves
- ODEs can be defined where some terms are neural networks
- Cost functions on ODEs can define neural networks