Xingyi Du, Danny M. Kaufman, Qingnan Zhou, Shahar Kovalsky, Yajie Yan, Noam Aigerman, Tao Ju
ACM Transaction on Graphics (Proceedings of SIGGRAPH Asia 2021)
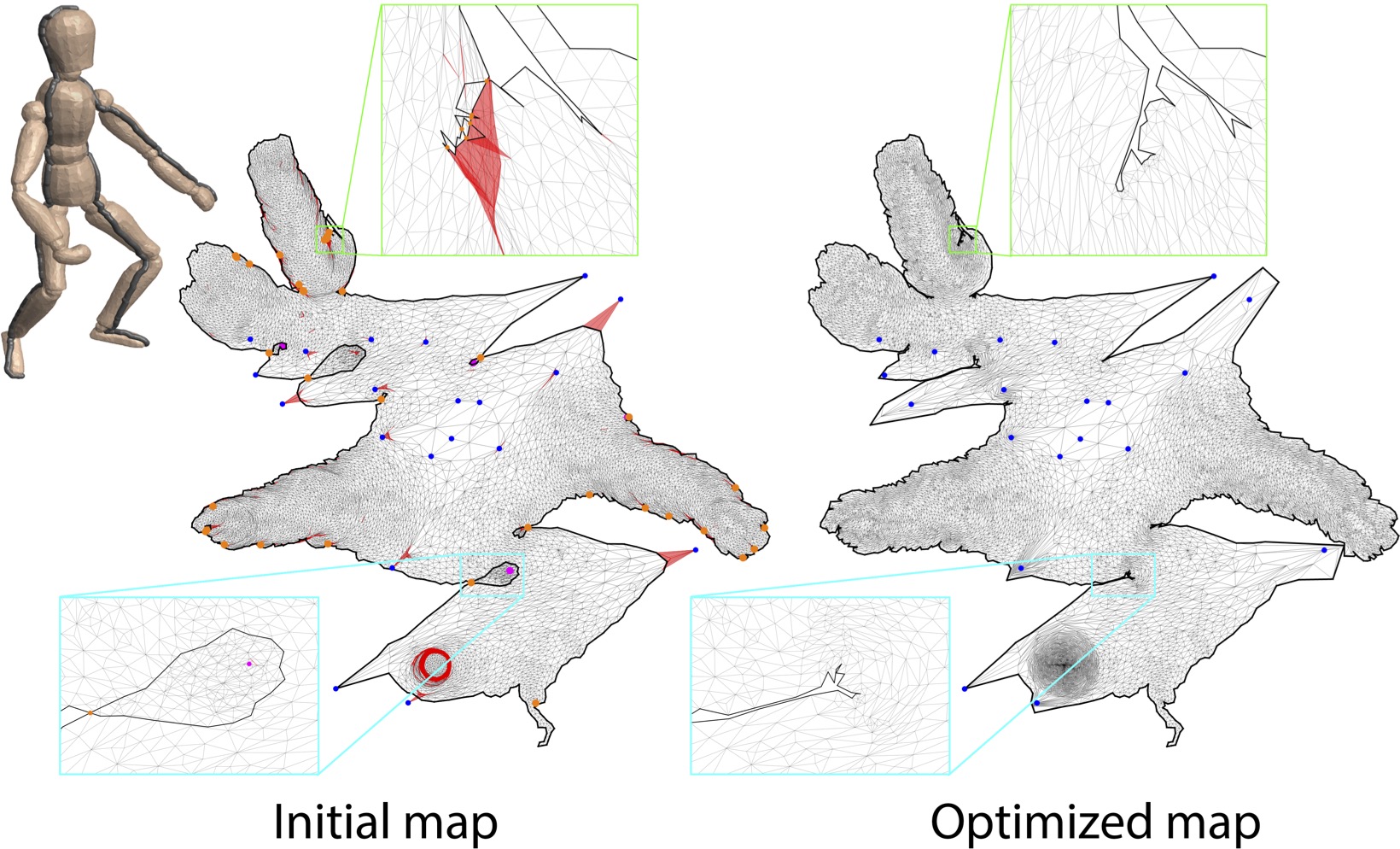
Injective parameterizations of triangulated meshes are critical across applications but remain challenging to compute. Existing algorithms to find injectivity either require initialization from an injective starting state, which is currently only possible without positional constraints, or else can only prevent triangle inversion, which is insufficient to ensure injectivity. Here we present, to our knowledge, the first algorithm for recovering a globally injective parameterization from an arbitrary non-injective initial mesh subject to stationary constraints. These initial meshes can be inverted, wound about interior vertices and/or overlapping. Our algorithm in turn enables globally injective mapping for meshes with arbitrary positional constraints. Our key contribution is a new energy, called smooth excess area (SEA), that measures non-injectivity in a map. This energy is well-defined across both injective and non-injective maps and is smooth almost everywhere, making it readily minimizable using standard gradient-based solvers starting from a non-injective initial state. Importantly, we show that maps minimizing SEA are guaranteed to be locally injective and almost globally injective, in the sense that the overlapping area can be made arbitrarily small. Analyzing SEA’s behavior over a new benchmark set designed to test injective mapping, we find that optimizing SEA successfully recovers globally injective maps for 85% of the benchmark and obtains locally injective maps for 90%. In contrast, state-of-the-art methods for removing triangle inversion obtain locally injective maps for less than 6% of the benchmark, and achieve global injectivity (largely by chance as prior methods are not designed to recover it) on less than 4%.
Here we release SEA-QN, a program that computes injective mapping under positional constraints by minimizing SEA (Smooth Excess Area) energy using quasi-Newton method.
The above figure illustrates what SEA does. It takes as input a source mesh, a group of positional constraints and a non-injective initial map, and outputs an injective map satisfying the positional constraints.
This program has been tested on macOS 12.0.1 (Apple Clang 13.0.0.13000029) and Windows 10 (Visual Studio Community 2022).
In terminal, navigate to our main directory, and run the following commands:
mkdir build
cd build
cmake -DCMAKE_BUILD_TYPE=Release ..
make -j
The program SEA_QN will be generated in the build subdirectory.
Open the folder containing CMakeLists.txt from visual studio. A cmake project will be configured and then you can build the program SEA_QN.exe in visual studio.
🔔 Important:
We use NLopt (version 2.7.0)'s L-BFGS quasi-Newton solver for optimization. This implementation doesn't track L-BFGS iterations, so it doesn't natively support the maxIteration termination criterion. To support this termination criterion, you need to replace the NLopt source file _deps/nlopt-src/src/algs/luksan/plis.c by the file plis.c we provide in the folder LBFGS_iteration_count. You need to rebuild the program for this change to take effect.
The executable SEA_QN asks for 3 arguments: path to an input data file, path to a solver options file, and path to the file to store the result.
./SEA_QN [input_file] [solver_options_file] [result_file]
An example is provided in the example subdirectory. Test it by:
./SEA_QN example/input example/solver_options example/my_result
The result will be written to example/my_result.
In the 3 arguments, input_file is mandatory, while the rest two are optional. If solver_options_file is not specified, SEA_QN will look for a file named solver_options in the same directory as the binary. If that file is not found, the program will fall back to default options. If result_file is not given, results will be written to a file named result in the directory of the binary.
Input file contains vertices and faces(i.e. triangles) information about the source mesh and initial embedding, as well as the indices of constrained vertices (called handles or positional constraints). Vertices are indexed from 0.
[num_sourceVert] [dimension_sourceVert]
... (num_sourceVert * dimension_sourceVert) Matrix ...
[num_initVert] [dimension_initVert]
... (num_initVert * dimension_initVert) Matrix ...
[num_simplex] [simplex_size]
... (num_simplex * simplex_size) Matrix ...
[num_handles]
... (num_handles * 1) Matrix ...
See example/input for a concrete example.
🎉 It's possible to use standard mesh formats. We provide a python script in directory IO to convert OBJ mesh formats to our input_file format.
To use the script, make sure to install meshio with
pip install meshio
To convert triangle meshes to our input format, run
./convert_input_2D.py [inputObjFile] [handleFile] [outFile]
Currently, we only support OBJ file with initial mesh as uv coordinates. Check out our dataset for some concrete OBJ and handle files. The handleFile contains a list of indices of constrainded vertices (indexed from 0).
The generated outFile will have the format of our input_file.
Solver options file contains parameters for SEA energy, options for NLopt solver, and a list of intermediate status to record during optimization.
form
[harmonic OR Tutte]
alphaRatio
[val]
alpha
[val]
theta
[val]
ftol_abs
[val]
ftol_rel
[val]
xtol_abs
[val]
xtol_rel
[val]
algorithm
[LBFGS]
maxeval
[val]
stopCode
[none OR no_flip_degenerate OR locally_injective OR globally_injective]
record
vert [0 OR 1]
energy [0 OR 1]
minArea [0 OR 1]
nbWindVert [0 OR 1]
grad [0 OR 1]
gradNorm [0 OR 1]
The following table explains each option in details. We recommend using the default values (especially "form", "alphaRatio", "alpha" and "theta") as they lead to high success rate in our experiments.
See example/solver_options for a concrete example.
| possible values | default value | explanation | |
|---|---|---|---|
| form | harmonic, Tutte | Tutte | two forms of SEA energy (see paper for details) |
| alphaRatio | [0, inf) | 1e-4 | Specify the ratio of content (area or volume) between rest mesh and target domain. Default value 1e-4 is recommended. |
| alpha | (-inf, inf) | -1 | If negative, alpha will be computed from alphaRatio. If non-negative, alpha will overwrite the value computed from alphaRatio. |
| theta | [0, 2Pi) | 0.1 | Specify the center angle of circular arcs replacing straight edges of the mesh boundary. (see paper for details) |
| ftol_abs | (-inf, inf) | 1e-9 | Absolute energy change stop threshold. Negative value means disabled. |
| ftol_rel | (-inf, inf) | 1e-9 | Relative energy change stop threshold. Negative value means disabled. |
| xtol_abs | (-inf, inf) | 1e-9 | Absolute variable change stop threshold. Negative value means disabled. |
| xtol_rel | (-inf, inf) | 1e-9 | Relative variable change stop threshold. Negative value means disabled. |
| algorithm | LBFGS | LBFGS | Quasi-Newton method. |
| maxeval | positive integer | 10000 | max number of iterations stop threshold. |
| stopCode | none, no_flip_degenerate, locally_injective, globally_injective | globally_injective | Custom stop criteria. "globally_injective": optimization will stop when the map becomes globally injective. |
| record:vert | 0, 1 | 0 | 1: record target mesh vertices at each iteration. |
| record:energy | 0, 1 | 0 | 1: record SEA energy at each iteration. |
| record:minArea | 0, 1 | 0 | 1: record smallest simplex signed content (area or volume) at each iteration. |
| record:nbWindVert | 0, 1 | 0 | 1: record number of overwound vertices at each iteration. |
| record:grad | 0, 1 | 0 | 1: record gradient at each iteration. |
| record:gradNorm | 0, 1 | 0 | 1: record the norm of gradient at each iteration. |
Result file stores the vertices of result mesh, and also intermediate records as specified in solver options file.
name dims
data
...
See example/result for a concrete example.
We provide a script to convert a result_file to a mesh file in directory IO.
Usage
./get_result_mesh.py [inputFile] [resultFile] [outFile]
For example,
./get_result_mesh.py example/input example/result result.obj
We release the benchmark dataset used to evaluate our method and compare with existing methods. The dataset includes 1791 triangular mesh examples. Each example includes a source mesh, up to 20 positional constraints, and a non-injective initial mesh generated by ARAP method. The dataset comes with both inputs and results of our method.