In the State Estimation Project,I have implemented a losely coupled estimator using Error-State Extended Kalman Filter (ES-EKF) to localize a Self Driving vehicle using a data set gathered during a test drive in the CARLA simulator.The data set contains measurements from a sensor array on a moving self-driving car.The sensor array consists of an IMU, a GNSS receiver, and a LiDAR, all of which provide measurements of varying reliability and at different rates.While driving, the vehicle is subject to various dynamic effects caused by the environment, the drive terrain, and the suspension.
The filter relies on IMU data to propagate the state forward in time, and GPS and LIDAR position updates to correct the state estimate A 10-dimensional state vector that includes a 3D position, a 3D velocity, and a 4D unit quaternion that will represent the orientation of our vehicle with respect to a navigation frame is used as the state of the vehicle and the IMU output specific forces and rotational rates in the sensor frame are taken as the inputs.
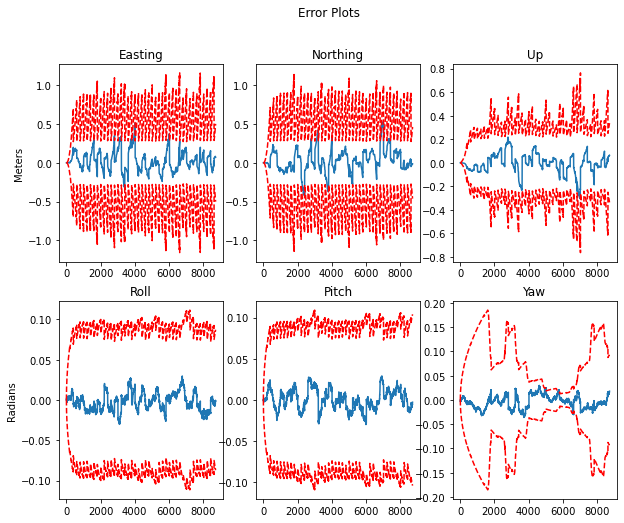
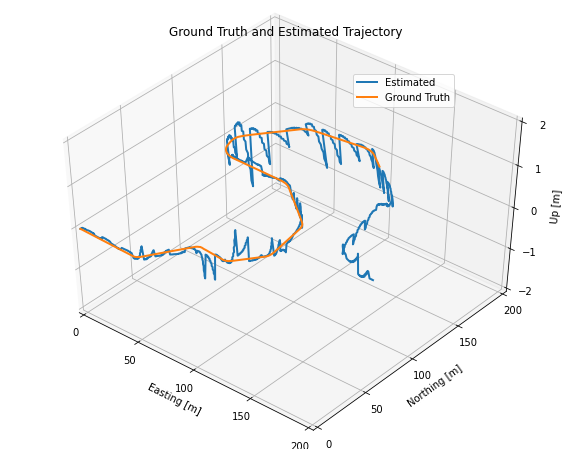
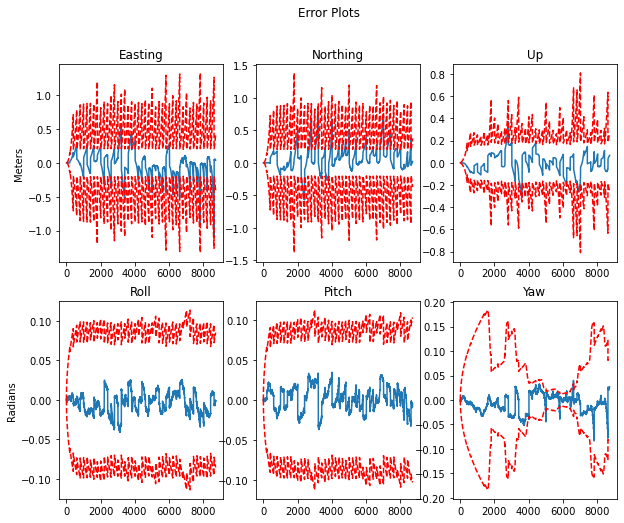
The LIDAR data is actually just a set of positions estimated from a separate scan-matching system, so we can insert it into our solver as another position measurement, just as we do for GNSS. However, the LIDAR frame is not the same as the frame shared by the IMU and the GNSS. To remedy this, we transform the LIDAR data to the IMU frame using our known extrinsic calibration rotation matrix and translation vector. To examine the effects, the transformation between the LIDAR sensor frame and the IMU sensor frame was intentionaly altered. This incorrect transform will result in errors in the vehicle position estimates.
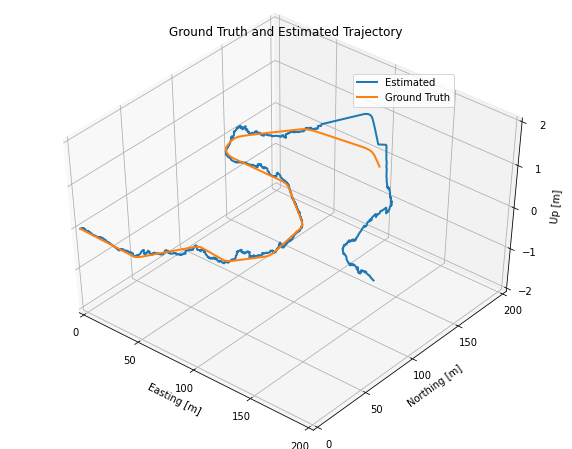
The error occurs in vehicle position estimate due to poor sensor calibration can be compensated by carefully tuning the filter parameters. The below results show the estimation obtained by tuning the sensor input noise variances for the LiDAR and the GNSS inputs to compensate the sensor miscalibration.
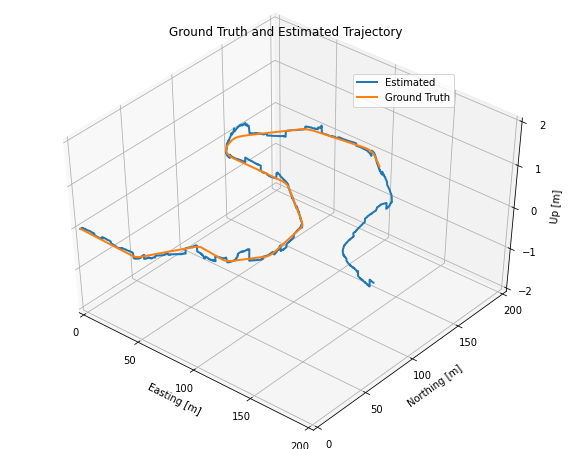
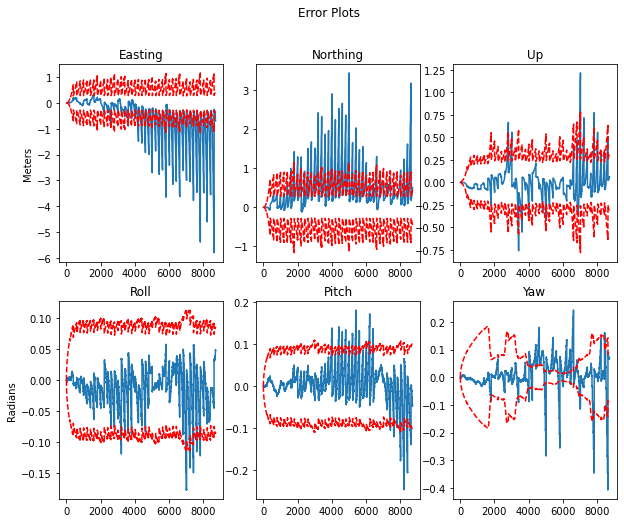
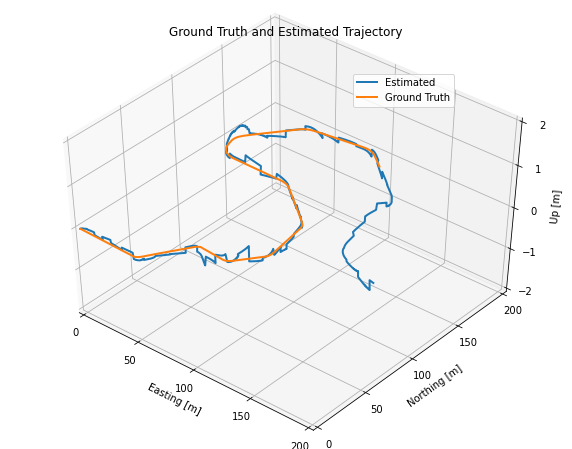
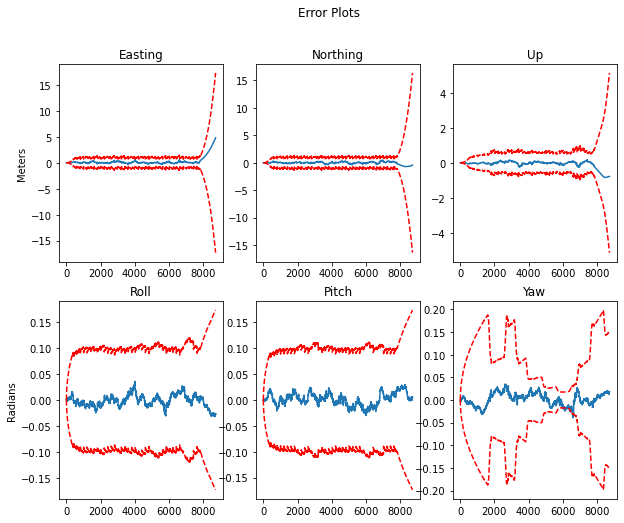
In Part 3, you will explore the effects of sensor dropout, that is, when all external positioning information (from GPS and LIDAR) is lost for a short period of time. For Part 3, you will load a different dataset where a portion of the GPS and LIDAR measurements are missing (see the detailed instructions below). The goal of Part 3 is to illustrate how the loss of external corrections results in drift in the vehicle position estimate, and also to aid in understanding how the uncertainty in the position estimate changes when sensor measurements are unavailable.
Examined the estimator output when all the external positioning information (from GPS and LIDAR) is lost for a short period of time to explore the effect of sensor dropout. the below results illustrate how the loss of external corrections results in drift in the vehicle position estimate and how the uncertainty in the position estimate changes when GNSS and LiDAR data are unavailable.
In Extended Kalman Filter Folder you may find the Extended Kalman Filter implemented in python to recursively estimate the position of a vehicle along a trajectory using available measurements and a motion model. The vehicle is equipped with a very simple type of LIDAR sensor, which returns range and bearing measurements corresponding to individual landmarks in the environment. The global positions of the landmarks are assumed to be known beforehand. We will also assume known data association, that is, which measurment belong to which landmark.
The vehicle motion model recieves linear and angular velocity odometry readings as inputs, and outputs the state (i.e., the 2D pose) of the vehicle The measurement model relates the current pose of the vehicle to the LIDAR range and bearing measurements.
State Estimation and Localization for Self Driving Cars by University of Toronto on Coursera
.png)