/Reinforcement-Learning-for-Decision-Making-in-self-driving-cars

Reinforcement-Learning-for-Decision-Making-in-self-driving-cars

Primary LanguagePython

Reinforcement Learning for Decision-Making for self-driving-cars

An practical implementation of RL algorithms for Decision-Making in Autonomous Driving
Related video: Introduction to the concepts of Markov Decision Process (MDP) and Reinforcement Learning (RL) with a focus on the applications for Autonomous Driving

Structure

My repository is structured as follow. Each time a main, an agent and an environment are required

  • src contains
    • environments
      • for now, only one simple environment is available
    • main_simple_road.py is the main for the simple_road environment
      • useful tools for vizualisation help to understand how each agent works
    • brains

Simple_road environment

A very basic scenario, but useful to apply and understand RL concepts. The envrionment is designed similarly to openai gym env

Use case

Environment definition:

  • Mission
    • The agent is driving on a straight road, while a pedestrian is standing on the pavement.
    • It has to reach the end of the road (the goal) with a certain velocity.

In addition, he must respect different constrains

  • apply traffic law
  • make sure to drive at a reduce speed when passing close to the pedestrian

Let's make the agent learn how to do that!

To visualize the progress of the driver at each episode, a tkinter-base animation can be used

  • The agent is depicted with a square
  • The colour of the square represents the velocity of the agent
  • The goal is depicted with a circle ("G")
  • The pedestrians on the side is represented with a black circle

Note1:

Note2: to disable the animation:

  • to disable the Tkinter window, set in flag_tkinter = False in main_simple_road.py
  • if you do not want to use Tkinter module, set the flag to False and uncomment the first line in the definition of the class Road in environments

Discrete State space:

  • the longitudinal position
  • the velocity The initial state is [0, 3]

Discrete Action space:

  • no_change - Maintain current speed
  • speed_up - Accelerate
  • speed_up_up - Hard Accelerate
  • slow_down - Decelerate
  • slow_down_down - Hard Decelerate

Reward Function: classified into 4 groups (See environments road_env.py)

  • time efficiency
  • traffic law
  • safety
  • comfort

Transition function: The transitions are based on the next velocity - e.g. if the Agent goes for velocity = 3, then its next position will be 3 cells further.

Termination Condition:

  • The task is episodic
  • One episode terminates after the Agent passed position = 18
  • In order to solve the environment, the agent must get an average return of +17 over 100 consecutive episodes.
    • Knowing that the maximum possible return is 18

Finally, hard constrains are used to eliminate certain undesirable behaviours

  • it is better to use action-masking rather than penalizing these behaviours in the reward function
  • it also increases the learning speed during training by limiting exploration

Dependencies

Create a conda environment: conda create --name rl-for-ad python=3.6

Install the packages: pip install -r requirements.txt

Using python 3 with following modules:

RL Agents

All the RL algorithms presented in these figures are implemented. Source

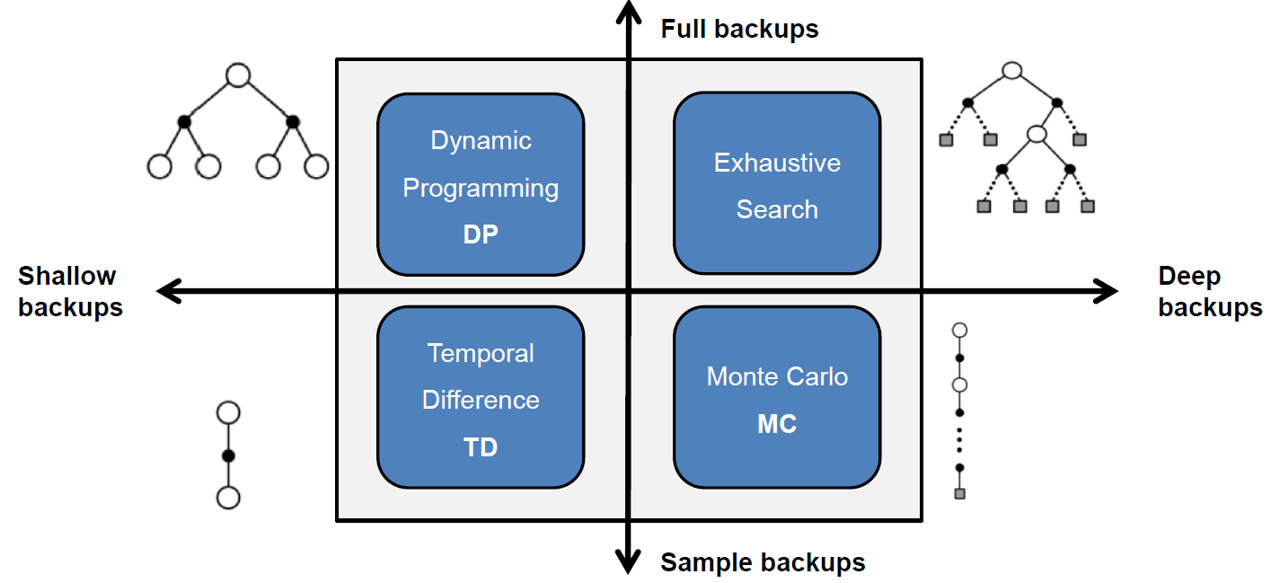DP-, MC-, and TD-backups are implemented
DP-, MC-, and TD-backups are implemented
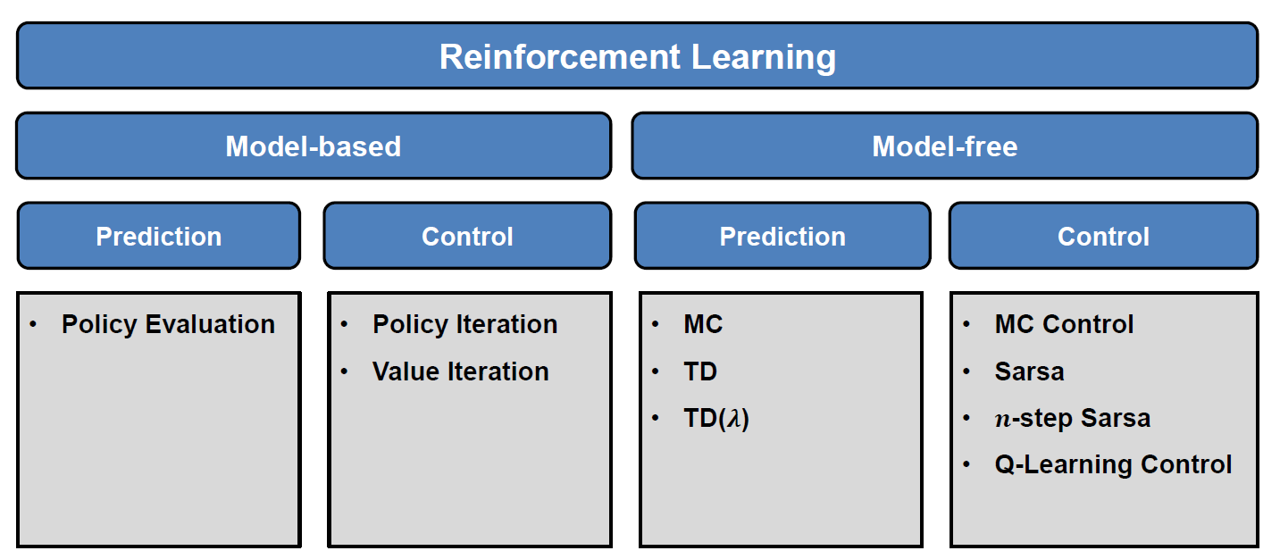Model-based and model-free Control methods are implemented
Model-based and model-free Control methods are implemented

Get Started

In src, main_simple_road.py is the central file you want to use.

Choose

  • the control Agent you want to use (uncomment the others)

    • Q-learning (= max-SARSA)
    • SARSA
    • SARSA-lambda
    • expected-SARSA
    • Monte-Carlo
    • Dynamic Programming

  • the task, playing with flags

    • training
    • testing
    • hyper-parameter tuning

  • if you want the environment window to be display

    • with the flag flag_tkinter = False for the simple environment

Results and Analysis:

Q-values

I tried different formats to store the q-values table:

Each one has its advantages and drawbacks.

The q-values are stored in a q-table that looks like:

[id][-------------------------actions---------------------------] [--state features--]
    no_change   speed_up  speed_up_up  slow_down  slow_down_down  position  velocity
0      -4.500  -4.500000       3.1441  -3.434166       -3.177462       0.0       0.0
1      -1.260  -1.260000       9.0490   0.000000        0.000000       2.0       2.0
2       0.396   0.000000       0.0000   0.000000        0.000000       4.0       2.0
3       2.178   0.000000       0.0000   0.000000        0.000000       6.0       2.0

Eligibility Trace for SARSA-Lambda

SARSA-Lambda updates the model by giving reward to all the steps that contribute to the end return. It can consider

  • One single step (SARSA) (lambda=0)
  • all the steps in the episode (Monte Carlo) (lambda=1)
  • in between (lambda in [0,1])

It is useful to vizualize the Eligibility Trace in the process of SARSA-Lambda. Here is an example of the lambda = 0.2 and gamma = 0.99 The id denotes the index of occurence: the smaller the index, the older the experience. The first experience has been seem 6 steps ago. Therefore, its trace is 1 * (lambda * gamma) ** 6 = 0.000060. The trace decay is high due to small value of lambda. For this reason, it is closer to SARSA rather than Monte Carlo.

[id][-------------------------actions---------------------------] [--state features--]
   no_change  speed_up  speed_up_up  slow_down  slow_down_down  position  velocity
0   0.000060  0.000000        0.000        0.0        0.000000       0.0       3.0
1   0.000000  0.000304        0.000        0.0        0.000000       3.0       3.0
2   0.001537  0.000000        0.000        0.0        0.000000       7.0       4.0
3   0.000000  0.000000        0.000        0.0        0.007762      11.0       4.0
4   0.000000  0.000000        0.000        0.0        0.039204      13.0       2.0
5   0.000000  0.000000        0.198        0.0        0.000000      13.0       0.0
6   0.000000  0.000000        1.000        0.0        0.000000      15.0       2.0
7   0.000000  0.000000        0.000        0.0        0.000000      19.0       4.0

Model-Based Control with Dynamic Programming

Optimal Policy and Value Function
Optimal Policy and Value Function

The Policy Iteration algorithm approximates the optimal Policy \pi*

Observations:

  • the pedestrian is located near position = 12
  • therefore the speed must be smaller than 3 when passing position = 12. Otherwise, an important negative reward is given.
  • the values of states that are close to position = 12 with velocity >= 4 are therfore very low. There is no chance for these state to slow down enough before passing the pedestrian. Hence, they cannot escape the high penalty.

I noticed that convergence of Policy Iteration is faster (~10 times) than Value Iteration

  • # Duration of Value Iteration = 114.28 - counter = 121 - delta_value_functions = 9.687738053543171e-06
  • # Duration of Policy Iteration = 12.44 - counter = 5 - delta_policy = 0.0 with theta = 1e-3 and final theta = 1e-5
  • In addition, on the figure it can be seen that Value Iteration suggests starting with action no_change whatever the initial velocity. This cannot be the optimal policy.

Optimal policy

Model-free and Model-based agents all propose trajectories that are close or equal to the optimal one. For instance the following episode (list of "state-action" pairs):

  • [[0, 3], 'no_change', [3, 3], 'no_change', [6, 3], 'no_change', [9, 3], 'slow_down', [11, 2], 'no_change', [13, 2], 'speed_up', [16, 3], 'no_change', [19, 3]]

Which makes sense:

  • the agent keeps his initial velocity
  • he slows down when approaching the pedestrian
  • he then speeds up to reach the goal with the required velocity

Hyper-parameters

It is possible to play with hyper-parameters and appreciate their impacts:

 hyper_parameters = (
            method_used,  # the control RL-method
            gamma_learning = 0.99,
            learning_rate_learning = 0.02,
            eps_start_learning = 1.0,
            eps_end_training = 0.02,
            eps_decay_training = 0.998466
        )
Epsilon-decay scheduling

I noticed that the decay rate of the epsilon has a substantial impact on the convergence and the performance of the model-free agents

I implemented an epsilon decay scheduling. At each episode: eps = max(eps_end, eps_decay * eps)

  • hence the value eps_end is reached at episode_id = log10(eps_end/eps_start) / log10(eps_decay)
  • in order to reach this plateau in episode_id episodes , eps_decay = (eps_end / eps_start) ** (1/episode_id)
  • I found that setting eps_decay_training = 0.998466 (i.e. 3000 episodes) helps converging to a robust solution for all model-free agents

Action-masking

I implemented the action_masking mechanism described in Simon Chauvin, "Hierarchical Decision-Making for Autonomous Driving"

It helps reducing exploration and it ensures safety.

This example of q-values for position = 1, when driving at maximal speed = 5, the agent is prevented from speed_up actions (q = -inf).

velocity   no_change  speed_up  speed_up_up  slow_down  slow_down_down
0  -3.444510 -0.892310    -0.493900       -inf            -inf
1   1.107690  1.506100     1.486100  -5.444510            -inf
2   3.506100  3.486100     2.782100  -0.892310       -7.444510
3   5.486100  4.782100         -inf   1.506100       -2.892310
4   6.782100      -inf         -inf   3.486100       -0.493900
5       -inf      -inf         -inf   4.782100        1.486100

Final value coherence checking

In the Bellman equation, if the episode is terminated, then q_target = r (next state has value 0)

  • Therefore, in the Optimal Value Function, the q-values of states that are just about to terminate is equal to the reward associated to the transition caused by the action.
  • I find it is very useful to monitor of such q-values in the learning process
Monitoring of the convergence of a given q-value
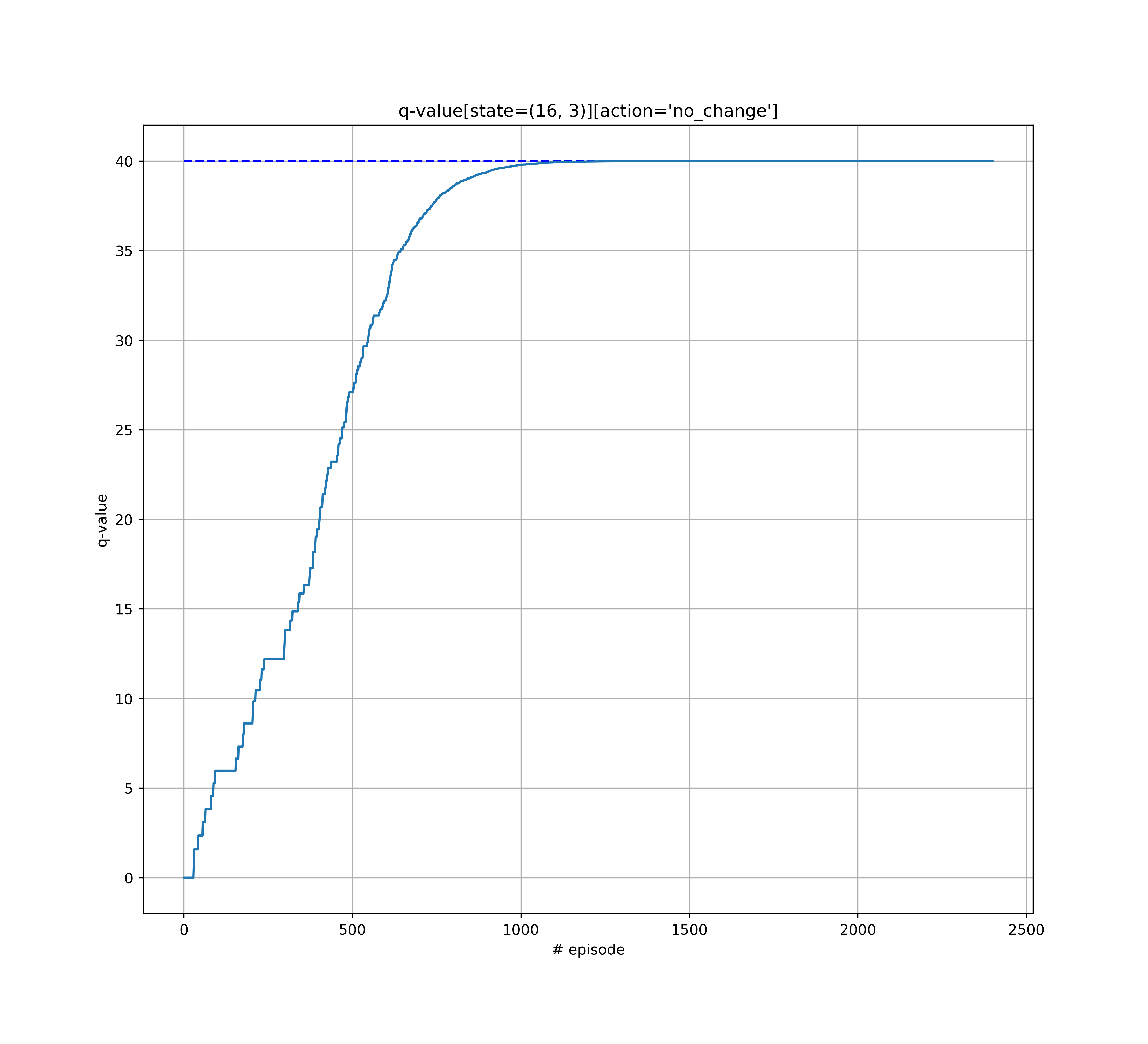Monitoring of the convergence of a given q-value

The q-value estimate for the state/action pair ([16, 3], "no_change") converges to the optimal value (+40 = reward[reach end with correct velocity])

Generated files

Overview of the parameters used for the environment

Weights of the Q-table

Plots in the training phase

Plots of the final Q-table

Best actions learnt by model-free agent after 4000 episodes
Best actions learnt by model-free agent after 4000 episodes
Due to the specification of the inital state, the model-free Agent cannot explore all the states.
Returns for each episode of a model-free agent
Returns for each episode, during the training of a model-free agent

The orange curve shows the average return over 100 consecutive episodes. It reaches the success threshold after 2400 episodes.

Example of settings

After training, env_configuration.json is generated to summarize the configuration.

{
  "min_velocity":0,
  "previous_action":null,
  "initial_state":[
    0,
    3,
    12
  ],
  "max_velocity_2":2,
  "state_ego_velocity":3,
  "obstacle1_coord":[
    12,
    2
  ],
  "actions_list":[
    "no_change",
    "speed_up",
    "speed_up_up",
    "slow_down",
    "slow_down_down"
  ],
  "goal_velocity":3,
  "goal_coord":[
    19,
    1
  ],
  "previous_state_position":0,
  "obstacle":null,
  "initial_position":[
    0,
    0
  ],
  "previous_state_velocity":3,
  "state_features":[
    "position",
    "velocity"
  ],
  "state_obstacle_position":12,
  "obstacle2_coord":[
    1,
    3
  ],
  "rewards_dict":{
    "goal_with_bad_velocity":-40,
    "negative_speed":-15,
    "under_speed":-15,
    "action_change":-2,
    "over_speed":-10,
    "over_speed_near_pedestrian":-40,
    "over_speed_2":-10,
    "per_step_cost":-3,
    "goal_with_good_velocity":40
  },
  "max_velocity_1":4,
  "max_velocity_pedestrian":2,
  "using_tkinter":false,
  "state_ego_position":0,
  "reward":0
}

Future Works

I am working on a more complex environment with a richer state space. Fine-tuning of hyper-parameter for DQN also belongs to the to-do list. Stay tuned!

Acknowledgments