partycls

partycls is a Python package for cluster analysis of systems of interacting particles. By grouping particles that share similar structural or dynamical properties, partycls enables rapid and unsupervised exploration of the system's relevant features. It provides descriptors suitable for applications in condensed matter physics, such as structural analysis of disordered or partially ordered materials, and integrates the necessary tools of unsupervised learning into a streamlined workflow.

Quick start

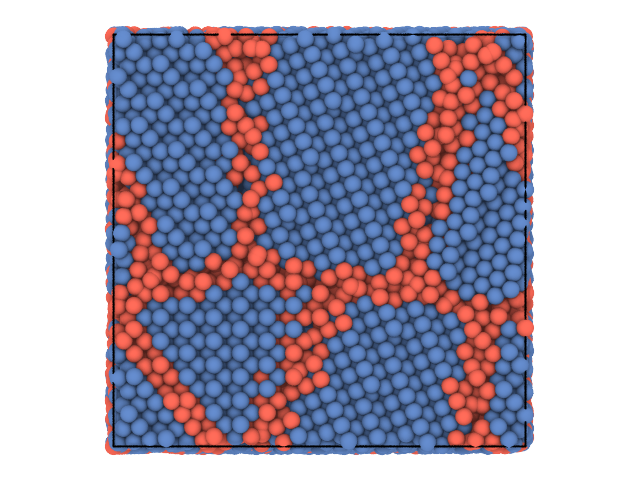
This quick example shows how to use partycls to identify grain boundaries in a polycrystalline system. The system configuration is stored in a XYZ trajectory file with a single frame. We use the local distribution of bond angles around each particle as a structural descriptor and perform a clustering using the K-Means algorithm.

from partycls import Trajectory, Workflow

traj = Trajectory('grains.xyz')
wf = Workflow(traj, descriptor='ba', clustering='kmeans')
wf.run()
traj[0].show(color='label', backend='ovito')

The results are also written to a set of files including a labeled trajectory file and additional information on the clustering results. The whole workflow can be tuned and customized, check out the tutorials to see how and for further examples.

Thanks to a flexible system of filters, partycls makes it easy to restrict the analysis to a given subset of particles based on arbitrary particle properties. Say we have a binary mixture composed of particles with types A and B, and we are only interested in analyzing the bond angles of B particles in a vertical slice:

from partycls import Trajectory
from partycls.descriptor import BondAngleDescriptor

traj = Trajectory('trajectory.xyz')
D = BondAngleDescriptor(traj)
D.add_filter("species == 'B'")
D.add_filter("x > 0.0")
D.add_filter("x < 1.0")
D.compute()

# Angular correlations for the selected particles
print(D.features)

We can then perform a clustering based on these structural features and ask for 3 clusters:

from partycls import KMeans

clustering = KMeans(n_clusters=3)
clustering.fit(D.features)
print('Cluster membership of the particles', clustering.labels)

Features

partycls accepts several trajectory formats (including custom ones) either through its built-in trajectory reader or via third-party packages, such as MDTraj and atooms.
partycls implements various structural descriptors: radial distribution, bond-angle distribution, standard bond order parameters (see the original paper), and locally averaged bond order parameters (see the original paper). On top of these native descriptors, partycls supports additional structural descriptors via DScribe.
partycls performs feature scaling, dimensionality reduction and cluster analysis using the scikit-learn package and additional built-in algorithms.

Requirements

numpy
scikit-learn
[optional] mdtraj (additional trajectory formats)
[optional] atooms < 3.0.0 (additional trajectory formats)
[optional] dscribe (additional descriptors)
[optional] matplotlib (visualization)
[optional] ovito (visualization)
[optional] py3Dmol (interactive 3D visualization)

Documentation

See the tutorials (Jupyter notebooks) for a step-by-step introduction to the main features of partycls and some of its applications.
Full API documentation.

Installation

1. From pypi:

pip install partycls

2. From the code repository:

git clone https://github.com/jorisparet/partycls.git
cd partycls
make install

Run the tests using:

make test

or manually compile the Fortran source and run the tests:

cd partycls/descriptor/
f2py -c -m realspace_wrap realspace.f90
cd ../../
pytest tests/

Support and contribution

If you wish to contribute or report an issue, feel free to contact us or to use the issue tracker and pull requests from the code repository.

We largely follow the GitHub flow to integrate community contributions. In essence:

fork the repository ;
create a feature branch from master ;
unleash your creativity ;
run the tests ;
open a pull request ;

We also welcome contributions from other platforms, such as GitLab instances. Just let us know where to find your feature branch.

Authors

Joris Paret

Daniele Coslovich: http://www-dft.ts.infn.it/~coslovich/

govarguz/partycls