Probability densities for exponentially-modified gaussian distributions
This function produces an unnormalized probability density function for the exGaussian distribution without serious numerical errors. It benefits from having the MATLAB Symbolic Toolbox installed.
This function wraps exgauss_pdf and normalizes the kernel.
It takes in a vector of sample points x and a 4-vector of parameters params.
The first parameter scales the entire kernel
(so for a normalized kernel, it should be unity).
The second parameter is the mean of the Gaussian.
The third parameter is the standard deviation of the Gaussian.
The fourth parameter is the time constant of the exponential
(a bigger parameter means a heavier tail).
For example:
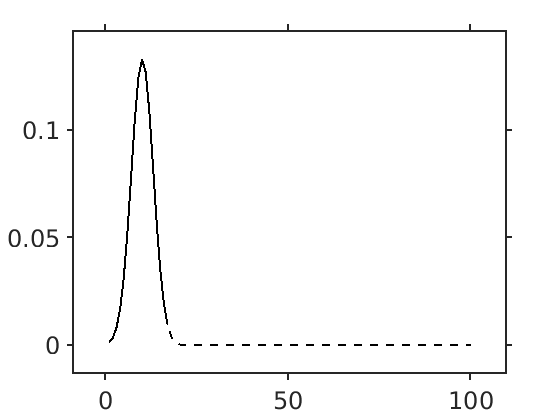
k = exgauss_kernel(0:100, [1, 10, 3, 0.1]);This function truncates a kernel after the mode of the distribution based on a cutoff parameter. Since kernels are often used for convolutions, the shorter a kernel is, the faster the computation will be. Thus, if a kernel has a very long tail with values close to zero, it is computationally efficient to truncate the tail, accepting a small amount of error in exchange for faster convolutions.
For example, to truncate a kernel to only values after the mode that are greater than 0.01:
truncated_kernel = truncate_kernel(kernel, 'Cutoff', 0.01);You can also renormalize the kernel like so:
truncated_kernel = truncate_kernel(kernel, 'Cutoff', 0.01, 'Normalize', true);Here, the kernel (dashed black line) and the truncated (cutoff = 0.01, solid black line) have been plotted on top of each other.