MPC control for the SpaceX Dragon spacecraft as it rendezvous with the ISS.

The ISS and the SpaceX Dragon spacecraft
The spacecraft is in circular orbit and its objective is to dock to the ISS. The simulation is implemented with a "sim to real gap" to account for unmodeled dynamics.
The MPC controller solves the following convex optimization problem :

Docking with the MPC controller
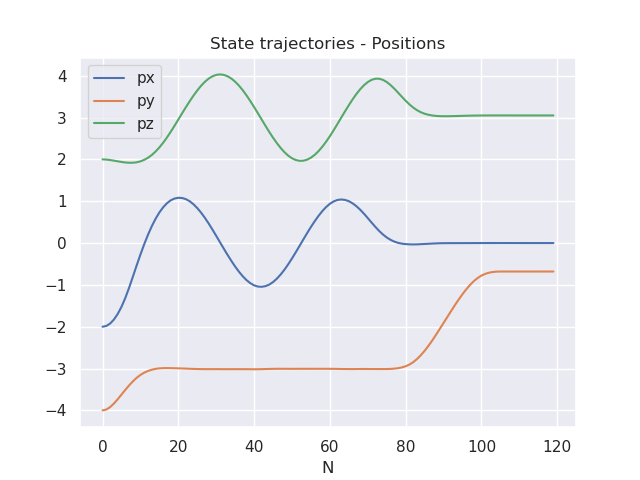
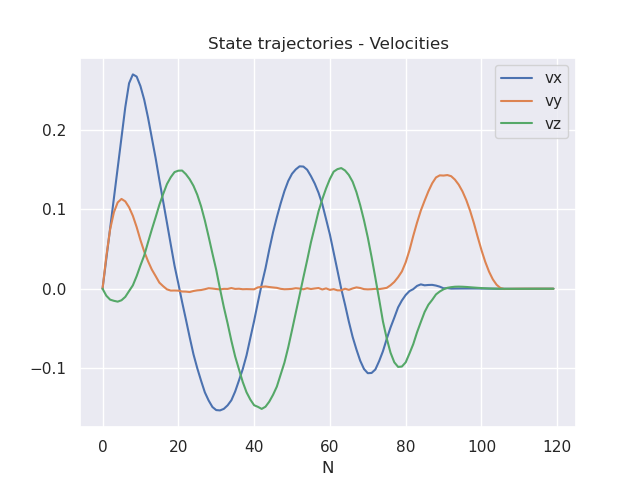
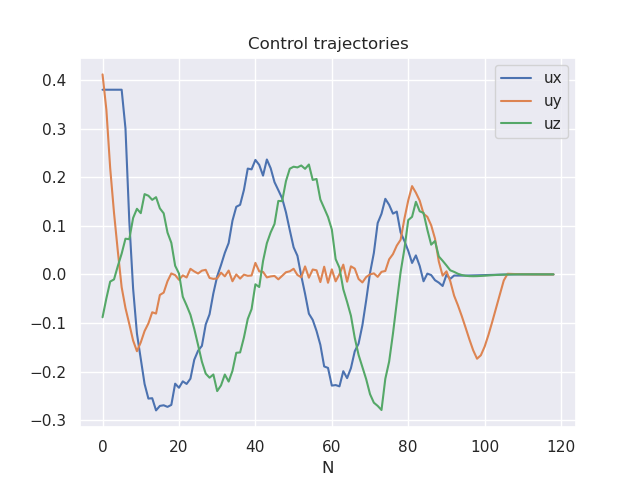
State and control trajectories:
The project was created with:
- Python 3.9.0
- numpy 1.24.2
- cvxpy 1.3.1
- matplotlib 3.6.2
- seaborn 0.12.2
- scipy 1.8.1
To use this project, install it locally via:
git clone https://github.com/elena-ecn/SpaceX-Dragon-mpc.git
The dependencies can be installed by running:
pip install -r requirements.txt
To execute the code, run:
python3 main.py