Tim-Oliver Buchholz1 and Florian Jug2
1tibuch@mpi-cbg.de, 2florian.jug@fht.org
Transformer architectures show spectacular performance on NLP tasks and have recently also been used for tasks such as image completion or image classification. Here we propose to use a sequential image representation, where each prefix of the complete sequence describes the whole image at reduced resolution. Using such Fourier Domain Encodings (FDEs), an auto-regressive image completion task is equivalent to predicting a higher resolution output given a low-resolution input. Additionally, we show that an encoder-decoder setup can be used to query arbitrary Fourier coefficients given a set of Fourier domain observations. We demonstrate the practicality of this approach in the context of computed tomography (CT) image reconstruction. In summary, we show that Fourier Image Transformer (FIT) can be used to solve relevant image analysis tasks in Fourier space, a domain inherently inaccessible to convolutional architectures.
Preprint: arXiv
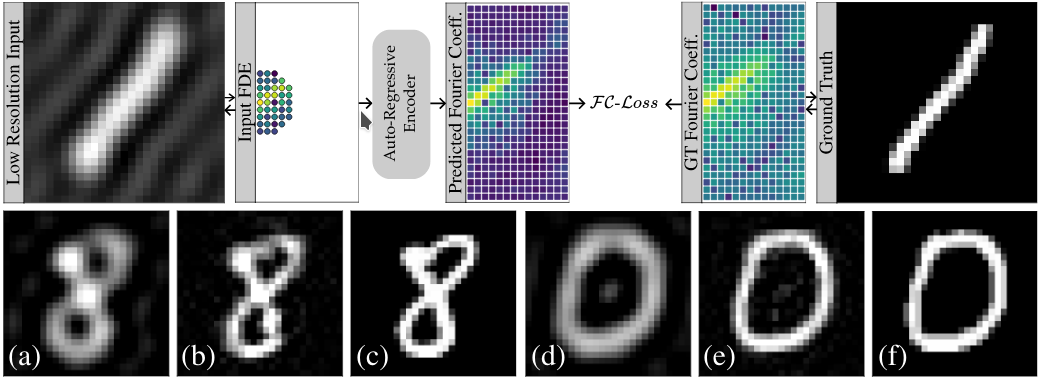
FIT for super-resolution. Low-resolution input images are first transformed into Fourier space and then unrolled into an FDE sequence, as described in Section 3.1 of the paper. This FDE sequence can now be fed to a FIT, that, conditioned on this input, extends the FDE sequence to represent a higher resolution image. This setup is trained using an FC-Loss that enforces consistency between predicted and ground truth Fourier coefficients. During inference, the FIT is conditioned on the first 39 entries of the FDE, corresponding to (a,d) 3x Fourier binned input images. Panels (b,e) show the inverse Fourier transform of the predicted output, and panels (c,f) depict the corresponding ground truth.
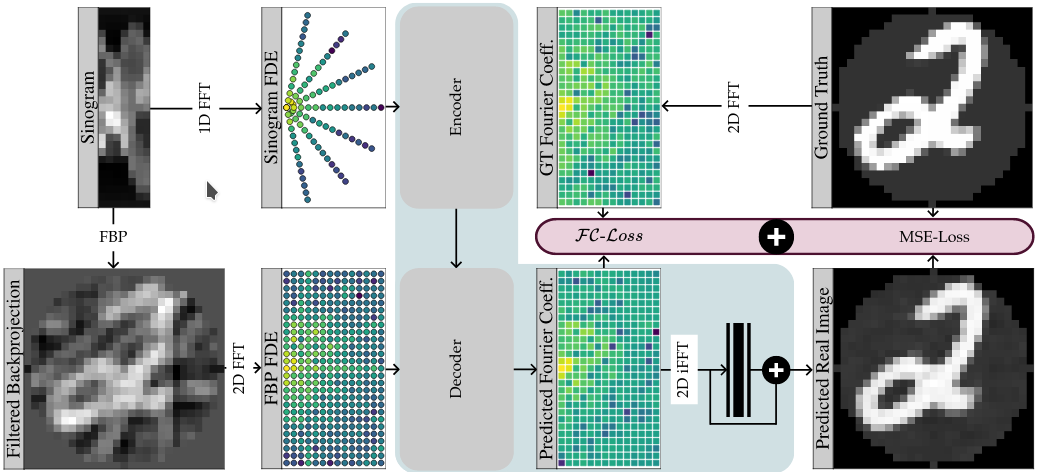
FIT for computed tomography. We propose an encoder-decoder based Fourier Image Transformer setup for tomographic reconstruction. In 2D computed tomography, 1D projections of an imaged sample (i.e. the columns of a sinogram) are back-transformed into a 2D image. A common method for this transformationis the filtered backprojection (FBP). Since each projection maps to a line of coefficients in 2D Fourier space, a limited number of projections in a sinogram leads to visible streaking artefacts due to missing/unobserved Fourier coefficients. The idea of our FIT setup is to encode all information of a given sinogram and use the decoder to predict missing Fourier coefficients. The reconstructed image is then computed via an inverse Fourier transform (iFFT) of these predictions. In order to reduce high frequency fluctuations in this result, we introduce a shallow conv-block after the iFFT (shown in black). We train this setup combining the FC-Loss, see Section 3.2 in the paper, and a conventional MSE-loss between prediction and ground truth.
We use fast-transformers as underlying transformer implementation. In our super-resolution experiments we use their
causal-linear implementation, which uses custom CUDA code (prediction works without this custom code). This code is
compiled during the installation of fast-transformers and it is necessary that CUDA and NVIDIA driver versions match.
For our experiments we used CUDA 10.2 and NVIDIA driver 440.118.02.
We recommend to install Fast Image Transformer into a new conda environment:
conda create -n fit python=3.9
Next activate the new environment.:
conda activate fit
Then we install PyTorch for CUDA 10.2:
conda install pytorch torchvision torchaudio cudatoolkit=10.2 -c pytorch
Followed by installing fast-transformers:
pip install --user pytorch-fast-transformers
Now we have to install the astra-toolbox:
conda install -c astra-toolbox/label/dev astra-toolbox
And finally we install Fourier Image Transformer:
pip install fourier-image-transformer
Start the jupyter server:
jupyter notebook
@misc{buchholz2021fourier,
title={Fourier Image Transformer},
author={Tim-Oliver Buchholz and Florian Jug},
year={2021},
eprint={2104.02555},
archivePrefix={arXiv},
primaryClass={cs.CV}
}