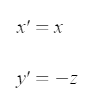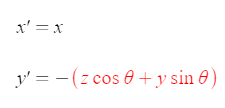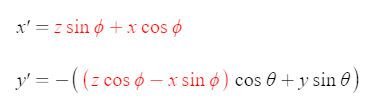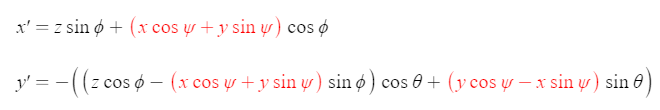for Rainmeter
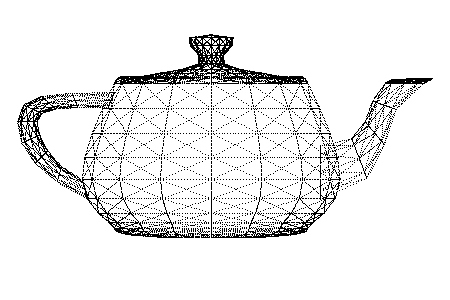
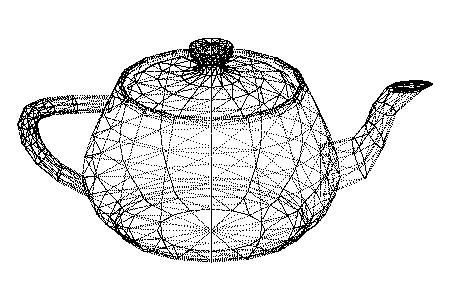
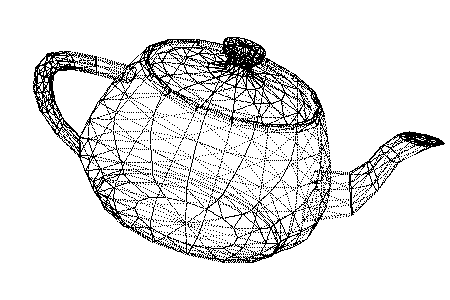
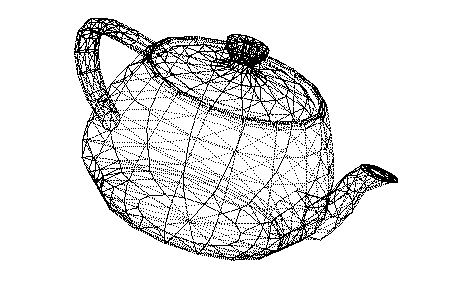
Renders 3D models as wireframes.
- Scale, rotate, and apply perspective to model
- Render vertices, edges, and/or faces
- Optional auto-rotation
- Automatically fits and centers model
- Uses no CPU while not being interacted with
- Supports STL and OBJ files
| Wireframe | Point Cloud | |
|---|---|---|
| Load time | None. | Many minutes or hours depending on model complexity. Once points are loaded, other models of equal or lesser complexity load instantly. |
| Render time | Slow. All but very low poly models have multi-second render times. However, even high complexity models render in less than 20 seconds. | Fast. Much more suited for animation, such as auto-rotation. |
| Render quality | High. Indistinguishable from actual 3D software. | Only renders vertices, so models with long straight edges may look strange. This can be slightly improved with edge interpolation. |
Hologram takes, for arbitrary points, 3D Cartesian coordinates (x, y, z) together with 3 angles of rotation (pitch, roll, yaw) and a perspective scalar, and translates them to screen space x and y.
Let's build its algorithm from the ground up.
Suppose you have an orthographic view of a set of points in 3D space such that the y-axis is parallel to your line of sight, with no rotation or perspective. In this situation, the y coordinates of the points do not matter.
As such, the translation of those coordinates to screen space is very simple.
We establish here that our viewport, for ease of implementation, is a square with the origin of the 3D space at its center. The x-axis of the viewport faces right and the y-axis faces down, as they do on your screen. The z-axis of the 3D space we are viewing faces up, so z coordinates must be flipped to compute screen space y coordinates.
Now we add pitch, which is rotation about the x-axis, or swivel up/down. This addition doesn't affect the x coordinate.
As pitch angle, θ (theta), increases from 0, the z coordinate will have less and less of an effect and the y coordinate will matter more and more. At 90°, or π/2 radians, the z coordinate won't matter, and the y coordinate has essentially replaced it.
There are mathematical tools that describe smooth oscillation between 1 and -1, through 0: sine and cosine.
We know to multiply the z coordinate by cosine of the pitch angle because at 0 degrees, it must be multiplied by 1. Similar logic follows for the y coordinate.
Roll, φ (phi), is rotation about y-axis, only, in this implementation, the y-axis of rotation itself is subject to the pitch angle. It works exactly like a gimbal.
This is where visualizing how this works in your head starts to get a little difficult. Fortunately, we aren't removing from or rearranging the formula at all, only adding to it.
This may be easier to picture if you imagine that the 3D object you are rotating is a uniform disc on the xz-plane. The uniformity of the disc means that it doesn't matter what its roll angle is, it will still look the same. Pitch remains the only meaningful rotation.
Now if you mark a dot on this disc whose pitch rotation we have already explained, the position of that dot will vary on the plane of the disc based on the effect of the roll angle on the x and z coordinates of the dot. At 0 roll angle, the dot's x coordinate is all that matters to screen space x, and the dot's z coordinate is all that matters to screen space y... thus we know where to apply sine and cosine.
Yaw, ψ (psi), is rotation about the z-axis. As you might guess, the z-axis of rotation is subject to the pitch and roll angles.
With two angles of rotation, we had to replace all instances of x and z coordinates, the coordinates that are affected by rotations about the y-axis of rotation. Now, with yaw, we must replace all instances of x (again) and y coordinates, as they are affected by rotations about the z-axis of rotation. The x coordinate is in both x' and y', and we replace it with the same thing in both places.
This requires calculating screen space z-depth, but all the work has already been done. The formula for z-depth is almost identical to the final formula for screen space y. All that changes is sin and cos θ.
This formula makes sense once you understand that if you rotated the starting angle for θ by 90°, screen space y would become z-depth. That is, in essence, what we are doing by changing cos θ to -sin θ and sin θ to cos θ, because sine and cosine are 90° offset from each other.
We then use it to obtain a value is greater than 1 if the point is closer to us than the origin, and less than 1 if it is farther, and use it to scale the final result.
This is not a true simulation of field of view (FOV). It merely approximates the effect by scaling up closer objects while shrinking far objects. perspective is a scalar used to control the strength of the FOV approximation. At 0, the effect is negated.
This isn't the only possible correct formula for 3D rotation. It is only correct for this set up, where the roll axis is specifically dependent on pitch, and the yaw axis is specifically dependent on both pitch and roll. For example, a different formula would be required for fixed axes of rotation. The formula would also change slightly depending on where you consider the zeroes of the rotation angles to be.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License.