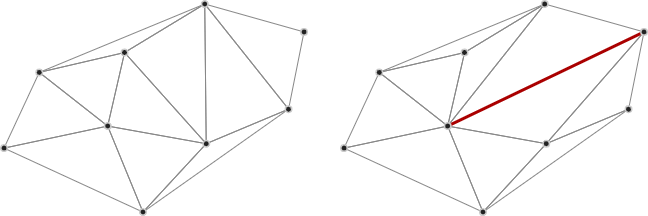
A library for constraining triangulations from Delaunator.
Constrainautor takes a Delaunay triangulation (from Delaunator), and turns it into a constrained (but not necessarily conforming) triangulation. You specify two points in the triangulation, and Constrainautor ensures there is an edge between those points.
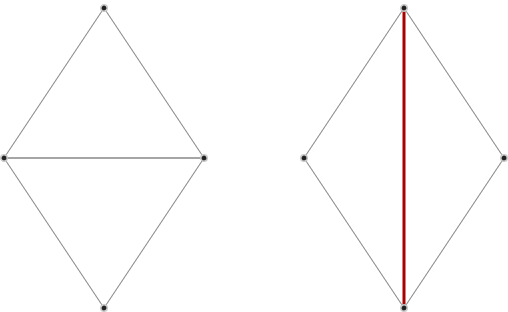
// A diamond
const points = [[150, 50], [50, 200], [150, 350], [250, 200]],
// Creates a horizontal edge in the middle
del = Delaunator.from(points),
con = new Constrainautor(del);
// .. but we want a vertical edge, from [150, 50] to [150, 350]:
con.constrainOne(0, 2);
// del now has the constrained triangulation, in the same format that
// Delaunator outputs
Install from NPM:
npm install @kninnug/constrainautor
Use in Node.js:
const Constrainautor = require('@kninnug/constrainautor');
or as an ECMAScript/ES6 module:
import Constrainautor from '@kninnug/constrainautor';
or in the browser:
<script src="node_modules/@kninnug/constrainautor/lib/Constrainautor.js"></script>
or minified:
<script src="node_modules/@kninnug/constrainautor/lib/Constrainautor.min.js"></script>
The Constrainautor library does not depend on Delaunator itself, but the input
is expected to be in the format that Delaunator outputs. The ES module variant
(lib/Constrainautor.mjs) depends on
robust-predicates, but the
CommonJS and minified versions (lib/Constrainautor.cjs and lib/Constrainautor.min.js)
come with this dependency compiled in, and can be used standalone. The (source)
TypeScript version is in Constrainautor.ts.
Besides being in the format that Delaunator outputs, the library has these other requirements on the input data:
- Points are not duplicated, i.e. no two points have the same x and y coordinates.
- No two constrained edges intersect with eachother.
- Constrained edges do not intersect with any point in the triangulation (beside their end-points).
- The outer edges of the triangulation form a convex hull.
- The triangulation has no holes.
The last two requirements are already guaranteed by Delaunator, but are important to keep in mind if you modify the triangulation before passing it to Constrainautor. If one or more of these requirements are not met, the library may throw an error during constrainment, or produce bogus results.
To triangulate a set of points, and constrain certain edges:
- Define the points to be triangulated:
points = [[x1, y1], [x2, y2], ...]. - Define the edges to be constrained:
edges = [[0, 1], [3, 4], ...]. These are indices into thepointsarray. - Generate a triangulation (using Delaunator):
del = Delaunator.from(points). - Make a constrainer:
con = new Constrainautor(del). Note thatdelwill be modified by the Constrainautor methods. - Constrain the triangulation:
for(const [p1, p2] of edges){ con.constrainOne(p1, p2); }.
Alternatively, you can call con.constrainAll(edges), which will constrain all
the edges in the supplied array. Or, (since version 4.0.0), call
new Constrainautor(del, edges) with the Delaunator output and the edges
array to create the Constrainautor and constrain the edges in one go.
You can then use the triangulation in del as described in the Delaunator
guide.
If you change the point coordinates and their triangulation (via Delaunator#update),
you need to re-constrain the edges by creating a new Constrainautor and going
through steps 3 - 5 again.
More details can be found in the comments of Constrainautor.ts.
Construct a new Constrainautor from the given triangulation. The del object
should be returned from Delaunator, and is modified in-place by the
Constrainautor methods. If edges is provided, it will constrain those with
constrainAll.
Constrain an edge in the triangulation. The arguments p1 and p2 must be
indices into the points array originally supplied to the Delaunator. It
returns the id of the half-edge that points from p1 to p2, or the negative
id of the half-edge that points from p2 to p1. Note: this half-edge id is
only valid up to the next call to constrainOne, after which the constrained
edge will still be there, but may have a different id.
Check non-constrained edges if they satisfy the Delaunay condition (for every
two triangles sharing an edge, neither lies completely within the circumcircle
of the other), and flip the edge if they don't. If deep is true, it will
check & correct until all flipped edges satisfy the condition, otherwise it will
do only one pass and some edges may still not be Delaunay.
NB 1: since version 4.0.0 it is no longer necessary (or useful) to call this
method after constraining edges, since constrainOne will also do it.
NB 2: since version 4.0.0 this method returns this instead of this.del.
A shortcut to constraining an array of edges by constrainOne. The argument
edges must be an array of arrays of indices into the points array originally
supplied to Delaunator, i.e: [[p1, p2], [p3, p4], ...]. Returns this.
NB: since version 4.0.0 this method returns the Constrainautor instance,
instead of the Delaunator object.
Whether the half-edge with the given id is a constraint edge. Returns true if
edg was earlier returned by a call to constrainOne. Note: this doesn't try
to detect if the edge must be a constraint, merely that it has been marked as
such by the Constrainautor instance.
Find the id of the half-edge going from p1 to p2. If there is only an edge
from p2 to p1 (i.e. it is on the hull), it will return the negated id. If
there is no edge between p1 and p2, the return value is Infinity.
The Delaunator object passed to the constructor and modified by constraining.
At construction time, the Constrainautor library allocates one Uint32Array, and two BitSet arrays, in addition to the arrays already present in the Delaunator output:
vertMap: a mapping of each point (vertex) in the triangulation to the (id of the) left-most edge that points to that vertex. This is used to find the edges connected to any given point.flips: keeps track of the edges that were flipped. It is used to determine which edges may need to be flipped again to restore the Delaunay condition.consd: keeps track of the edges that are constrained. It is used to ensure those edges are not flipped during re-Delaunifying.
(These should be considered private, and may disappear in a later version.)
During the constraining process, or the re-Delaunayfying, the library does no
dynamic allocations. Rather, it sets flips to 1 at the index of each edge that
was flipped, and iterates over this set afterwards to check the Delaunay
condition and flip the flipped edges again if needed.
The library uses robust geometric predicates from
robust-predicates and
robust-segment-intersect,
and should not break on smallish inputs. This can be changed by extending the
class and overriding the intersectSegments, inCircle, and isCollinear
methods. See the comments in Constrainautor.ts on how they should behave.
- Add
edgesparameter to constructor for one-shot constructing & constraining. - Change return value of
delaunifyandconstrainAllto return theConstrainautorinstance (the Delaunator output is still modified in place, and available atcon.del). - Fix issue #4 by
restoring the Delaunay condition immediately at the end of
constrainOne. Due to this, callingdelaunifymanually is no longer necessary. - Add
findEdgemethod. - Remove
fullparameter fromdelaunify: since calling it is no longer a necessity, when it is called, it will always check all edges. - Use 2 BitSets (see
BitSet.ts) for keeping track of the flips and constraints, instead of 1 flips array.
- Convert to TypeScript.
- Move built files to
lib/. - Add
fullparameter todelaunify. - Fix Delaunay condition-check in validators.
- Fix disappearing constraints.
- Fix delaunify not restoring the Delaunay condition for all changed triangle pairs.
- Move test files to separate repository (to share with other libraries).
- Add
isConstrainedconvenience method.
- Fix issue #2 by using robust-predicates.
- Remove
intersectSegments,inCircle, andsegPointDistSqfrom the API documentation.
- Add documentation for internal intersect methods, which can be overridden to fix robustness issues.
- Mitigate issue #2 by throwing when constraining segment leaves the hull.
- Add test files from Interesting Polygon Archive.
- Initial version
- The constraining algorithm is adapted from A fast algorithm for generating constrained Delaunay triangulations, 1992, S. W. Sloan.
- Uses Volodymyr Agafonkin's robust-predicates port of Jonathan Shewchuk's Adaptive Precision Floating-Point Arithmetic and Fast Robust Predicates for Computational Geometry.
- Robust segment-segment intersection test adapted from Mikola Lysenko's robust-segment-intersect.