Higher-order Spatial Impulse Response Rendering (HO-SIRR) is a rendering method, which can synthesise output loudspeaker array room impulse responses (RIRs) using input spherical harmonic (Ambisonic/B-Format) RIRs of arbitrary order. The method makes assumptions regarding the composition of the sound-field and extracts spatial parameters over time, which allows it to map the input to the output in an adaptive and more informed manner; when compared to linear methods such as Ambisonics.
The idea is that you then convolve a monophonic source with this loudspeaker array RIR, and it will be reproduced and exhibit all of the spatial characteristics of the captured space.
(Please note that the code is currently a "work in progress". Therefore, feedback is most welcome! :-)
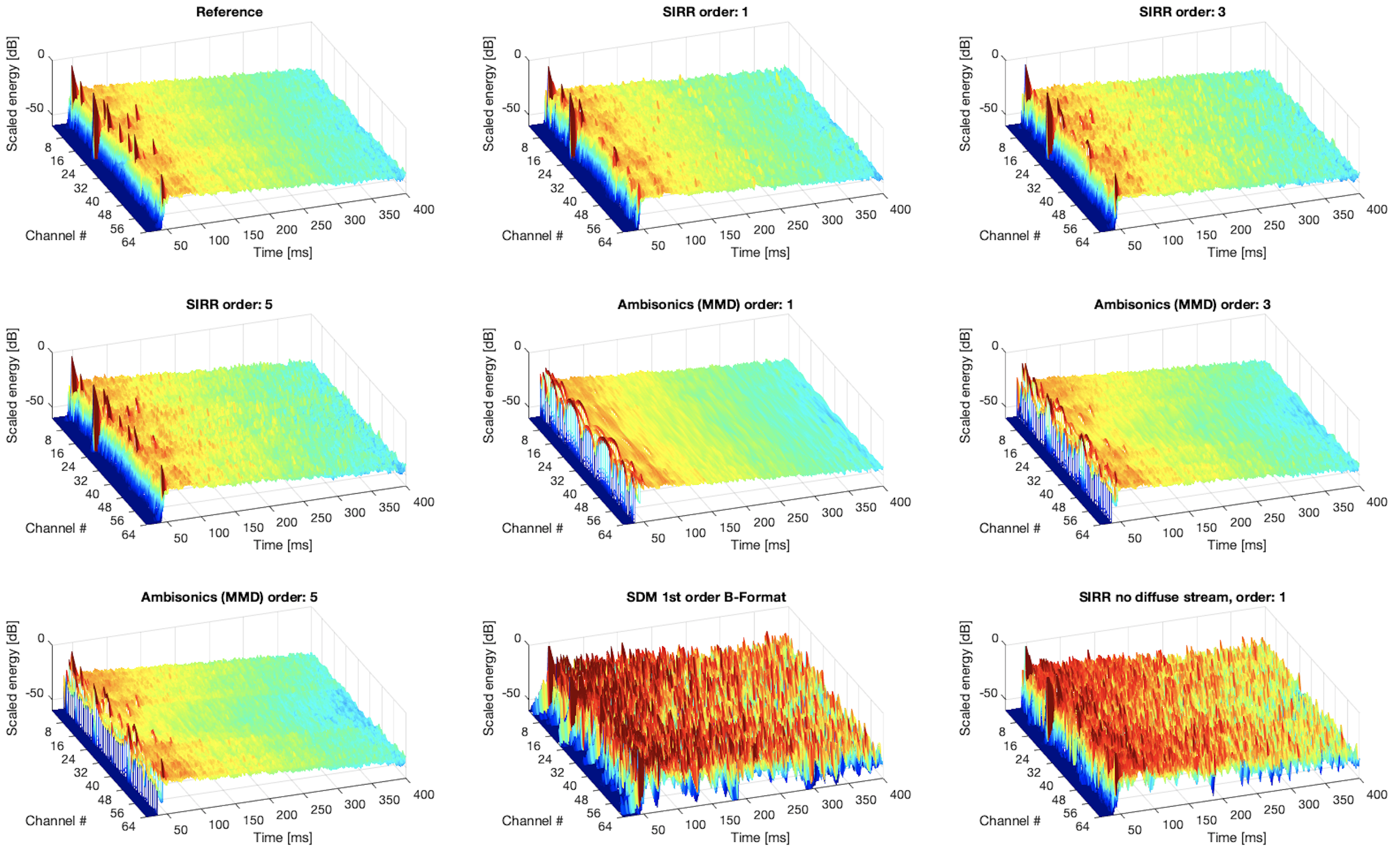
The above image depicts energy spectrograms of a 64-channel loudspeaker array RIR, rendered using different methods/configurations using the included 'plot_mch_energy.m' script. Here, it can be observed that the renderings using HO-SIRR more closely resembles the reference with increasing input order. It also performs visibly better than Ambisonics (MMD).
The code is reliant on the following Matlab libraries:
- Spherical-Harmonic-Transform
- Higher-Order-Ambisonics
- Vector-Base-Amplitude-Panning
- Array-Response-Simulator (Optional. Used in examples)
- SDM Toolbox (Optional. Used in examples)
The HO-SIRR script may be configured, for example, as:
pars.fs = 48e3;
pars.ls_dirs_deg = ???; % your loudspeaker array directions, [azi elev], in degrees
% Specify STFT windowing size in samples (note that HO-SIRR uses 50% window overlap)
pars.multires_winsize = [128];
pars.multires_xovers = [];
% OR: Specify windowing sizes for a multi-resolution STFT, for example:
% (512 up to 500Hz, then 128 up to 2kHz, then 64 above 2kHz)
%pars.multires_winsize = [512 128 64];
%pars.multires_xovers = [500 2e3];
% Diffuse rendering parameters
pars.RENDER_DIFFUSE = 1; % 0: disable diffuse rendering, 1: enable
pars.decorrelationType = 'noise'; % {'phase','noise'}, decorrelation via convolution with 'noise', or by randomising the 'phase'
pars.BROADBAND_DIFFUSENESS = 1; % 0: bin-wise estimation of diffuseness, 1: estimate diffuseness using broad-band intensity (<=maxDiffFreq_Hz)
pars.maxDiffFreq_Hz = 3e3; % frequency up to which to estimate the diffuseness parameter
pars.alpha_diff = 0.5; % diffuseness averaging coefficient (one-pole filter)
% Optionally, the highest peak of the response may be isolated and panned
% using a broad-band DoA estimate, which can reduce timbral colourations
% in some cases
pars.BROADBAND_FIRST_PEAK = 1; % 0: disabled, 1: enabled
The input Ambisonic RIR may then be rendered for your loudspeaker set-up as:
pars.chOrdering = 'ACN'; % 'ACN', or 'WXYZ'
pars.normScheme = 'N3D'; % 'N3D', or 'SN3D'
shir = audioread( ??? ) % load your input spherical harmonic RIR (of arbitrary order)
[lsir, lsir_ndiff, lsir_diff, pars, analysis] = HOSIRR(shir, pars);
% lsir - output loudspeaker impulse responses
% lsir_ndiff - output loudspeaker impulse responses, direct stream only
% lsir_diff - output loudspeaker impulse responses, diffuse stream only
% pars - output parameters
% analysis - analysed parameters stored during rendering
Then simply convolve this loudspeaker RIR (lsir) with a monophonic input stimulus, in order to reproduce it over your loudspeaker array and have it exhibit the spatial characteristics of the captured room.
- Leo McCormack - Matlab and algorithm design (contact: leo.mccormack@aalto.fi)
- Archontis Politis - Matlab and algorithm design
- Ville Pulkki - Matlab and algorithm design
This code is provided under the BSD 3-clause license.
[1] McCormack, L., Pulkki, V., Politis, A., Scheuregger, O. and Marschall, M., (2020). "Higher-Order Spatial Impulse Response Rendering: Investigating the Perceived Effects of Spherical Order, Dedicated Diffuse Rendering, and Frequency Resolution". Journal of the Audio Engineering Society, 68(5), pp.338-354.
[2] McCormack, L., Politis, A., Scheuregger, O., and Pulkki, V. (2019). "Higher-order processing of spatial impulse responses". In Proceedings of the 23rd International Congress on Acoustics, 9--13 September 2019 in Aachen, Germany.
[3] Politis, A. and Pulkki, V., 2016. "Acoustic intensity, energy-density and diffuseness estimation in a directionally-constrained region". arXiv preprint arXiv:1609.03409.
[4] Merimaa, J. and Pulkki, V., 2005. "Spatial impulse response rendering I: Analysis and synthesis". Journal of the Audio Engineering Society, 53(12), pp.1115-1127.
[5] Pulkki, V. and Merimaa, J., 2006. "Spatial impulse response rendering II: Reproduction of diffuse sound and listening tests". Journal of the Audio Engineering Society, 54(1/2), pp.3-20.
[6] Favrot, S. and Buchholz, J.M., 2010. "LoRA: A loudspeaker-based room auralization system. Acta Acustica united with Acustica", 96(2), pp.364-375.