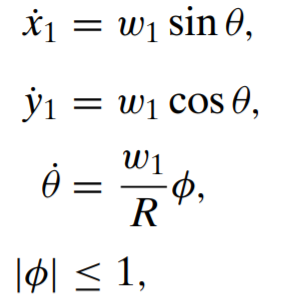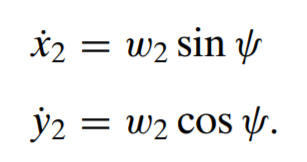Simulating differential games (specifically pursuit/evasion scenarios) using python.
Differential equations
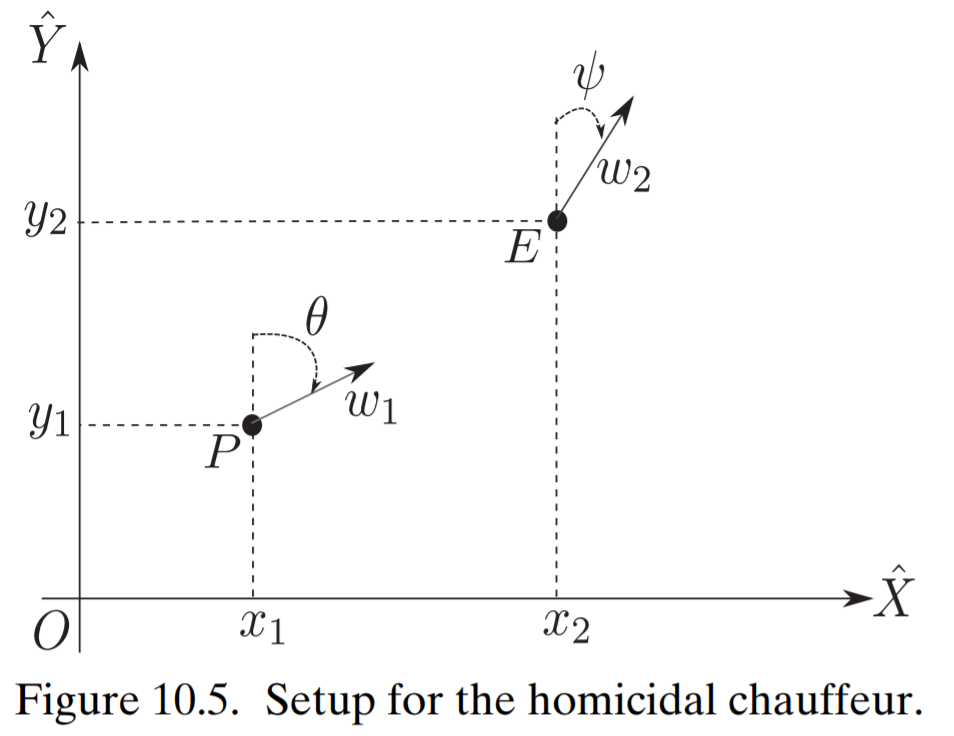
source: Fundamentals of Aerospace Navigation and Guidance by Kabamba & Girard
Differential equation solver
Python/Scipy solv_ivp
or could implement as a discrete time system...
Player strategy ideas (for choosing heading angles)
- Minimize/maximize distance
- Move in tangential direction of attacker
- Knowing previous history of other player or not
- Neural network / machine learning for creating strategy using sklearn libraries (maybe...)
Pursuer strategies
phiSingleState- calculates the requiredphito reach the evader using a single snapshot (issues witharctan2range wrap)phiThetaHistory- calculates the requiredphito reach the evader using previousthetahistory (solves thearctan2wrap issue)phiPerturb- simple method based onphiThetaHistorybut handles a detected loop by perturbing the pursuerphi
Evader strategies
psiRandom- random direction changes every 20 stepspsiTurn90- every 5 steps, calculates newpsithat is 90 degrees from a line drawn from pursuer to evader. Left vs right turn is handled depending on pursuer heading.
Current winning strategy: phiPerturb beats all pursuer methods
Caveat: this may be because of a flaw in the psiTurn90 algorithm
Algorithms
- Initialize with some set of parameters.
- Simulate first step using ODE solver.
- Choose heading angles using strategy.
- Repeat 2 and 3 until time runs our or collision occurs.
Notes
- wavy behavior exhibited when using
phiCalcSingleStateis solved usingnp.unwrapwith previous history inphiCalcThetaHistory- not sure if this is a bug or not: whenever the pursuer misses, it makes a loop.
- Running instructions (overall run with
python3 main.py):runAllSimruns all methods against each other and outputs resultsrunSimruns a specific methodanimate.animateallows for animated python figure
- To-Do: rewrite using object oriented programming