Is a pure Python package for simulating and calculating multistate dynamical process on networks. This work is based on a paper written by Peter G. Fennell and James P. Gleeson [1] where they introduced generalized approximation frameworks for the study and analysis of multistate dynamical processes on networks. They presented three degree-based frameworks, which allows to analyse the effects of network connectivity structures on dynamical processes. This work stands on fundamentals of stochastic processes [2] and network theory [3].
In this work we offer both empirical and analytical parts, therefore, we splitted the work into 4 fundamental objects:
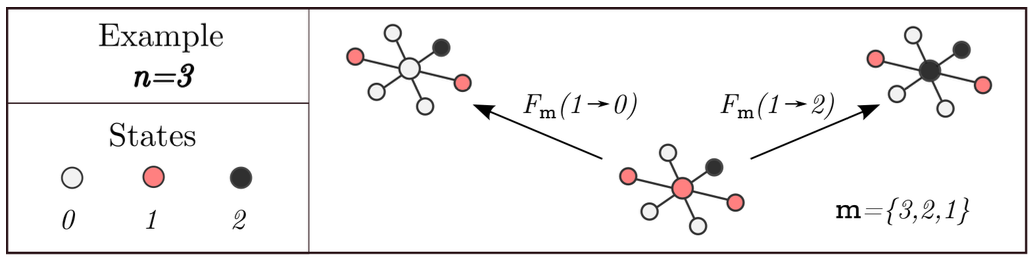
A continuous-time multistate dynamical processes is uniquely described by collection of the rate functions
, where it denotes the rate at which a node in state
changes to state
as a function of
the the number of node's neighbors in each of
states
. An object
MultistateProcess calculates transition rate matrix and
transition probability matrix given the general rates and neighbor's states .
Over the whole project we tried to use the same notation that is used in the original paper [1].
: number of different states in the dynamical process
: vector where
is number of node's neighbors in each of n states, (
)
: the rate at which a node in state
changes to state
, given the
: number of nodes in the network
: degree (
,
, min and max degrees)
: average degree in the network
: degree distribution (probability of k-degree node occurrence)
: all possible
where
An object that simulates the dynamical process, knowing the network, the transition matrix and states from the previous iteration.
A generic object for calculating multistate dynamical process which is then inherited by one of the generalized approximation framework.
Mean Field is the most relaxed, therefore, the most rough estimate of the dynamical process within the three approximation frameworks. Where we assume that the states of each node in the network are independent. In the Mean Field approximation we consider following relations:
-
expected fraction of nodes in state
of degree
at time
-
probability that the neighbor of a node is in state
at time
-
probability that a k-degree node has
-neighbor in various states at time
The Mean Field evolution equation for is:
Or having the matrix notation:
For more detailed description on Mean Field approximation see jupyter nootebook, or follow he pages 10 and 11 in the original paper [1].
TODO / not yet implemented.
TODO / not yet implemented.
The Network object is outsourced from matejker / network.
The package was developed on Python 3.6.9 and the required packages can be find in requirements
folder. To install the package from this GitHub repo using pip:
pip install git+https://github.com/matejker/MultistateProcessesOnNetworks.git@0.0.2
In order to demonstrate how it all fits together see following examples:
- Epidemic SIR model : simulation and MeanField calculation of a simple (and naive) epidemic model
Feel more than welcome to comment, commit, raise an issue, fork or push any changes. If you decide to develop be aware of
tests in tests. To check the code style and validation we use lint. Run:
make test
make lint
To install requirements run:
pip install -r ./requirements/base.txt
pip install -r ./requirements/tools.txt
pip install -r ./requirements/test.txt
[1] Peter G. Fennell, James P. Gleeson, Multistate dynamical processes on networks: Analysis through degree-based approximation frameworks, arXiv:1709.09969 [physics.soc-ph]
[2] Richard Durrett, Essentials of Stochastic Processes, Springer; 2nd ed. 2012 edition (23 May 2012)
[1] Newman, M. E. J. (2010), Networks: an introduction, Oxford University Press, Oxford; New York