dragonruby resources

Overview

I will try to collect my own notes, tips, and other fun things dragonruby related. This is also where all resources and code from the dev vlog and tutorials will go.

Index

docker: contains docker configuration for running DragonRuby

Little ruby / drgtk things

Splat operator

To have a splat oprator we need to overload the `to_a` operator:

class Vec3
  def initialize x, y, z
    @arr = [x, y, z]
  end

  def to_a
    @arr
  end
end

v = Vec3.new 2, 3, 4

p *v

Matrix Multiplication

Matrix multiplication is pretty trivial in Ruby.

def matmul mat1, mat2
  mat1.collect do |row1|
    mat2.transpose.collect do |col1|
      col1.zip(row1).inject(0) do |sum, pair|
        sum + pair[0] * pair[1]
      end
    end
  end
end

a = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
b = [[7, 8], [9, 10], [11, 12]]

matmul a, b

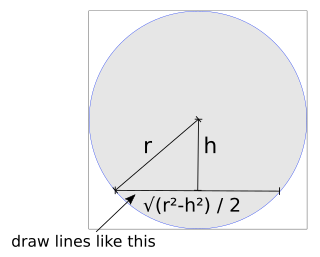
Drawing a circle using drgtk render targets

We draw images pretty simply by using pythagorean thm:

def tick args
  setup args
  display args
end

def setup args
  if args.state.tick_count == 0
    200.times do |i|
      r = 100
      h = i - r
      l = Math::sqrt(r * r - h * h)
      args.render_target(:circle).lines << [i, r - l, i, r + l]
    end

    200.times do |i|
      r1 = 100
      h1 = i - r1
      l1 = Math::sqrt(r1 * r1 - h1 * h1)
      r2 = 50
      h2 = i - r2 - r1 / 2
      if h2.abs < r2
        l2 = Math::sqrt(r2 * r2 - h2 * h2)
        args.render_target(:open_circle).lines << [i, r1 - l2, i, r1 - l1]
        args.render_target(:open_circle).lines << [i, r1 + l2, i, r1 + l1]
      else
        args.render_target(:open_circle).lines << [i, r1 - l1, i, r1 + l1]
      end
    end

    200.times do |i|
      r1 = 100
      h1 = i - r1
      l1 = Math::sqrt(r1 * r1 - h1 * h1)
      r2 = 50
      h2 = i - r2 - r1 / 3
      if h2.abs < r2
        l2 = Math::sqrt(r2 * r2 - h2 * h2)
        args.render_target(:offset_circle).lines << [i, r1 - l2, i, r1 - l1]
        args.render_target(:offset_circle).lines << [i, r1 + l2, i, r1 + l1]
      else
        args.render_target(:offset_circle).lines << [i, r1 - l1, i, r1 + l1]
      end
    end
  end
end

def display args
  args.outputs.sprites << {
    x: 500,
    y: 500,
    w: 200, h: 200, path: :circle,
    source_x: 0, source_y: 0,
    source_w: 200, source_h: 200
  }
  args.outputs.sprites << {
    x: 300,
    y: 200,
    w: 200, h: 200, path: :open_circle,
    source_x: 0, source_y: 0,
    source_w: 200, source_h: 200
  }
  args.outputs.sprites << {
    x: 800,
    y: 500,
    w: 200, h: 200, path: :offset_circle,
    source_x: 0, source_y: 0,
    source_w: 200, source_h: 200
  }
end

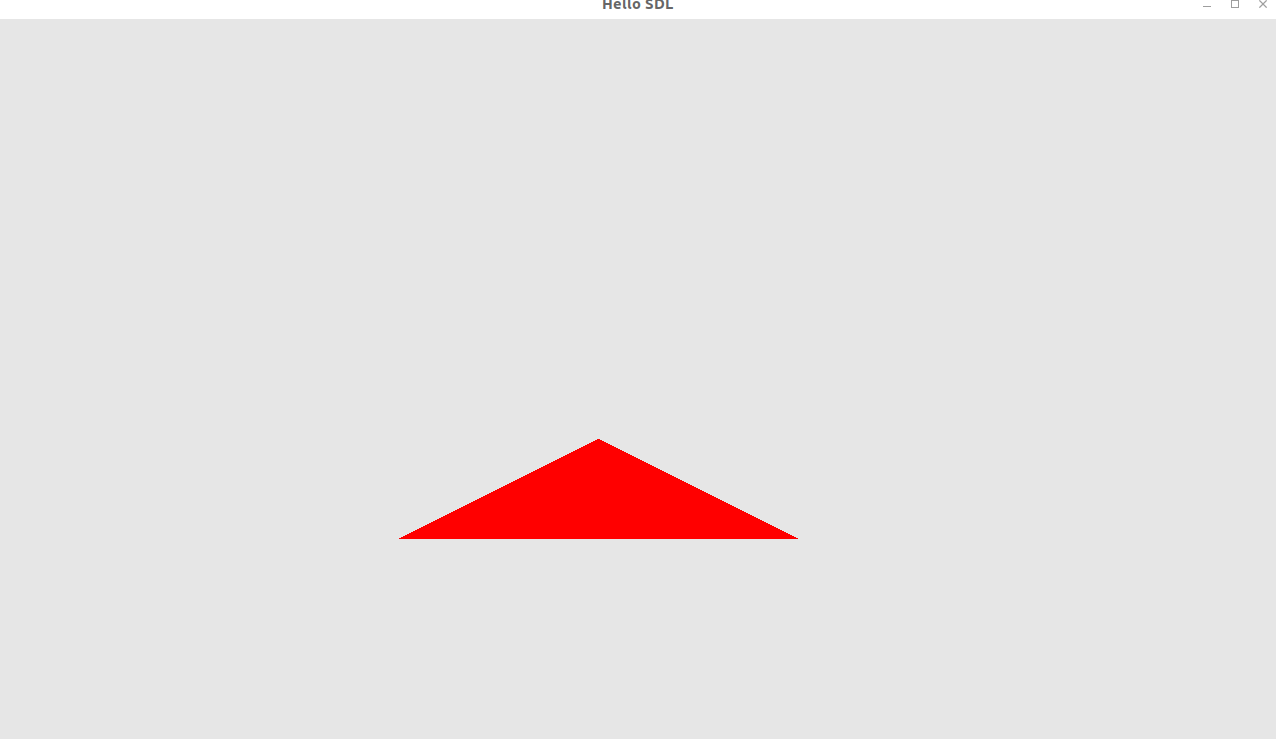
Drawing an isosceles triangle using drgtk render targets

drawing isosceles (two sides are the same length) triangles is pretty trivial:

def tick args
  if args.state.tick_count.zero?
    setup args
  end

  args.outputs.sprites << {
    x: 400, y: 200, w: args.state.triangle.w, h: args.state.triangle.h,
    r: 255, g: 0, b: 0,
    path: :triangle
  }
end

def setup args
  args.state.triangle.w = 400
  args.state.triangle.h = 100
  triangle_rt args, :triangle, args.state.triangle.w, args.state.triangle.h
end

def triangle_rt args, label, w, h
  slope = h / (w / 2)
  args.outputs[label].w = w
  args.outputs[label].h = h
  args.outputs[label].lines <<
    (args.state.triangle.w.times.map do |x|
       {
         x: x, y: 0, x2: x,
         y2: [
           slope * x,
           -slope * x + h * 2
         ].min,
         r: 255, g: 255, b: 255
       }
     end)
end

mdudzinski/dragonruby-resources