Estimate S-ARIMA-X models with Stochastic Gradient Descent or Kalman Filter
It stands for Seasonal AutoRegressive Integrated Moving Average with eXogenous variables...
The formulation is:
We need to estimate those greek letters, i.e., the S-AR, S-MA, X parameters of the model, which is said to be of order (p, d, q)(P, D, Q)[m].
First way is to use Stochastic Gradient Descent (SGD). Logic is this: we fit a large AR(p) model first, get the residuals of it and use it as the unobserved noise in the formulation. Then we form the design matrix and employ SGD to find all the parameters.
Second way is via MLE: we put the S-ARIMA-X into a (Hamiltonian) state space formulation, run a Kalman filter for likelihood and a numerical optimizer solves for parameters (e.g, L-BFGS). statsmodels does something like this, too; but they also offer Harvey's representation (that's the default and used in below example).
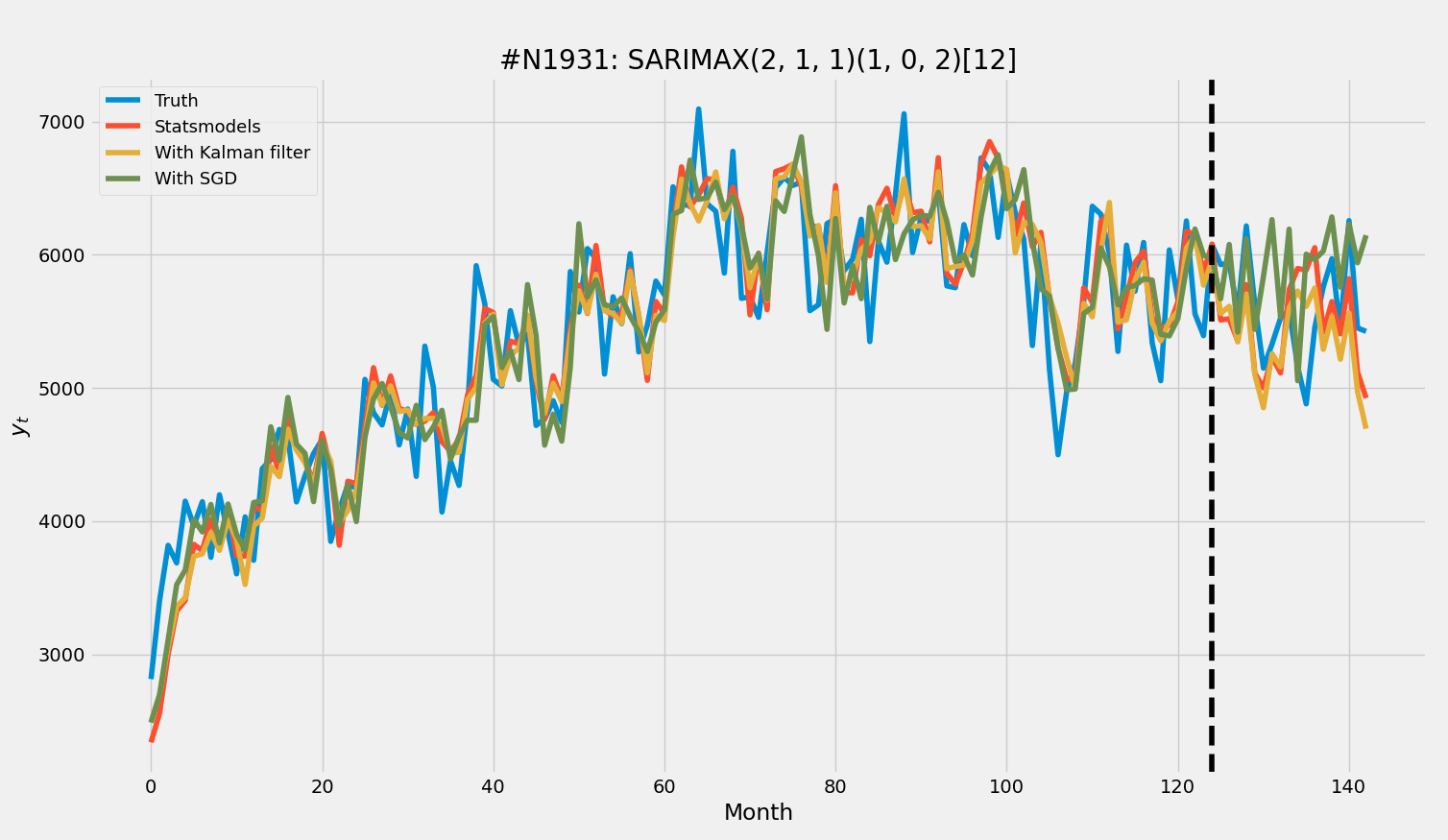
Here is a sample monthly data from M3 Competiton dataset. Black vertical line is train-test split point. All models have the order (2, 1, 1)(1, 0, 2)[12]:
For SGD:
from sgd_sarimax import SARIMAX_SGD
model = SARIMAX_SGD(endog, exog, order=(2, 1, 3), seas_order=(1, 1, 0, 4))
model.fit(max_iter=5_000, eta0=0.1)
preds_in_sample = model.predict_in_sample()
forecasts = model.forecast(steps=10)For KF:
from kalman_sarimax import SARIMAX_KF
model = SARIMAX_KF(endog, exog, order=(2, 1, 3), seas_order=(1, 1, 0, 4))
model.fit()
preds_in_sample = model.predict_in_sample()
forecasts = model.forecast(steps=10)