Importance Weighted Autoencoders in TensorFlow 2

Reproducing results from the IWAE paper in TensorFlow 2.

Results

Samples (left) and mean function (right) when sampling from the prior, during training of an IWAE with 50 importance samples.

Test-set log likelihoods as estimated using k=5000 importance samples:

1 stochastic layer

Method	Test-set LLH	Test-set LLH (original paper)
IWAE k=1	-86.35	-86.76
IWAE k=5	-85.18	-85.54
IWAE k=50	-84.59	-84.78

2 stochastic layers

Method	Test-set LLH (this repo)	Test-set LLH (original paper)
IWAE k=1	-84.83	-85.33
IWAE k=5	-83.48	-83.89
IWAE k=50	-82.82	-82.90

Usage

The results for the IWAE with 1 or 2 stochastic layers and 1, 5 or 50 importance samples can be obtained by running main.py as

python main.py --n_samples          <# of importance samples, 5 by default>  
               --objective          <choose iwae_elbo or vae_elbo, iwae_elbo by default>
               --stochastic_layers  <# of stochastic layers, 1 by default>

The model is investigated further in a series of tasks found in ./tasks.
task01.py: Use a 2D latent space to investigate both true and variational posteriors. We can use self-normalized importance sampling to estimate posterior means and sampling importance resampling to draw samples from the true posterior.
task02.py: Apply the Doubly Reparameterized Gradient Estimator, DReG, to the original experiment.
task03.py: Investigates the latent spaces of an IWAE with two stochastic layers. task04.py: Extend the experiment in main.py to a conditional IWAE, conditioned on the image labels.

Additional results:

DReG estimator, 1 stochastic layer

The Doubly Reparameterized Gradient Estimator for Monte Carlo Objectives, DReG, provides even lower variance gradients for the inference network, than just using the reparameterization trick. This is implemented in task02.py.

Method	DReG Test-set LLH	Standard IWAE Test-set LLH
IWAE k=1	-86.08	-86.35
IWAE k=5	-84.90	-85.18
IWAE k=50	-84.32	-84.59

Variational and true posteriors

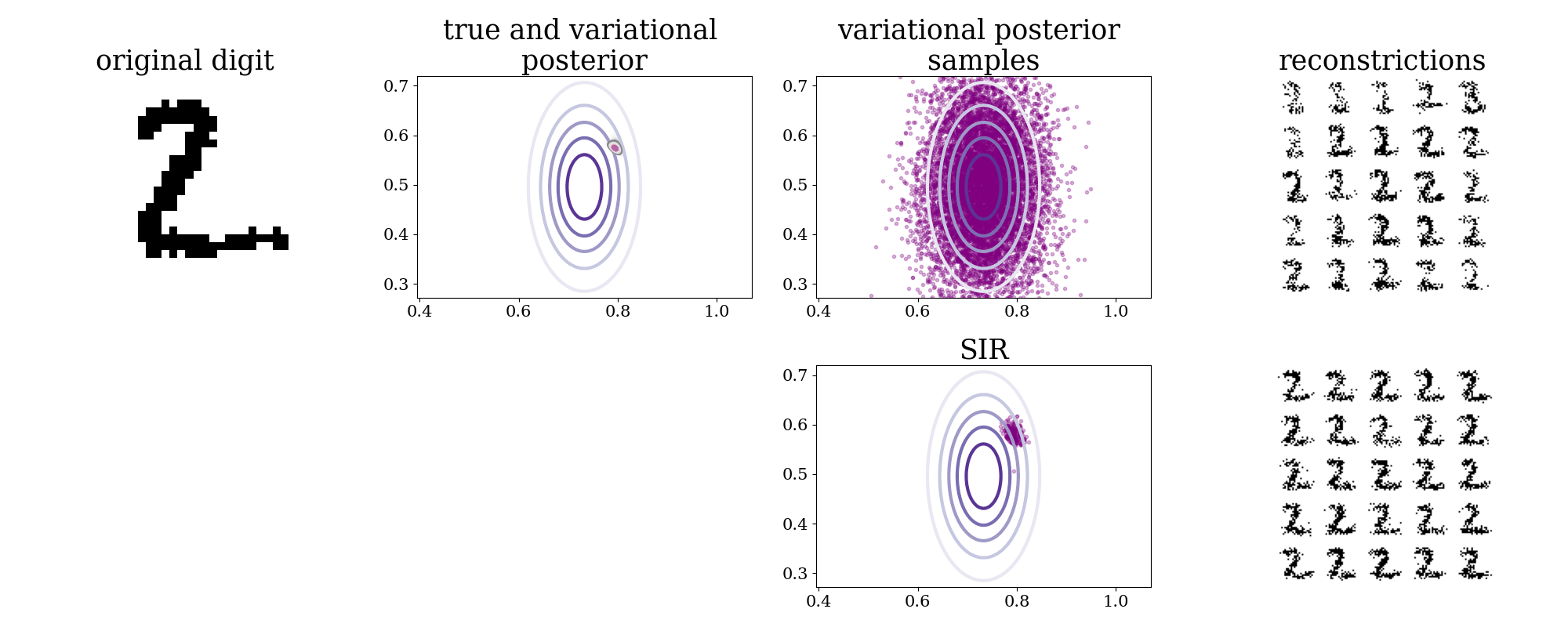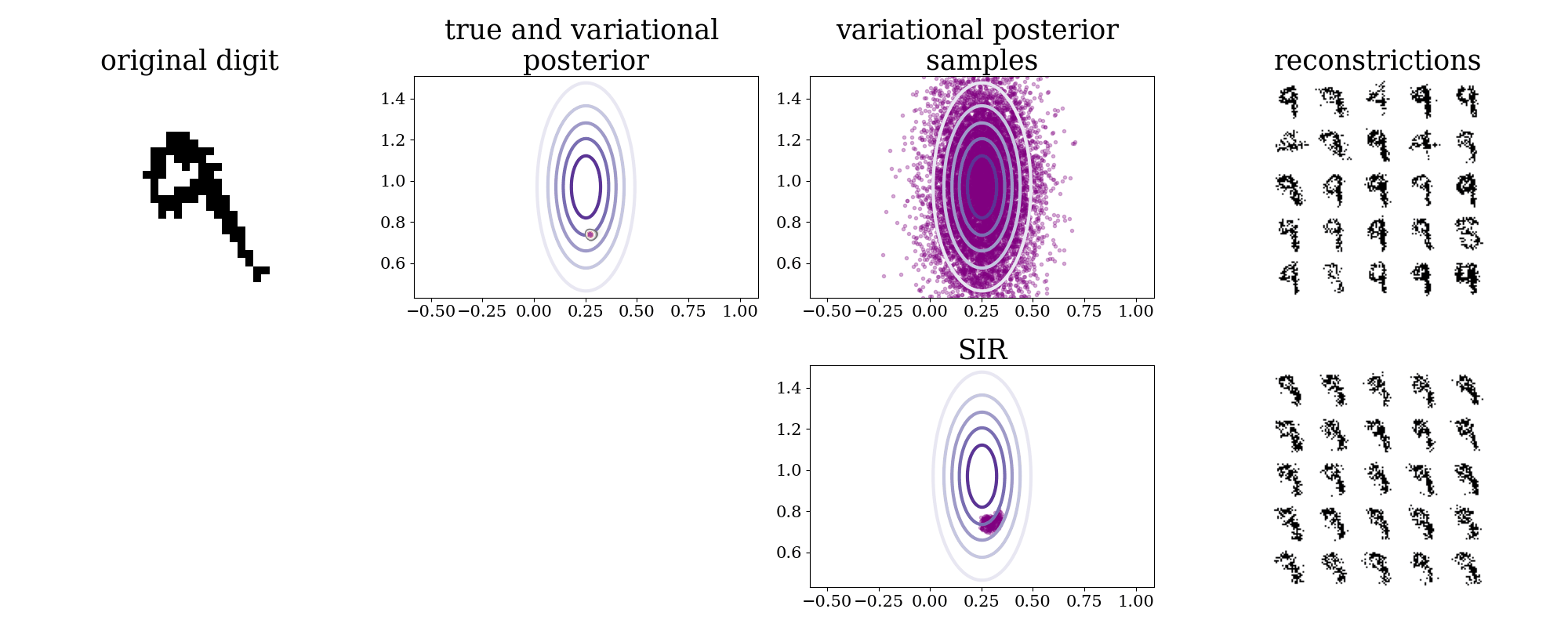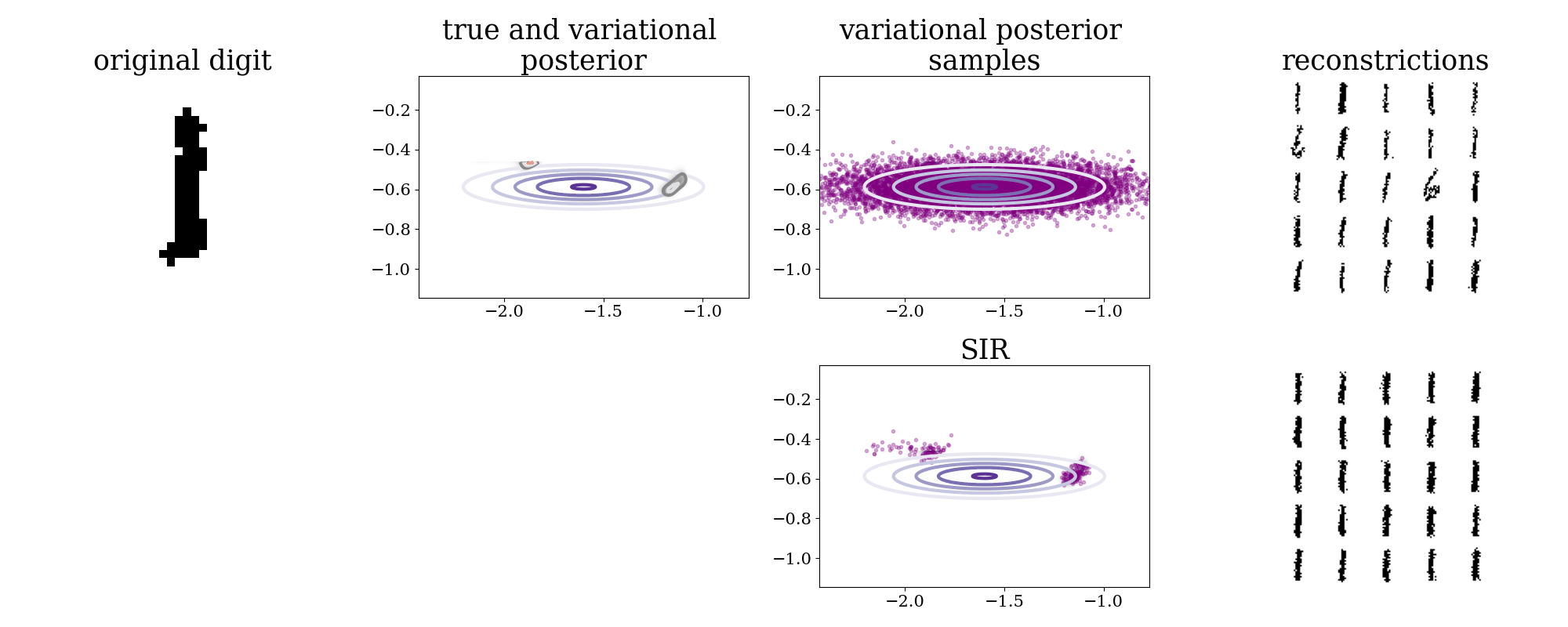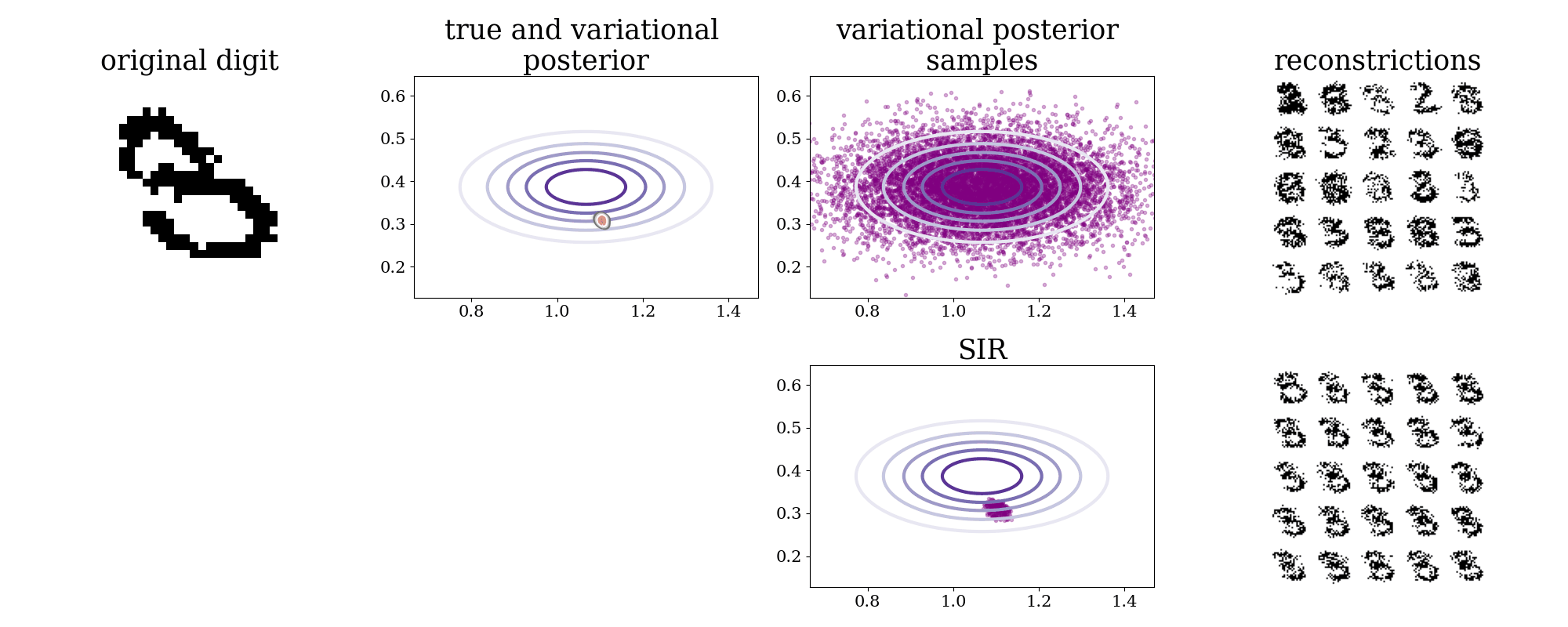
In an IWAE with a 2D latent space we can inspect the true posterior, by evaluating it over a grid. This is done in task01.py.
In the two left most plots below are shown a digit from the test-set alongside its true and variational posteriors. The variational posterior is axis aligned and usually covers the more complex true posterior. To the right are shown samples from the variational posterior and reconstructions of some of these. The bottom row shows how sampling importance resampling, using the self-normalized importance weights, can provide samples from the true posterior.

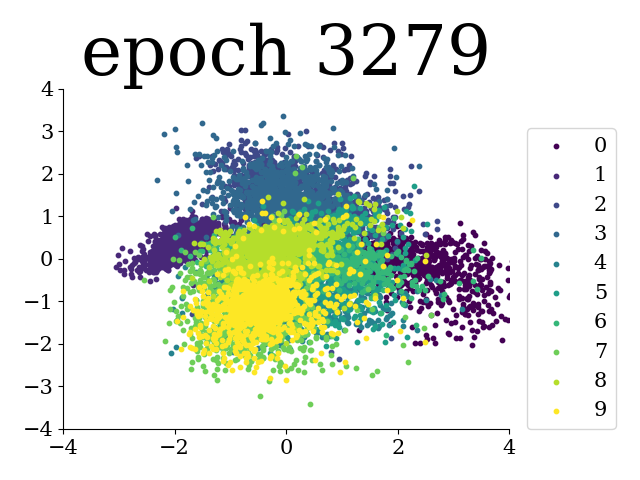
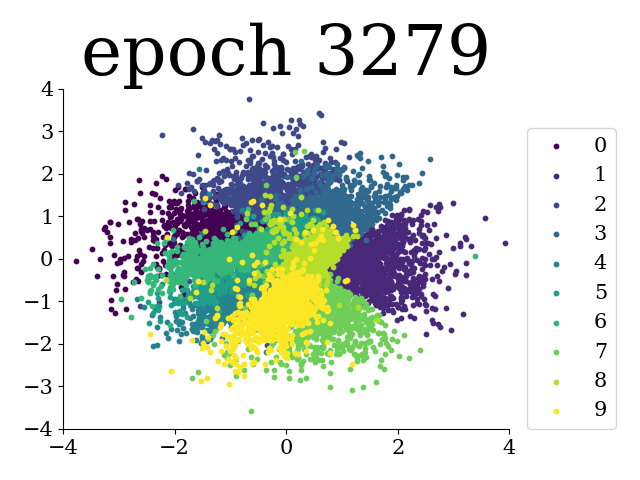
Latent representations with 2 stochastic layers

In task03.py we fit an IWAE with 2 stochastic layers of dimension 4 and 2 respectively. The (PCA of) the latent representations are seen below. The expectation of the latent representations are obtained using self-normalized importance sampling. The first layer to the left and the second layer to the right.

Regular VAE results

By running main.py with --objective vae_elbo the VAE results from the IWAE paper can be reproduced.

1 stochastic layer VAE

Method	Test-set LLH (this repo)	Test-set LLH (original paper)
VAE k=1	-86.35	-86.76
VAE k=5	-86.10	-86.47
VAE k=50	-86.06	-86.35

2 stochastic layers VAE

Method	Test-set LLH (this repo)	Test-set LLH (original paper)
VAE k=1	-84.83	-85.33
VAE k=5	-84.08	-85.01
VAE k=50	-83.89	-84.78

CVAE 1 stochastic layer

The Conditional VAE (IWAE in this case) can be coditioned on some context, in this case the image labels. The prior can be the usual prior (task05.py) or conditional on the label as well (task04.py). In these results the prior is conditional on the label.

Method	Test-set LLH
CIWAE k=1	-82.32
CIWAE k=5	-81.41
CIWAE k=50	-80.78

TODO:

Investigate active units

Resources:

Two stochastic layers

xqding
ShwanMario
addtt
Ladder VAE and accompanying github

nbip/IWAE