I am currently involved in the estimation of the population size of the brown bear population in the Pyrenees. So far, we have been using a frequentist capture-recapture approach using the robust design. Because it is a small population, I'm interested in implementing a Bayesian approach. To do so, Thomas Riecke and colleagues have proposed a parameterization and some BUGS code to fit robust-design capture-recapture methods. Here, I am using the code they made available, tweaking it a bit and making it generic. Also, I provide a fully reproducible example. For more details about the robust design, check out the dedicated chapter in the Gentle Introduction to Mark. For extension of the Riecke's model to Jolly-Seber models, see here, and for an alternative Bayesian implementation of the robust design, check out the work by Robert Rankin and colleagues there.
I will use a robust design example data set that comes with program MARK, check out ?RMark::robust.
First, we load the packages we will need in this section:
library(RMark)
library(tidyverse)Then we load the data
data(robust)
head(robust)## ch freq
## 1 000000111011101 1
## 2 000000111111000 1
## 3 000001000000000 2
## 4 000001001110100 1
## 5 000001010000000 1
## 6 000001100000010 1
We need to define the time intervals:
time.intervals <- c(0, 1, # primary occasion 1, 2 secondary occasions
0, 1, # primary occasion 2, 2 secondary occasions
0, 0, 0, 1, # primary occasion 3, 4 secondary occasions
0, 0, 0, 0, 1, # primary occasion 4, 5 secondary occasions
0) # primary occasion 5, 2 secondary occasionsWe fit a model with constant survival, constant detection and random temporary emigration:
p.dot <- list(formula=~1, share = TRUE)
S.dot <- list(formula=~1)
GammaDoublePrime.dot <- list(formula=~1,
share = TRUE)
model.1 <- mark(data = robust,
model = "Robust",
time.intervals = time.intervals,
model.parameters = list(S = S.dot,
GammaDoublePrime = GammaDoublePrime.dot,
p = p.dot),
threads=2,
output = FALSE)Print the parameter estimates:
model.1$results$real## estimate se lcl ucl fixed
## S g1 c1 a0 t1 0.8312500 0.0079641 0.8150602 0.8462897
## Gamma'' g1 c1 a0 t1 0.1336015 0.0109793 0.1135085 0.1566228
## p g1 s1 t1 0.6064105 0.0059031 0.5947827 0.6179190
## f0 g1 a0 s1 t0 163.3785700 15.0915830 136.3746200 195.7296700
## f0 g1 a0 s2 t0 125.0667300 12.9788300 102.1040500 153.1936000
## f0 g1 a0 s3 t0 15.9713820 4.2317023 9.5856695 26.6110840
## f0 g1 a0 s4 t0 4.2875764 2.2322650 1.6418392 11.1967790
## f0 g1 a0 s5 t0 52.8422130 8.1674652 39.1011790 71.4121550
## note
## S g1 c1 a0 t1
## Gamma'' g1 c1 a0 t1
## p g1 s1 t1
## f0 g1 a0 s1 t0
## f0 g1 a0 s2 t0
## f0 g1 a0 s3 t0
## f0 g1 a0 s4 t0
## f0 g1 a0 s5 t0
and the population size estimates:
model.1$results$derived$`N Population Size`## estimate lcl ucl
## 1 1057.3786 1030.3746 1089.7297
## 2 810.0667 787.1041 838.1936
## 3 685.9714 679.5857 696.6111
## 4 507.2876 504.6418 514.1968
## 5 343.8422 330.1012 362.4122
We fit the same model with Markovian temporary emigration now:
p.dot <- list(formula=~1, share = TRUE)
S.dot <- list(formula=~1)
GammaDoublePrime.dot <- list(formula=~1)
GammaPrime.dot <- list(formula=~1)
model.2 <- mark(data = robust,
model = "Robust",
time.intervals = time.intervals,
model.parameters = list(S = S.dot,
GammaPrime = GammaPrime.dot,
GammaDoublePrime = GammaDoublePrime.dot,
p = p.dot),
threads=2,
output = FALSE)Print the parameter estimates:
model.2$results$real## estimate se lcl ucl fixed
## S g1 c1 a0 t1 0.8308413 0.0082652 0.8140186 0.8464294
## Gamma'' g1 c1 a0 t1 0.1335610 0.0109476 0.1135226 0.1565119
## Gamma' g1 c1 a1 t2 0.1246823 0.0513209 0.0536314 0.2636393
## p g1 s1 t1 0.6064240 0.0059038 0.5947949 0.6179338
## f0 g1 a0 s1 t0 163.3651400 15.0911060 136.3621600 195.7153600
## f0 g1 a0 s2 t0 125.0566200 12.9783840 102.0948400 153.1826500
## f0 g1 a0 s3 t0 15.9690640 4.2314181 9.5839088 26.6082450
## f0 g1 a0 s4 t0 4.2867419 2.2320757 1.6413658 11.1956500
## f0 g1 a0 s5 t0 52.8378900 8.1671244 39.0975140 71.4071650
## note
## S g1 c1 a0 t1
## Gamma'' g1 c1 a0 t1
## Gamma' g1 c1 a1 t2
## p g1 s1 t1
## f0 g1 a0 s1 t0
## f0 g1 a0 s2 t0
## f0 g1 a0 s3 t0
## f0 g1 a0 s4 t0
## f0 g1 a0 s5 t0
and the population size estimates:
model.2$results$derived$`N Population Size`## estimate lcl ucl
## 1 1057.3651 1030.3622 1089.7154
## 2 810.0566 787.0948 838.1827
## 3 685.9691 679.5839 696.6082
## 4 507.2867 504.6414 514.1956
## 5 343.8379 330.0975 362.4072
Now that we have our results with the frequentist approach, let's implement the Bayesian approach and compare the estimates.
First, we separate the columns of the capture-recapture dataset:
chx <- NULL
for (i in 1:nrow(robust)){
chx <- rbind(chx, unlist(str_split(robust$ch[i],'')))
}
head(chx)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
## [1,] "0" "0" "0" "0" "0" "0" "1" "1" "1" "0" "1" "1" "1" "0"
## [2,] "0" "0" "0" "0" "0" "0" "1" "1" "1" "1" "1" "1" "0" "0"
## [3,] "0" "0" "0" "0" "0" "1" "0" "0" "0" "0" "0" "0" "0" "0"
## [4,] "0" "0" "0" "0" "0" "1" "0" "0" "1" "1" "1" "0" "1" "0"
## [5,] "0" "0" "0" "0" "0" "1" "0" "1" "0" "0" "0" "0" "0" "0"
## [6,] "0" "0" "0" "0" "0" "1" "1" "0" "0" "0" "0" "0" "0" "1"
## [,15]
## [1,] "1"
## [2,] "0"
## [3,] "0"
## [4,] "0"
## [5,] "0"
## [6,] "0"
Now we need to duplicate the encounter histories for which there more than one individual with that partcular history:
encounter <- NULL
for (i in 1:length(robust$freq)){
if (robust$freq[i] == 1) encounter <- rbind(encounter, as.numeric(chx[i,]))
if (robust$freq[i] > 1) encounter <- rbind(encounter, matrix(rep(as.numeric(chx[i,]), robust$freq[i]), nrow = robust$freq[i], byrow= T))
}
head(encounter)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
## [1,] 0 0 0 0 0 0 1 1 1 0 1 1 1 0
## [2,] 0 0 0 0 0 0 1 1 1 1 1 1 0 0
## [3,] 0 0 0 0 0 1 0 0 0 0 0 0 0 0
## [4,] 0 0 0 0 0 1 0 0 0 0 0 0 0 0
## [5,] 0 0 0 0 0 1 0 0 1 1 1 0 1 0
## [6,] 0 0 0 0 0 1 0 1 0 0 0 0 0 0
## [,15]
## [1,] 1
## [2,] 0
## [3,] 0
## [4,] 0
## [5,] 0
## [6,] 0
We compute several quantities that we will need:
n.ind <- nrow(encounter) # number of individuals
n.secondary <- c(2, 2, 4, 5, 2) # number of secondary occasions per primary occasion
n.primary <- length(n.secondary) # number of primary occasions
index <- list(1:2,
3:4,
5:8,
9:13,
14:15) # the secondary occasionsWe calculate the number of individuals caught in each primary occasion, which we will need to get an estimate of population size:
caught <- rep(NA, n.primary)
for (i in 1:n.primary){
tmp <- encounter[,index[[i]]]
caught[i] <- nrow(tmp[rowSums(tmp)!=0,])
}
caught## [1] 894 685 670 503 291
We format the data as an array with dimensions the number of individuals times the number of primary occasions times the number of secondary occasions:
obs <- array(NA, dim = c(n.ind, n.primary, max(n.secondary)))
for (i in 1:n.primary){
obs[,i,1:n.secondary[i]] <- encounter[,index[[i]]]
}
dim(obs)## [1] 991 5 5
Now we format the data as required in the Bayesian implementation of the robust design:
ch <- matrix(NA, n.ind, n.primary)
for (i in 1:n.ind){
for (t in 1:n.primary){
ifelse(any(obs[i,t,1:n.secondary[t]] == 1), ch[i,t] <- 1, ch[i,t] <- 2)
}
}We summarize detections by primary and secondary occasions:
test <- matrix(NA, n.ind, n.primary)
for (i in 1:nrow(test)){
for (j in 1:ncol(test)){
test[i,j] <- sum(obs[i,j,], na.rm = TRUE)
}
}
seen <- array(NA, c(n.ind, n.primary, max(n.secondary)))
missed <- array(NA, c(n.ind, n.primary, max(n.secondary)))
for (i in 1:nrow(test)){
for (t in 1:ncol(test)){
for (j in 1:n.secondary[t]){
if(test[i,t] > 1 & obs[i,t,j] == 1){seen[i,t,j] <- 1}
if(test[i,t] >= 1 & obs[i,t,j] == 0){missed[i,t,j] <- 1}
}
}
}
yes <- matrix(NA, n.primary, max(n.secondary))
no <- matrix(NA, n.primary, max(n.secondary))
for (i in 1:nrow(yes)){
for (j in 1:ncol(yes)){
yes[i,j] <- sum(seen[,i,j], na.rm = TRUE)
no[i,j] <- sum(missed[,i,j], na.rm = TRUE)
}
}
total <- yes + no
total## [,1] [,2] [,3] [,4] [,5]
## [1,] 649 690 0 0 0
## [2,] 466 509 0 0 0
## [3,] 652 628 644 652 0
## [4,] 497 501 491 494 499
## [5,] 187 195 0 0 0
Get first occasions of capture:
get.first <- function(x)min(which (x != 2))
first <- apply(ch,1,get.first); first[first == "Inf"] <- NACut individuals released in last primary occasion:
ch <- subset(ch, first != n.primary)
first <- subset(first, first != n.primary)Define initial values for the latent states:
z.init <- matrix(NA, nrow(ch), ncol(ch))
for (i in 1:nrow(ch)){
if(first[i] < ncol(z.init)){
z.init[i,(first[i] + 1):ncol(z.init)] <- 1
}
}Load the package we need to carry out Bayesian analyses:
library(R2jags)The code:
model <- function() {
# priors
phi ~ dunif(0,1) # survival
gP ~ dunif(0,1) # gamma'
gPP ~ dunif(0,1) # gamma''
gamP <- 1 - gP # MARK parameterization
gamPP <- 1 - gPP # MARK parameterization
mean.p ~ dunif(0,1) # detection
# secondary occasions p's
for (t in 1:n.years){
for (j in 1:max(n.sec[1:n.years])){
p[t,j] <- mean.p
}
}
for (t in 1:n.years){
for (j in 1:n.sec[t]){
yes[t,j] ~ dbin(p[t,j], total[t,j])
}
}
# Primary occasions p's or pooled detection probability
for (t in 1:n.years){
pstar[t] <- 1 - prod(1 - p[t,1:n.sec[t]])
}
# state matrices
s[1,1] <- phi * gPP
s[1,2] <- phi * (1 - gPP)
s[1,3] <- 1 - phi
s[2,1] <- phi * gP
s[2,2] <- phi * (1 - gP)
s[2,3] <- 1 - phi
s[3,1] <- 0
s[3,2] <- 0
s[3,3] <- 1
# observation matrices
for (t in 1:n.years){
o[1,t,1] <- pstar[t]
o[1,t,2] <- 1 - pstar[t]
o[2,t,1] <- 0
o[2,t,2] <- 1
o[3,t,1] <- 0
o[3,t,2] <- 1
}
# likelihood
for (i in 1:n.ind){
z[i,first[i]] <- ch[i,first[i]]
for (t in (first[i]+1):n.years){
z[i,t] ~ dcat(s[z[i,t-1], ]) # state equations
ch[i,t] ~ dcat(o[z[i,t], t, ]) # obsevation equations
}
}
}Build the list of data
dat <- list(first = first,
ch = ch,
n.sec = n.secondary,
n.years = ncol(ch),
n.ind = nrow(ch),
yes = yes,
total = total)The initial values:
inits <- function(){list(z = z.init)}Define the parameters we'd like to monitor:
pars <- c('pstar','mean.p','phi','gamP','gamPP')The MCMC settings (number of iterations for burnin and post-inference probably need to be increased):
n.chains <- 1
n.iter <- 1000
n.burnin <- 500And run the model:
res_markovian <- jags(data = dat,
inits = inits,
parameters.to.save = pars,
model.file = model,
n.chains = n.chains,
n.iter = n.iter,
n.burnin = n.burnin)## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 3865
## Unobserved stochastic nodes: 3854
## Total graph size: 16615
##
## Initializing model
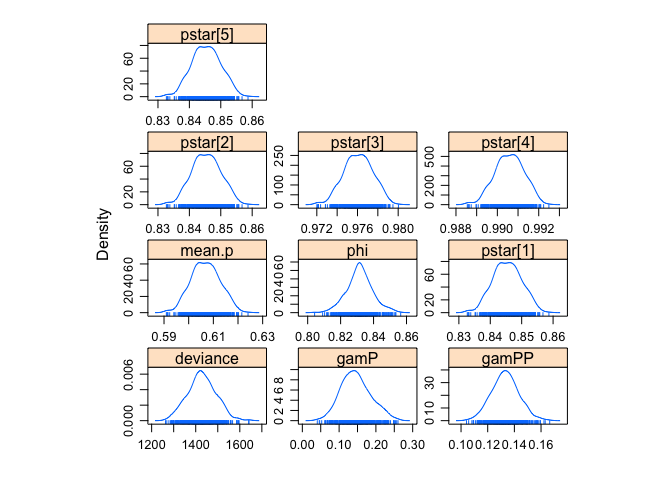
Posterior density distribution of the parameters:
library(lattice)
jagsfit.mcmc <- as.mcmc(res_markovian)
densityplot(jagsfit.mcmc)Display the results:
summary(jagsfit.mcmc)##
## Iterations = 501:1000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 500
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## deviance 1428.3359 6.463e+01 2.890e+00 5.188e+00
## gamP 0.1461 4.070e-02 1.820e-03 4.874e-03
## gamPP 0.1332 1.028e-02 4.598e-04 1.238e-03
## mean.p 0.6069 5.824e-03 2.604e-04 3.696e-04
## phi 0.8316 7.961e-03 3.560e-04 6.074e-04
## pstar[1] 0.8454 4.579e-03 2.048e-04 2.908e-04
## pstar[2] 0.8454 4.579e-03 2.048e-04 2.908e-04
## pstar[3] 0.9761 1.416e-03 6.334e-05 9.010e-05
## pstar[4] 0.9906 6.965e-04 3.115e-05 4.434e-05
## pstar[5] 0.8454 4.579e-03 2.048e-04 2.908e-04
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## deviance 1304.4318 1387.9691 1426.5497 1468.3835 1549.2666
## gamP 0.0738 0.1171 0.1432 0.1724 0.2303
## gamPP 0.1136 0.1264 0.1332 0.1398 0.1538
## mean.p 0.5963 0.6029 0.6067 0.6109 0.6179
## phi 0.8156 0.8268 0.8315 0.8362 0.8488
## pstar[1] 0.8370 0.8423 0.8453 0.8486 0.8540
## pstar[2] 0.8370 0.8423 0.8453 0.8486 0.8540
## pstar[3] 0.9734 0.9751 0.9761 0.9771 0.9787
## pstar[4] 0.9893 0.9901 0.9906 0.9911 0.9919
## pstar[5] 0.8370 0.8423 0.8453 0.8486 0.8540
Provide posterior means for population size:
Nmcmc <- matrix(NA, nrow(res_markovian$BUGSoutput$sims.list$pstar), n.primary)
for (i in 1:n.primary){
Nmcmc[,i] <- caught[i] / res_markovian$BUGSoutput$sims.list$pstar[,i]
}
apply(Nmcmc,2,mean)## [1] 1057.5016 810.2781 686.4191 507.7790 344.2203
If we compare to the frequentist results, we're pretty close I'd say. Now let's fit the model with random emigration.
The code:
model <- function() {
# priors
phi ~ dunif(0,1) # survival
gamma ~ dunif(0,1) # gamma
gam <- 1 - gamma # MARK parameterization
mean.p ~ dunif(0,1) # detection
# secondary occasions p's
for (t in 1:n.years){
for (j in 1:max(n.sec[1:n.years])){
p[t,j] <- mean.p
}
}
for (t in 1:n.years){
for (j in 1:n.sec[t]){
yes[t,j] ~ dbin(p[t,j], total[t,j])
}
}
# primary occasions p's or pooled detection probability
for (t in 1:n.years){
pstar[t] <- 1 - prod(1 - p[t,1:n.sec[t]])
}
# likelihood
for (i in 1:n.ind){
z[i,first[i]] <- ch[i,first[i]]
for (t in (first[i]+1):n.years){
mu1[i,t] <- z[i,t-1] * phi
mu2[i,t] <- z[i,t] * (gamma) * pstar[t]
z[i,t] ~ dbern(mu1[i,t]) # state equations
ch[i,t] ~ dbern(mu2[i,t]) # observation equations
}
}
}The data
ch[ch == 2] <- 0 # Bernoulli likelihood
dat <- list(first = first,
ch = ch,
n.sec = n.secondary,
n.years = ncol(ch),
n.ind = nrow(ch),
yes = yes,
total = total)Then initial values, parameters to monitor, MCMC settings (number of iterations for burnin and post-inference probably need to be increased)
inits <- function(){list(z = z.init)}
pars <- c('pstar','mean.p','phi','gam')
n.chains <- 1
n.iter <- 1000
n.burnin <- 500We are ready to fit the model to the data:
res_random <- jags(data = dat,
inits = inits,
parameters.to.save = pars,
model.file = model,
n.chains = n.chains,
n.iter = n.iter,
n.burnin = n.burnin)## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 3865
## Unobserved stochastic nodes: 3853
## Total graph size: 16589
##
## Initializing model
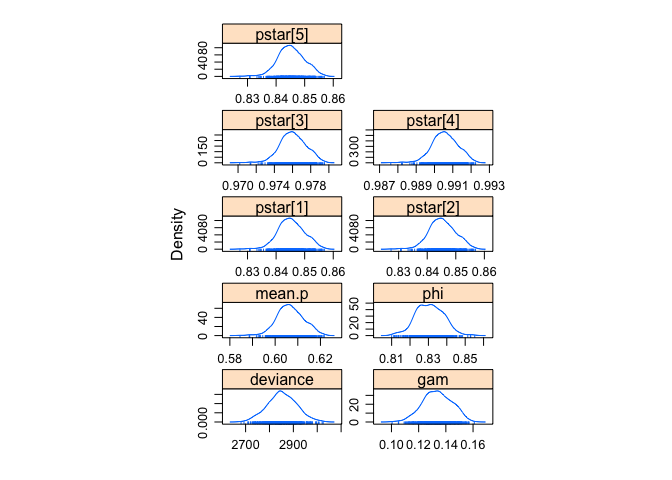
Posterior density distribution of the parameters:
jagsfit.mcmc <- as.mcmc(res_random)
densityplot(jagsfit.mcmc)Display the results:
summary(jagsfit.mcmc)##
## Iterations = 501:1000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 500
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## deviance 2852.9690 6.053e+01 2.707e+00 5.769e+00
## gam 0.1337 1.058e-02 4.732e-04 8.440e-04
## mean.p 0.6067 5.880e-03 2.629e-04 3.259e-04
## phi 0.8308 7.525e-03 3.365e-04 4.952e-04
## pstar[1] 0.8453 4.627e-03 2.069e-04 2.566e-04
## pstar[2] 0.8453 4.627e-03 2.069e-04 2.566e-04
## pstar[3] 0.9760 1.435e-03 6.416e-05 7.958e-05
## pstar[4] 0.9906 7.065e-04 3.160e-05 3.920e-05
## pstar[5] 0.8453 4.627e-03 2.069e-04 2.566e-04
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## deviance 2736.3198 2811.8658 2849.3106 2894.0071 2972.9760
## gam 0.1130 0.1265 0.1337 0.1415 0.1528
## mean.p 0.5961 0.6027 0.6065 0.6105 0.6176
## phi 0.8160 0.8253 0.8307 0.8362 0.8451
## pstar[1] 0.8369 0.8422 0.8451 0.8483 0.8538
## pstar[2] 0.8369 0.8422 0.8451 0.8483 0.8538
## pstar[3] 0.9734 0.9751 0.9760 0.9770 0.9786
## pstar[4] 0.9892 0.9901 0.9906 0.9910 0.9918
## pstar[5] 0.8369 0.8422 0.8451 0.8483 0.8538
Provide posterior means for population size:
Nmcmc <- matrix(NA, nrow(res_random$BUGSoutput$sims.list$pstar), n.primary)
for (i in 1:n.primary){
Nmcmc[,i] <- caught[i] / res_random$BUGSoutput$sims.list$pstar[,i]
}
apply(Nmcmc,2,mean)## [1] 1057.6403 810.3843 686.4435 507.7878 344.2655
Again, pretty close.