Task

The task is to find unknown mathematical formula y=f(x), which is hidden in a black-box machine. You can measure data by the following request:

<IP>/api/do_measurement?x=4

You get a response in JSON like this:

{"data": {"y": 188.58938971580736, "x": 4.0}}

The full text of the task is here https://github.com/kiwicom/mlweekend

Solution

The solution is written in Python 3 (tested on 3.5.4).

Get data

get_data.py can be used to do a series of measurements on a given interval, with a given step and a number of repetitions, e.g.

python get_data.py -1 1.1 0.1 5

performs measurements on the interval <-1.0,1.0>, with step 0.1, and with 5 repetitions for every x value. The data are saved into txt file, where the first column contains x data and the other ones y data.

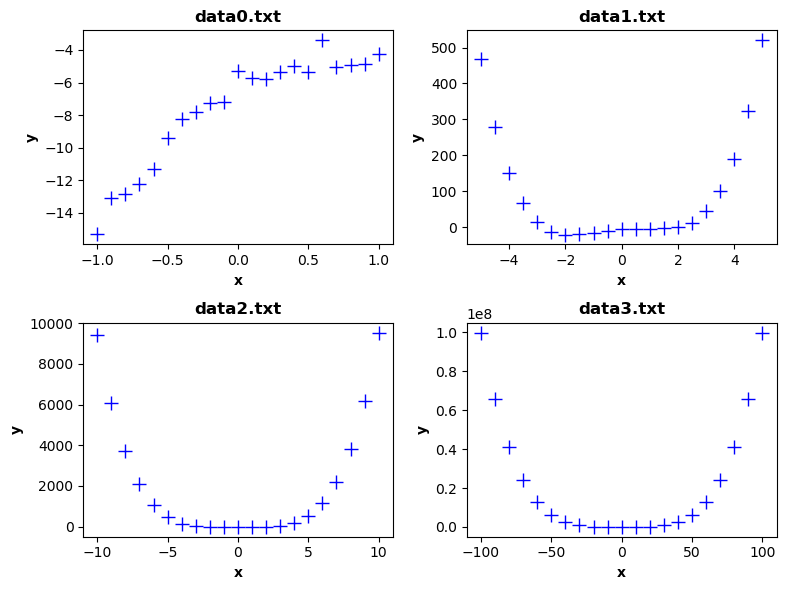
There are 4 testing datasets obtained by the script in this repository:

data0.txt - interval <-1.0,1.0>, step 0.1, rep 5
data1.txt - interval <-5.0,5.0>, step 0.5, rep 5
data2.txt - interval <-10,10>, step 1, rep 5
data3.txt - interval <-100,100>, step 10, rep 5

First look

The function for x close to zero (<-1.0,1.0>) is quite weird, but for higher x values, it looks like a power function. According to the y values (e.g. 10000~f(10)), it could be y=x^4. For better approximation, 4th order polynomial function could work fine.

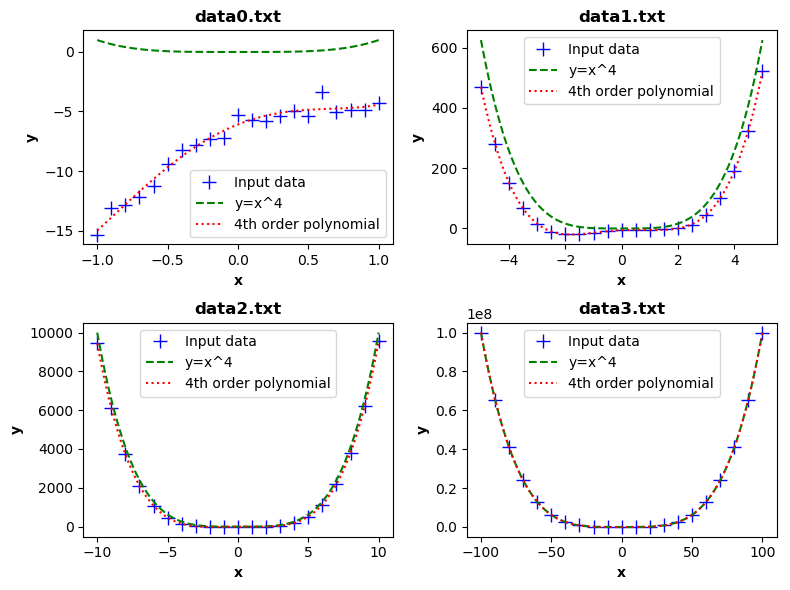
Approximations

find_formula.py app is for finding and testing approximations. At first, it checks data and interpolates missing values. If there are more measurements for one x, the y values are averaged, which produces a basic filtration. These input data are approximated using y=x^4 power function and 4th order polynomial function (least squares fit) - the assumption of the data scientist :) The app works as follows:

python find_formula.py data0.txt

This processes the given dataset and produces plots comparing above mentioned approximation functions. Here is the graphical summary of all the datasets:

Conclusion

There is no only clear solution. For small intervals close to zero, polynomial approximation works well; on the other hand, the power function can't be used in this case. For example, this is a suitable approximation for dataset data1.txt:

y = 1.002 x^4 + 0.007143 x^3 - 5.037 x^2 + 4.8 x - 5.608