pineapple-bois/Double_Pendulum

Lagrangian derivation of double pendulum equations of motion

Double Pendulum Equations of Motion

Lagrangian Formulation

---

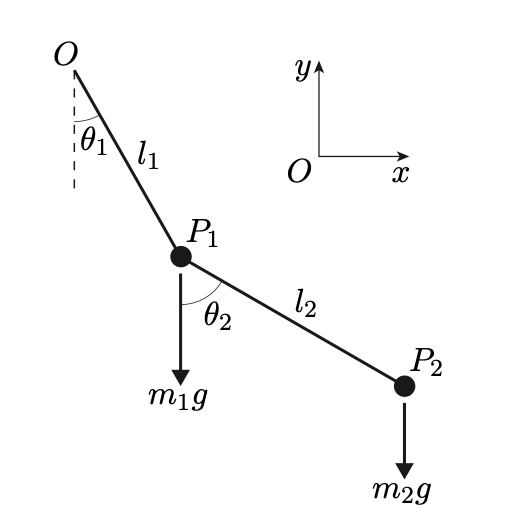
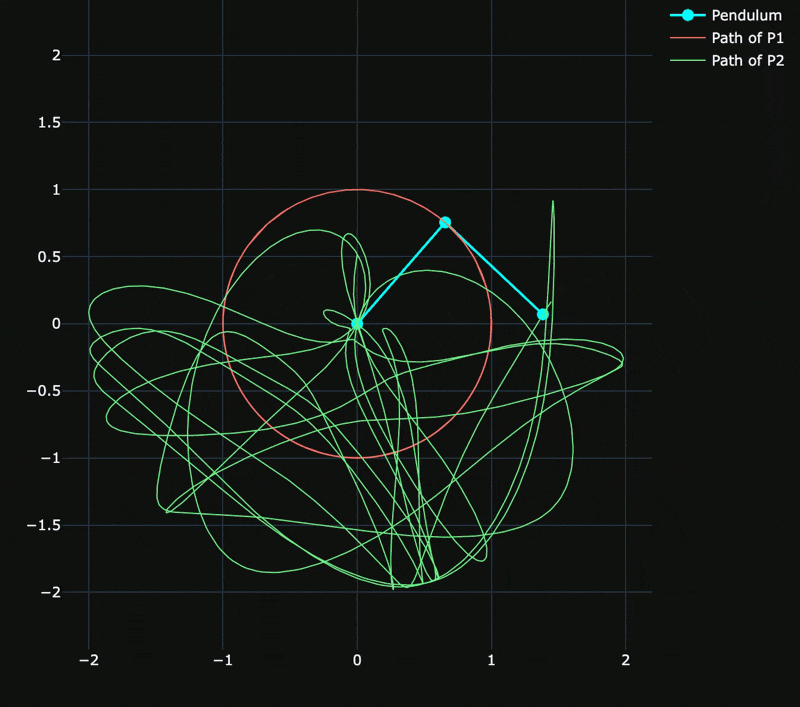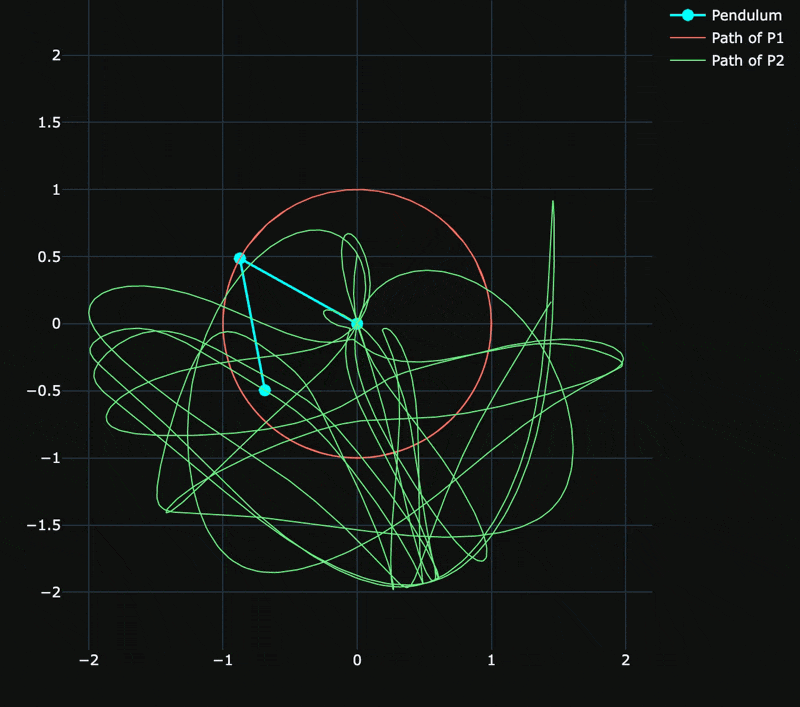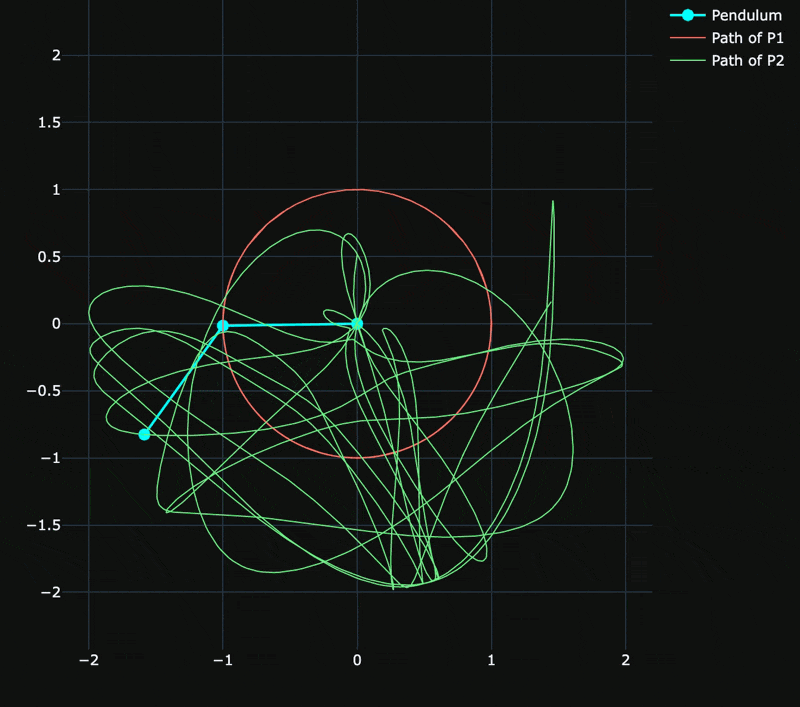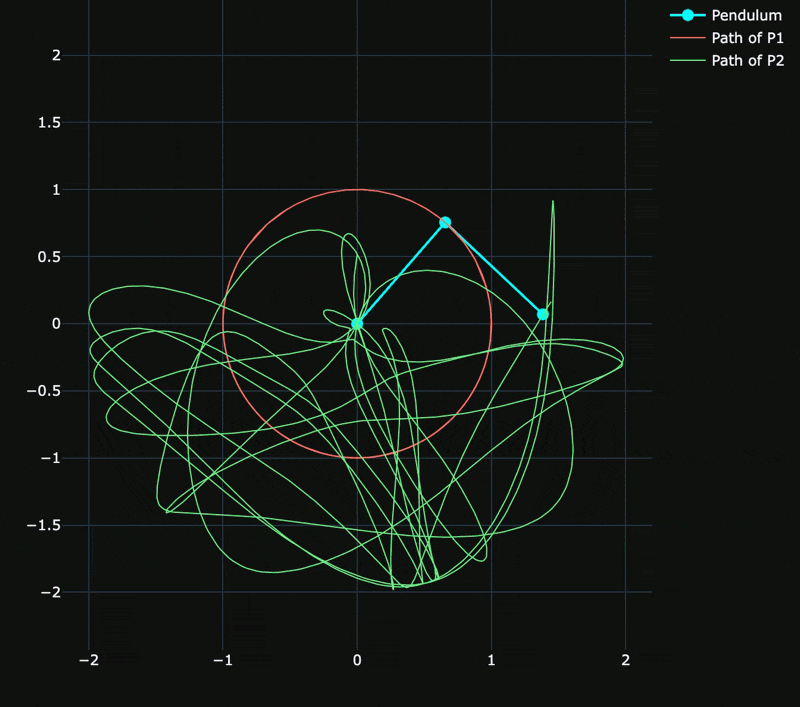
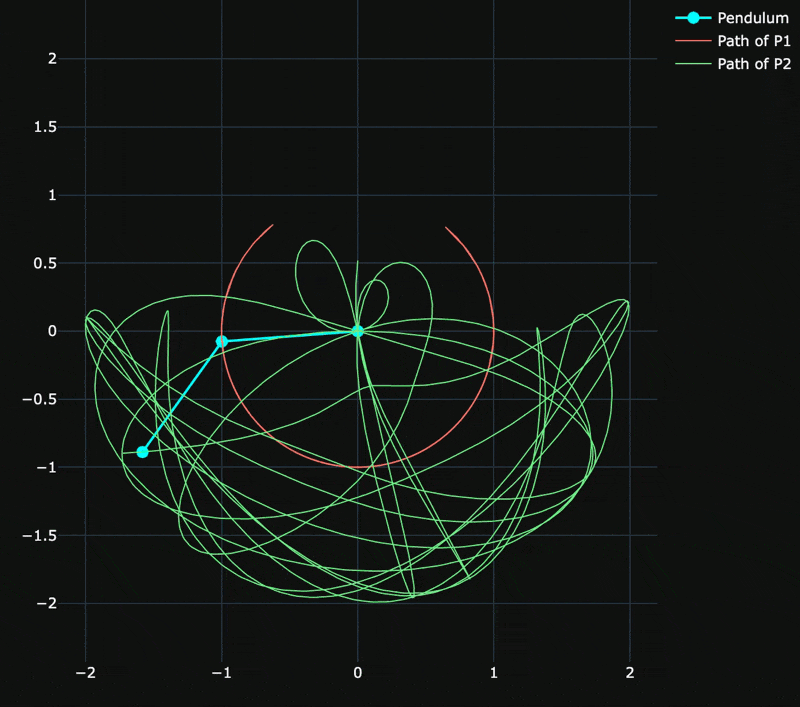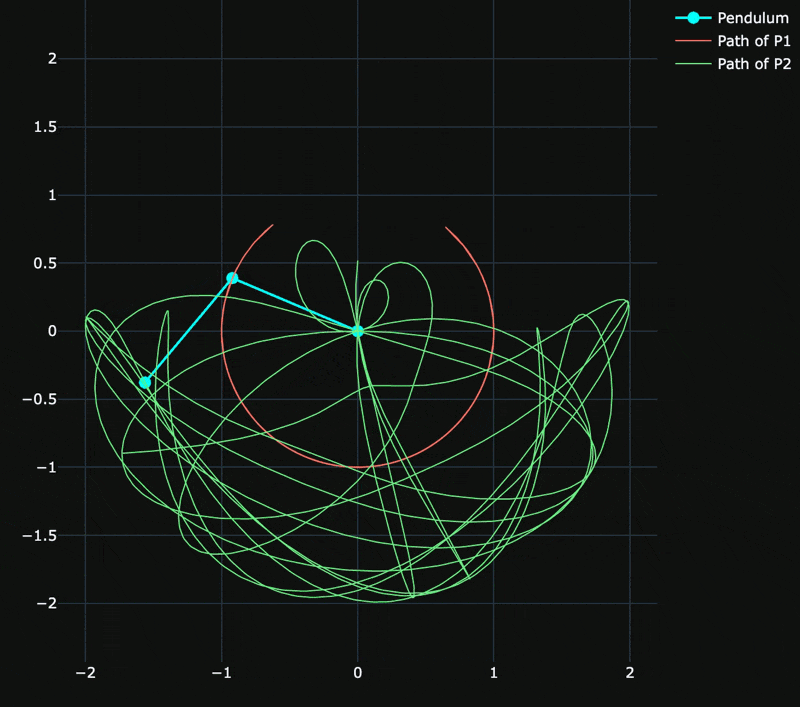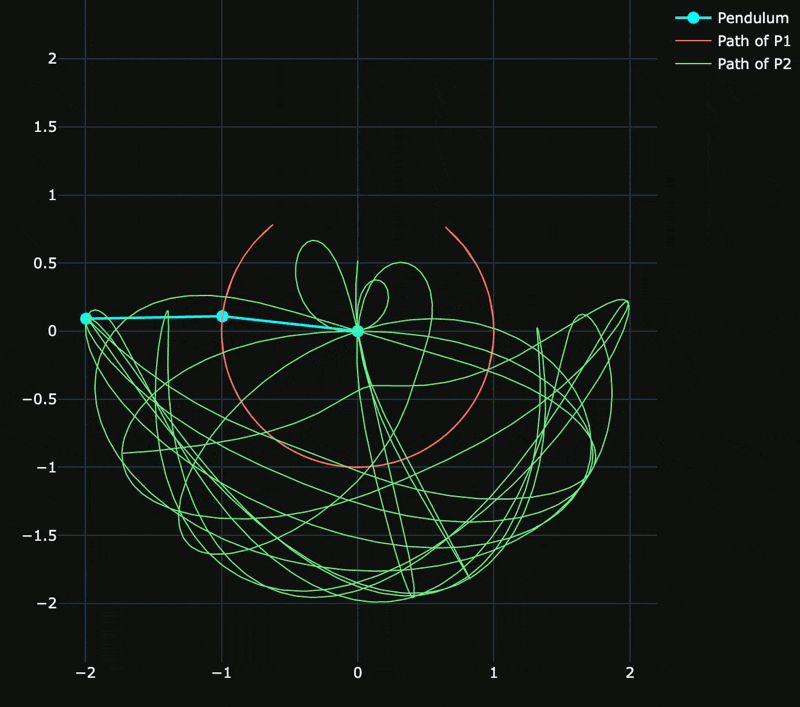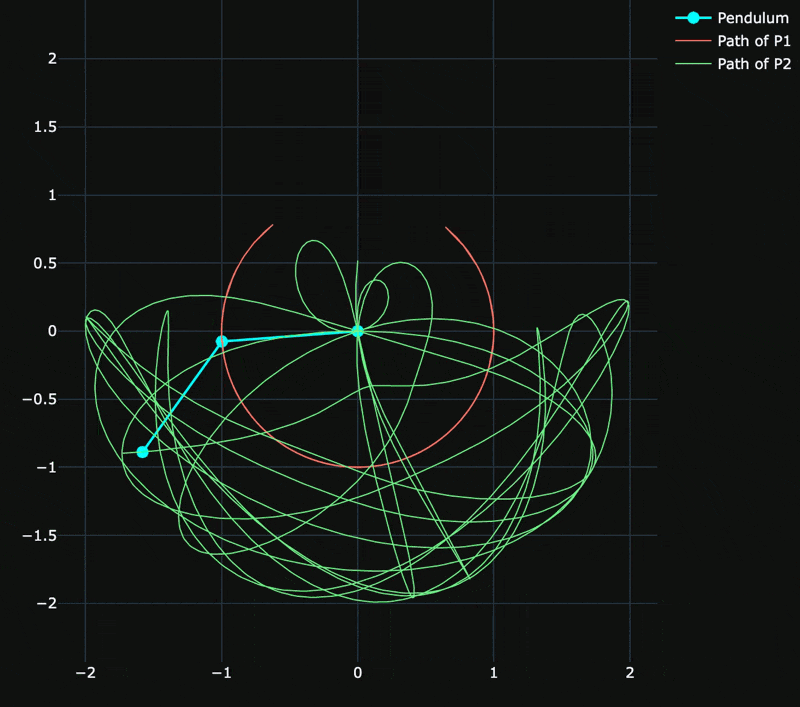
The above figure shows simple pendulum suspended from another simple pendulum by a frictionless hinge.

• Both pendulums move in the same plane.
• In this system, the rods $OP_1$ and $P_1P_2$ are rigid, massless and inextensible.
• The system has two degrees of freedom and is uniquely determined by the values of $\theta_1$ and $\theta_2$

---

We solve the Euler-Lagrange equations for $\textbf{q} = [\theta_1, \theta_2]$ such that,

$$ \frac{\text{d}}{\text{d}t}\left(\frac{\partial L}{\partial \dot{\textbf{q}}}\right)-\frac{\partial L}{\partial \textbf{q}}=0 $$

The result is a system of $|\textbf{q}|$ coupled, second-order differential equations

---

The equations are uncoupled by letting $\omega_i = \frac{\text{d}}{\text{d} t}\theta_i$

So $\omega_i$ for $i=1,2$ represents the angular velocity with $\frac{\text{d}}{\text{d} t}\omega_i \equiv \frac{\text{d}^2}{\text{d} t^2}\theta_i$

Derivation

---

Model rods: Simulation

Systems illustrating periodic/chaotic behaviour are explored.

The gif below shows chaotic motion with release from rest for large initial angles $[\theta_1=-105 \degree, \theta_2=105 \degree]$

---

Rods with non-zero mass: Simulation

The rods $OP_1$ and $P_1P_2$ are now modeled as rigid and inextensible with uniformly distributed mass, $M_1$ and $M_2$. This significantly influences the pendulum dynamics.

Derivation

The gif below shows release from rest for large initial angles $[\theta_1=-105 \degree, \theta_2=105 \degree]$ as above.

In this simulation, the only difference is the mass distribution - uniform along the length;

• $M_1=M_2=1\text{kg}$
• $l_1=l_2=1\text{m}$

---

Update 10/01/2024: Refactored taking OOP approach

Functions_OOP.py

• The utilities in this file abstract the complex symbolic derivation tasks.

Class_OOP.py

• This file defines the DoublePendulum class, encapsulating all aspects of a double pendulum simulation within an object-oriented framework.
• The class allows for the selection of simple or compound pendulum models

Simulation

---

Update 13/01/2024: Dash App deployed

www.double-pendulum.net

See Repository

---

Next steps

• Dynamically creating the trace plot on the animation
  • The method I tried was computational expensive - need workaround
  • Non-functioning work-in-progress code
• Quantifying chaotic behaviour.
  • This will enable me to choose better example and better quantify the range of dynamics

---

---