CControl

CControl is a library written in 100% ANSI C (C89) code. No external libraries and 100% platform independent. The purpose with this library is to fit advanced tools for really small embedded systems or desktop as well. Here I have focused on practical numerical methods and selected the methods that works best in practice. It has been a lot of work finding the best methods and best algorithms.

CLAPACK, Math Kernel Library, FFTPACK support

This library have different types of libraries. First library is the internal lightweight library that suits small embedded systems. The second library is higher lever library for larger matrices. The third library is libraries that are hardware independent. Set this as your math library inside defines.h file. The Math Kernel Library is extremely optimized and it's suitable for operative systems such as Windows, Linux, Mac OS meanwhile the lightweight library or CLAPACK and FFTPACK is suitable for an Arduino, STM32, PIC etc because they are 100% portable. The internal library is suited for really small devices.

Routines	Function	Comment
`ssyevd`	`svd.c`	Singular value decomposition for symmetric matrices
`ssyevd`	`eig.c`	Eigendecomposition for symmetric matrices
`sgeev`	`eig.c`	Eigendecomposition for square matrices
`sgessd`	`svd.c`	Singular value decomposition for general matrices
`spotrf`	`chol.c`	Cholesky facorization for real symmetric matrices
`sgetrf`	`lup.c`	LU factorization with pivoting for square matrices
`sgetrs`	`linsolve_lup.c`	Solve linear system `Ax = b` with LU factorization
`sposv`	`linsolve_chol.c`	Solve linear system `Ax = b` with Cholesky factorization
`sgetri`	`inv.c`	Inverse by using LU factorization for square matrices
`sgeqrf` `sorgqr`	`qr.c`	QR factorization for general matrices
`sgemm` `ssymm` `sgemv` `ssymv`	`mul.c`	Multiplication
`sgesvd`	`pca.c`	Principal component analysis
`sggev`	`eig_generalized.c`	Generalized eigenvalue problem for non-symmetric matrices
`ssygvd`	`eig_generalized.c`	Generalized eigenvalue problem for symmetric matrices
`rfftf`	`fft.c`	Compute Fast Fourier Transform 1D
`cfftb`	`ifft.c`	Compute Inverse Fast Fourier Transform 1D
`rfftf`	`fft2.c`	Compute Fast Fourier Transform 2D
`cfftb`	`ifft2.c`	Compute Inverse Fast Fourier Transform 2D

If you want to add more, just download clapack-3.2.1.zip from Netlib and include necessary .c files inside the Lapack folder of this project, for supporting your routine.

Type	Internal	MLK	CLapack	FFTpack
`Speed`	Slow for large data	Fast for large data	Faster than internal	Very fast
`Portability`	Platform independent	Only Windows/Linux/ Mac OS	Platform independent	Platform independent
`Missing`	Eigenvectors for general matrices	Nothing	Nothing	Nothing
`Memory requirements`	Lightweight	Large	Medium	Lightweight

Main focuses are:

Artificial Intelligence
- Astar algorithm for quick path finding
- Point-in-polygon algorithm for checking if a point is inside the area
Machine Learning
- Sobel FAST Angle Object Detection (SFAOD)
- Local Binary Pattern (LBP)
- Sobel FAST Angle (SFA)
- Fisherfaces with pooling, Kernel PCA, LDA and Neural Network for image classification and object detection
- Density-Based Spatial Clustering of Applications with Noise
- Support Vector Machine
- Kernel for PCA and LDA
- Neural network
- Kernel Principal Component Analysis
- K-means clustering
Control Engineering
- Kalman filter update
- Linear Quadratic Integral regulator
- Model Predictive Control (Ongoing)
- Model Reference Adaptive Control
- Transfer function to state space
- Stability check
- Continuous to discrete
Image Processing
- Gaussian filtering for images
- Robust Principal Component Analysis
- Sobel filter
- Portable Gray Map (PGM) reader, print and free
- Image resize
- Pooling Max, Average and Shape
- Features From Accelerated Segment Test (FAST)
- Hough Transform for line detection
- Harris corner detection
- Orientation of a matrix by using Intensity Centroid
Signal Processing
- Fast Fourier Transform Shift
- Fast Fourier Transform 1D
- Fast Fourier Transform 2D
- Inverse Fast Fourier Transform Shift
- Inverse Fast Fourier Transform 1D
- Inverse Fast Fourier Transform 2D
- Particle filter
- Cluster filter
- Filtfilt
- Square Root Unscented Kalman Filter
Linear Algebra
- Balance matrix
- Cholesky decomposition
- Cholesky update
- QR decomposition
- LUP decomposition
- Determinant
- Discrete Lyapunov solver
- Eigenvalues and eigenvectors
- Generalized eigenvalue problem
- Hankel matrix
- Inverse
- Dot product
- Pseudo inverse
- Linear solver
- Nonlinear solver
- Multiplication
- Singular Value Decomposition
- Transpose
- Norm
- Matrix exponential
- Rank
- Convolution matrix
Miscellaneous
- Angle of two vectors
- Concatenate
- Cut matrix
- Find
- Matrix symmetric check
- Insert sub matrix into matrix
- Pdist2
- Popcount
- Print matrix or vector
- Saturation
- Sign
- Value min
- Value max
- Sort
- Sum
Optimization
- Linear programming
- Non-Negative Least Squares
- Quadratic programming
Statistics
- Principal Component Analysis
- Linear Discriminant Analysis
- Randn
- Mean
- Average of the elements inside a form e.g circle
- Max
- Standard deviation
- Variance
- Covariance
- Center
- Ordinary Procrustes Analysis
- Compute centroid of a cluster
- Cluster distance
- Cluster ratio
System Identification
- Observer Kalman Filter identification
- Eigensystem Realization Algorithm
- Recursive Least Square with forgetting factor and kalman filter identification
- Square Root Unscented Kalman Filter for parameter estimation

/*
 ============================================================================
 Name        : Main.c
 Author      : <Your Name Here>
 Version     : 1.0
 Copyright   : MIT
 Description : Initial template
 ============================================================================
 */

#include "CControl/ccontrol.h"

int main() {
	clock_t start, end;
	float cpu_time_used;
	start = clock();

	/* Your ANSI C logic here - All examples can be found at the folder src/CControl/Documents/Examples */

	end = clock();
	cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
	printf("\nTotal speed  was %f\n", cpu_time_used);


	return EXIT_SUCCESS;
}

Projects made with CControl

Fan Controller with Linear Quadratic Integral Control

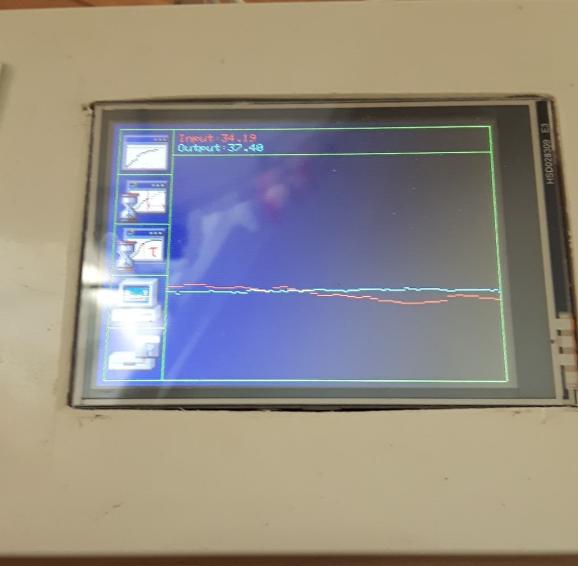
I have created a controller for a fan. The controller works as it read the temperature sensor and it compare the temperature sensor with the potentiometer, which is the reference set point. If the error is large between the temperature sensor and the potentiometer, then the fan is going to turn on high, or low, depending on if the error is negative or positive.

The goal with this system is that I'm going to implement this on a heat source. The fan is going to blow warm air onto a object and the object is holding the temperature sensor. If the fan is blowing to much warm air, then the controller is going to turn down the speed of the fan so the temperature of the object meets the reference

I have been using Matavecontrol and Mataveid to estimate and creating the kalman gain matrix and the LQR control law with integral action. I'm the author of both Matavecontrol and Mataveid.

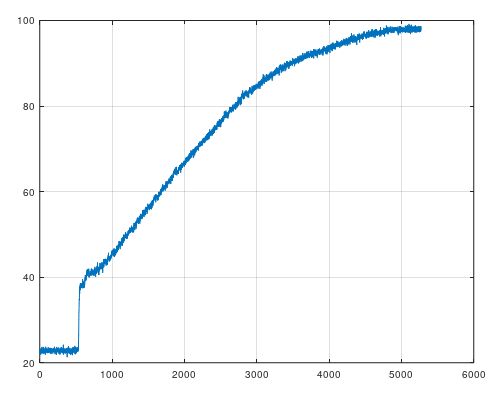
Identification process. Here I have using the Observer Kalman Filter Identification and Eigen System Realization methods.

Simulation process:

Model Predictive Integral Temperature Controller

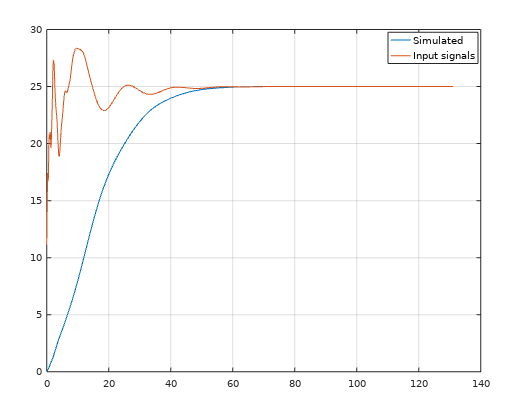
This is a Model Predictive Controller, with integral action. It uses linear programming instead of quadratic programming for the optimization. This controller works well.

This predictive controller have a wiring diagram if you want to build the same controller for your temperature project.

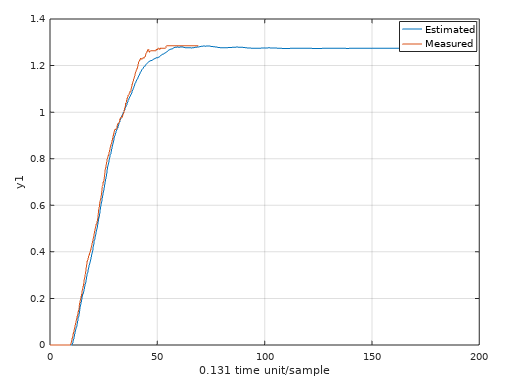
Step answer of first order model.

Model Reference Adaptive CAN-bus controller

This is a MRAC project, Model Reference Adaptive Controller. This controls the a Sonceboz stepper motor with CAN-bus J1939-21 protocol. The purpose is to control a big wheel with two multivariable hydraulical valves.

See the movie in the project folder.

Library for SAE J1939 https://github.com/DanielMartensson/Open-SAE-J1939

Square Root Uncented Kalman Filter for state estimation and parameter estimation

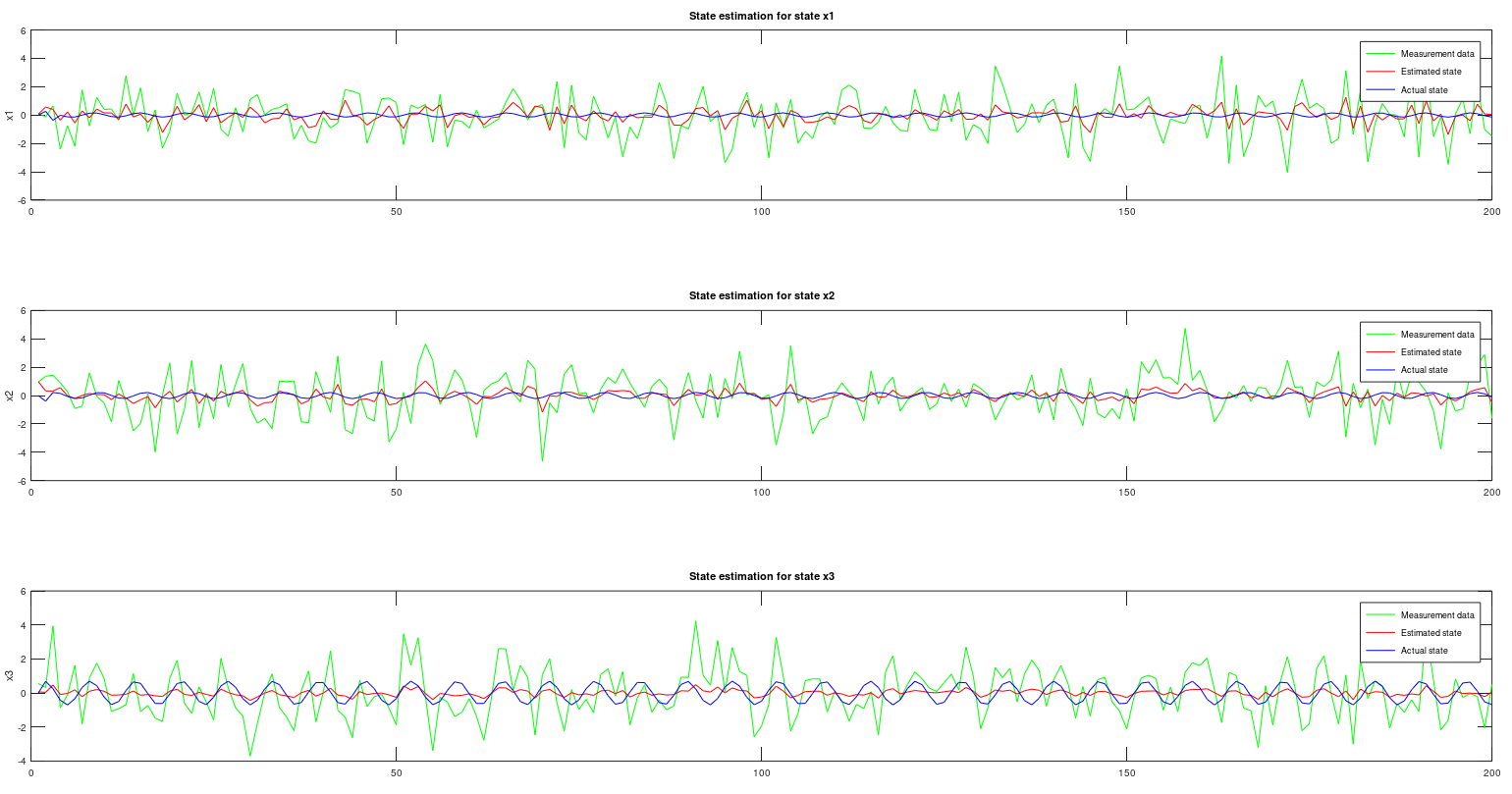
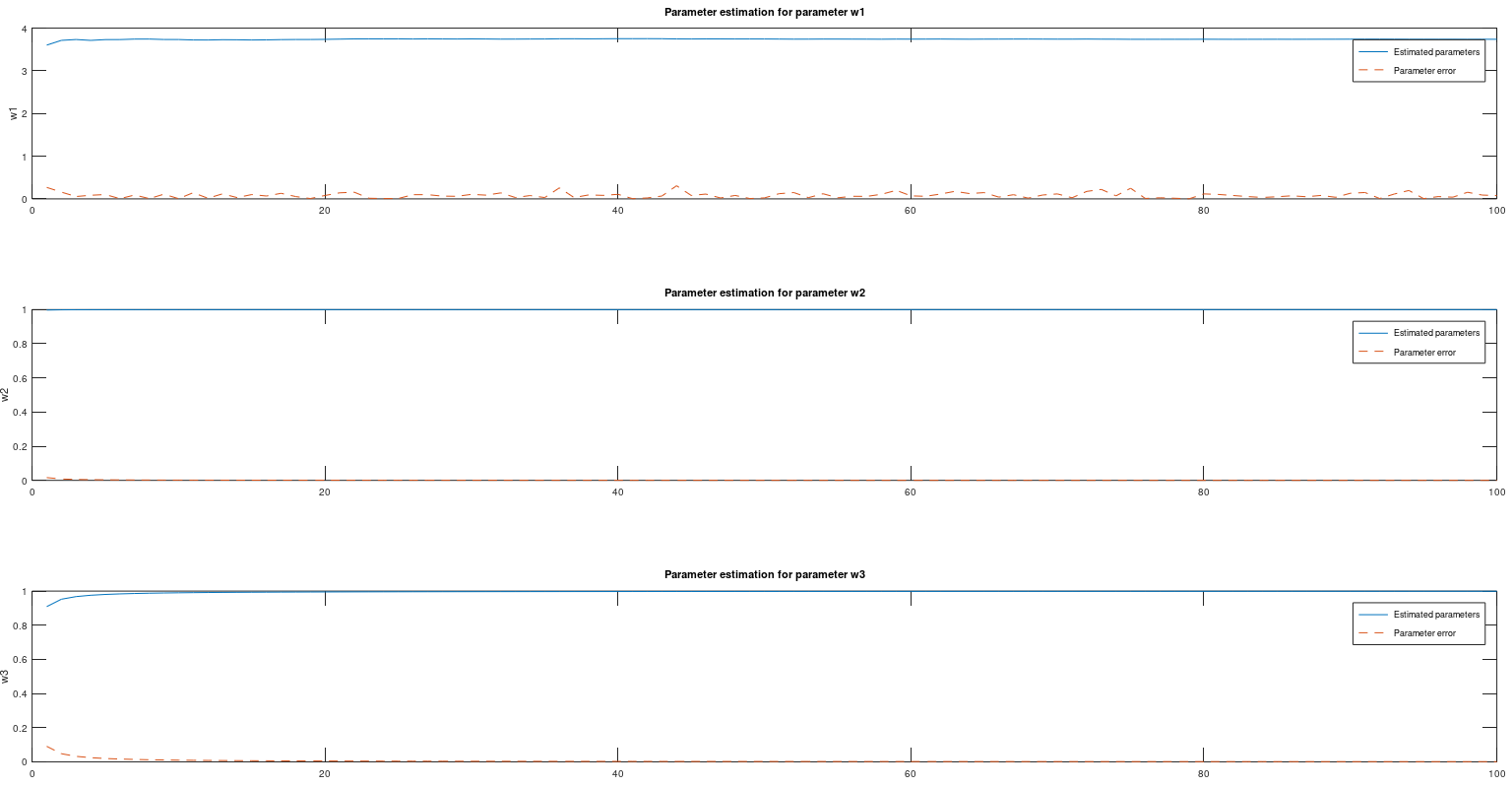
This is the latest Uncented Kalman Filter. MATLAB is using the same algorithm. A .m file is available at the SR-UKF folder.

For state estimation

For parameter estimation

How to use this library with Eclipse CDT

I have made so both Microsoft Visual Studio users and Eclipce CDT can use this library without conflicts. Here is a tutorial how to configure your Eclipse CDT for this repository.

I'd recommend Eclipse IDE for compiling this software. Eclipse IDE is a very boring IDE, but it's robust and trustable. The Eclipse IDE is always going to be available for you.

Once you have Eclipse IDE installed. Show Git perspective.

Select Git

Copy ssh

Clone git. Just press next and end with finish

Import project

Show view

Select Git staging

Every time you change a file and you want to update your repository

If you don't have a C-compiler, here is a video how to set up a compiler
Begin with your main.c file. Then go to src/CControl/Documents/Examples/ and select a .txt file and paste it into main.c file and press
If you got problem with push your updates to this repository, the you need to configure your authorization. See this link

ppadc/CControl