关于论文D. Q. Mayne, M. M. Seron, and S. V. Raković, “Robust model predictive control of constrained linear systems with bounded disturbances,” Automatica, vol. 41, no. 2, pp. 219–224, 2005.中仿真部分的复现。此外,还加入了LQR和线性MPC的对比案例。
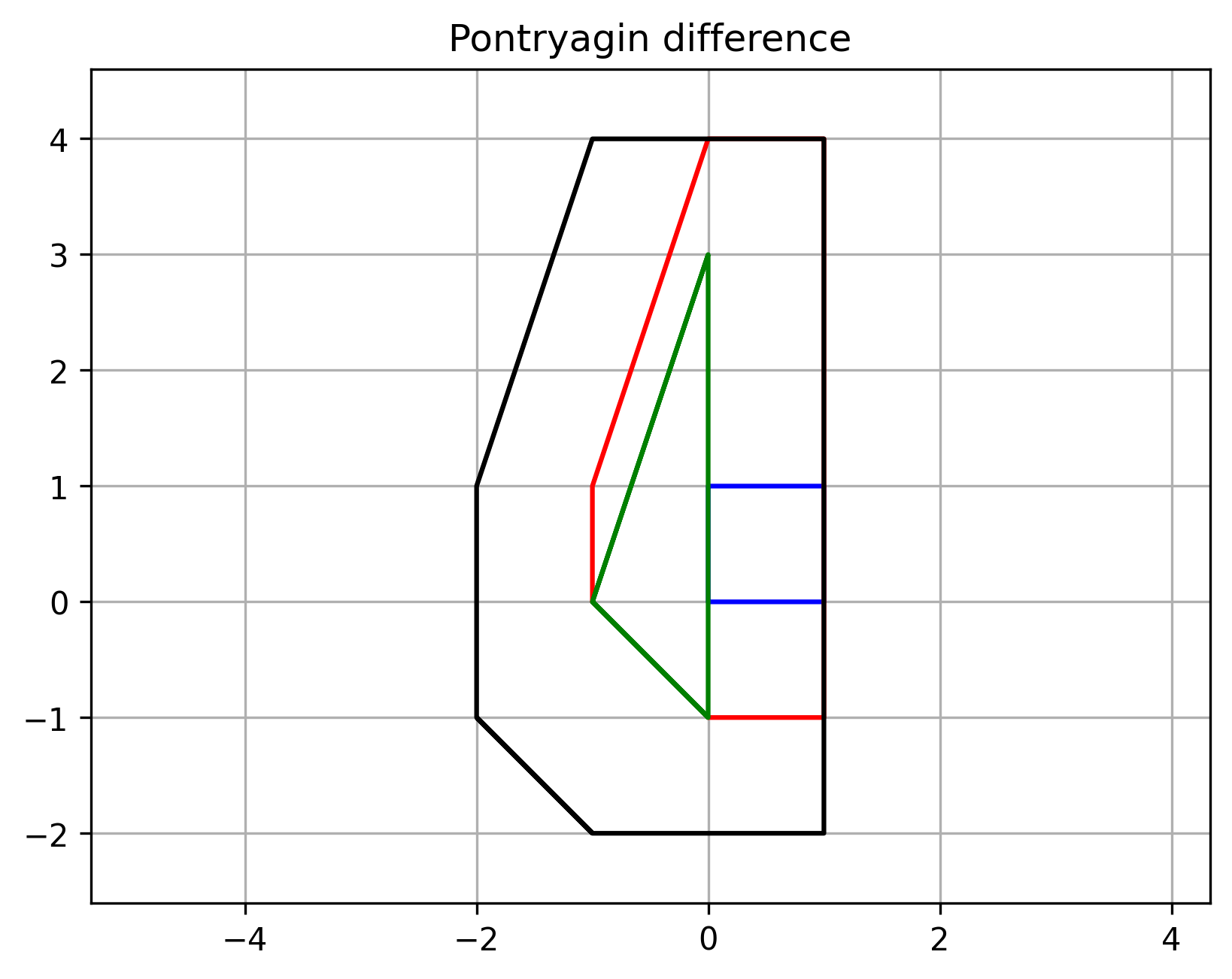
下图表示庞特里亚金差不是将集合内所有向量取反再闵可夫斯基和
实际可以进行升维和降维,这里未展示
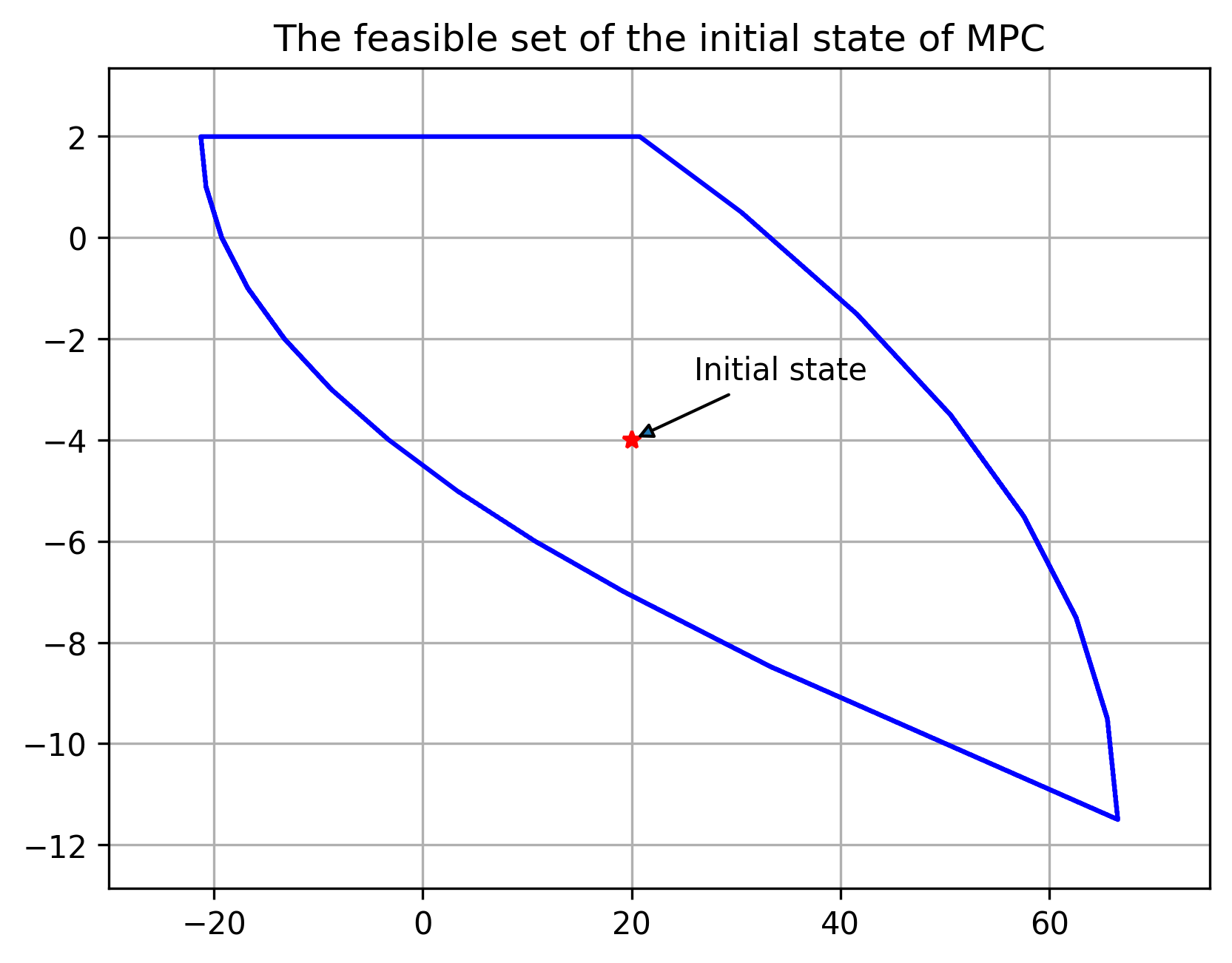
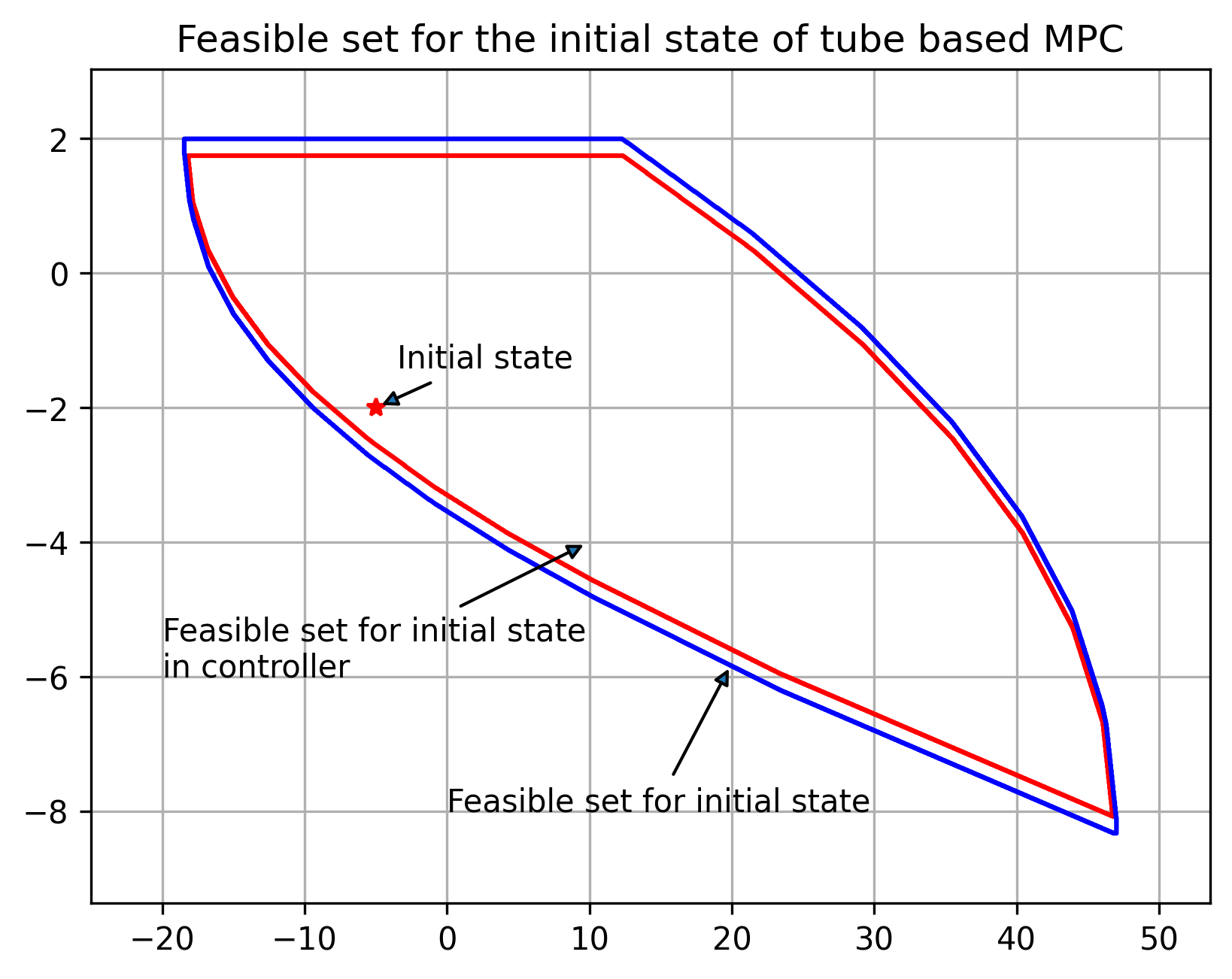
初始状态属于这个集合问题才可解
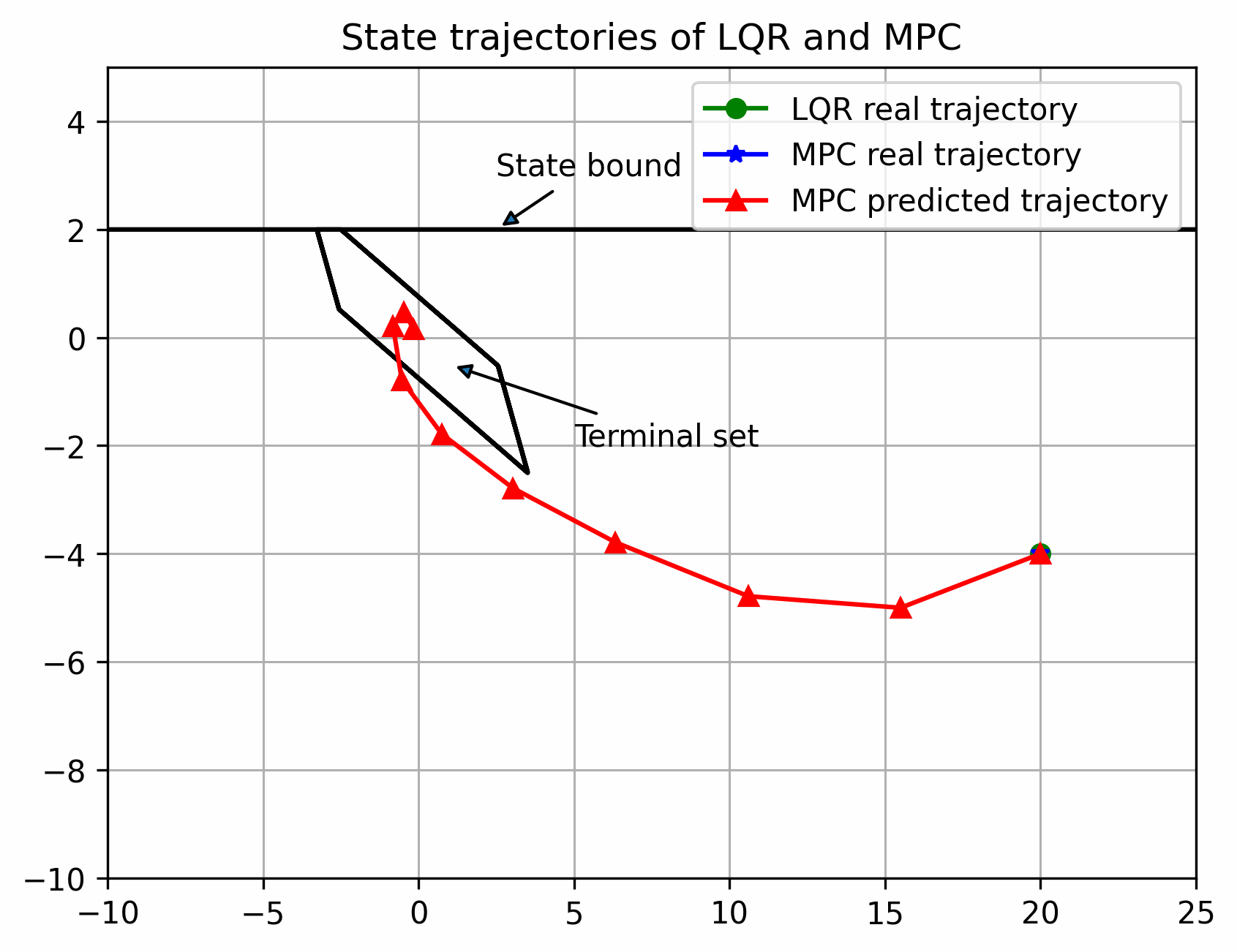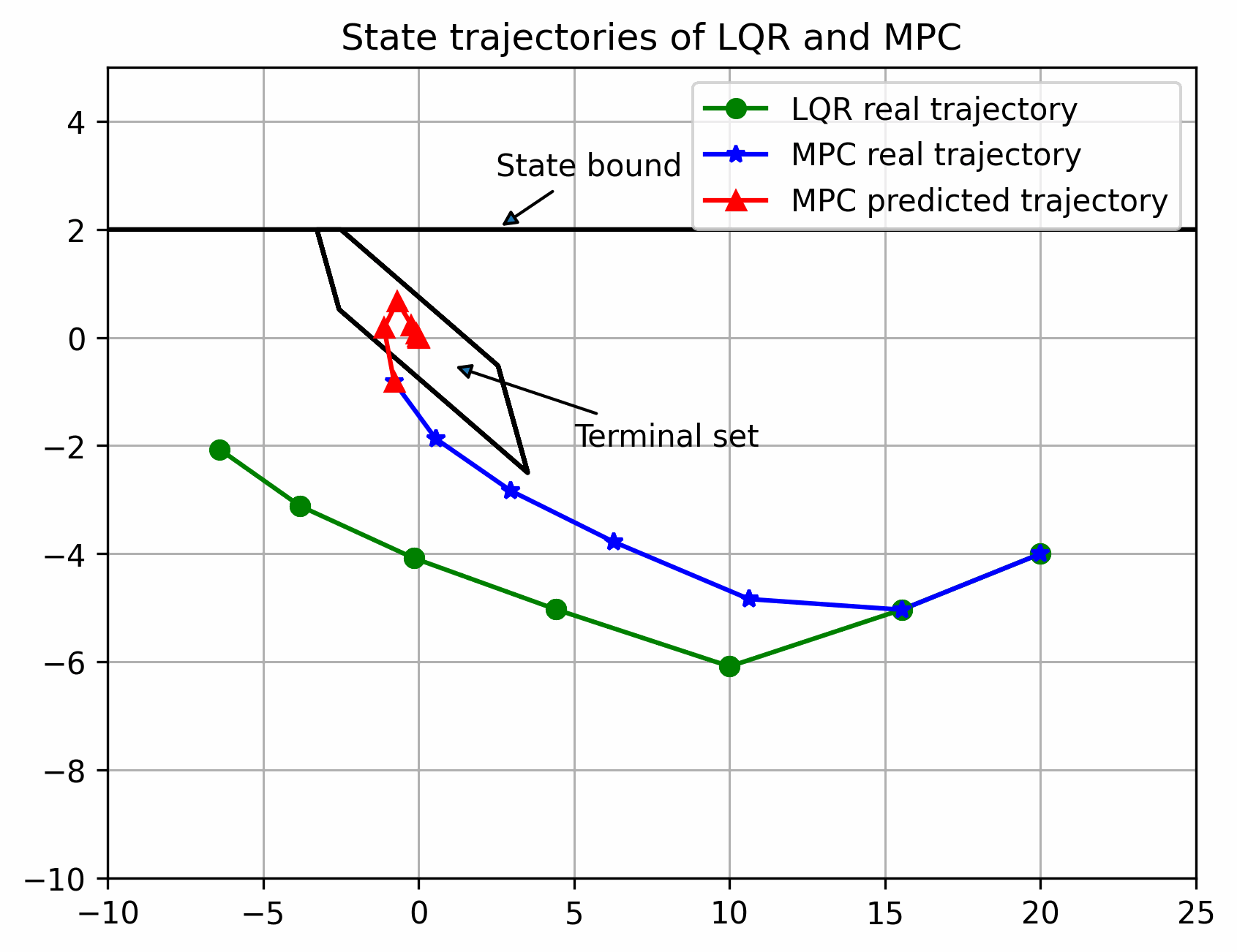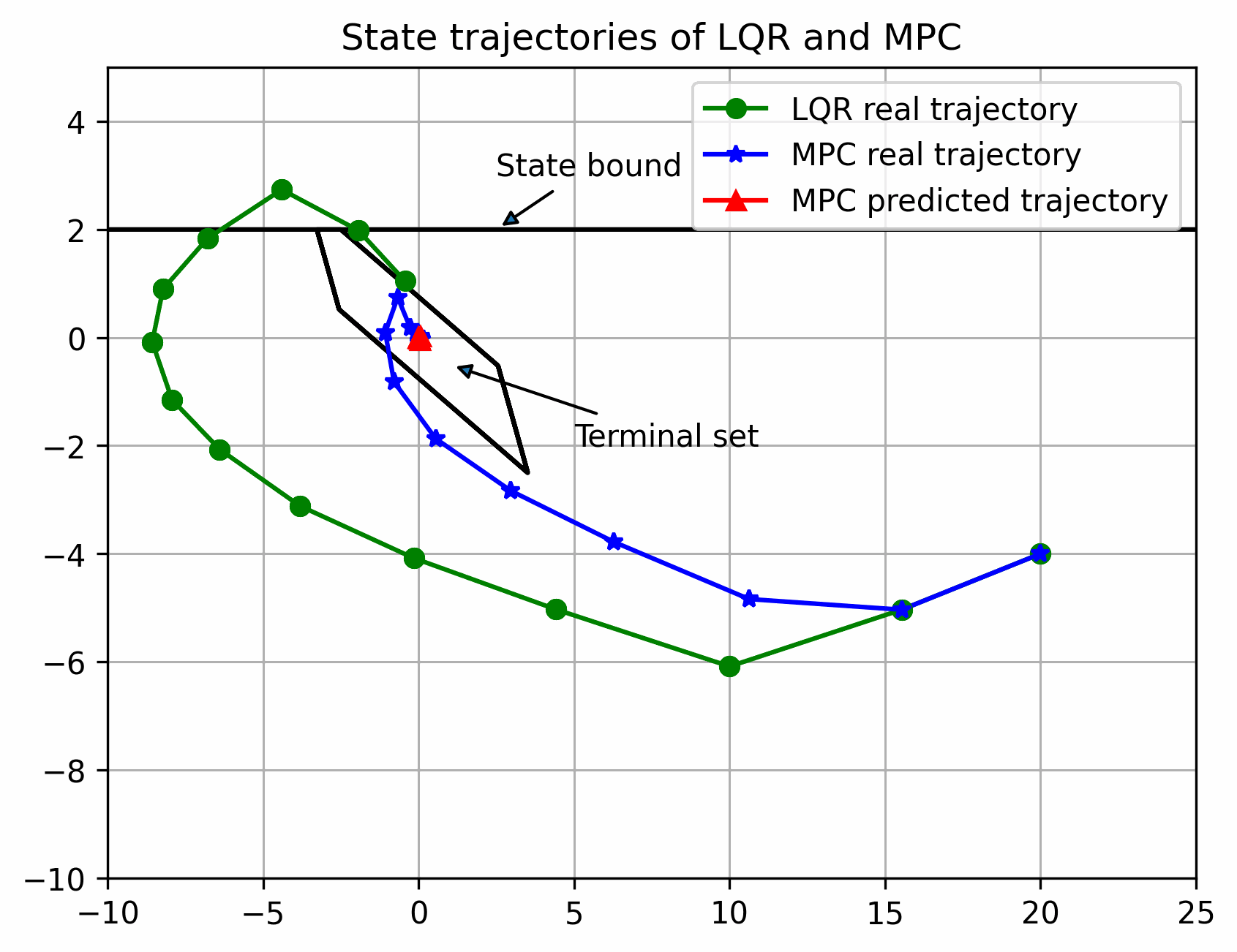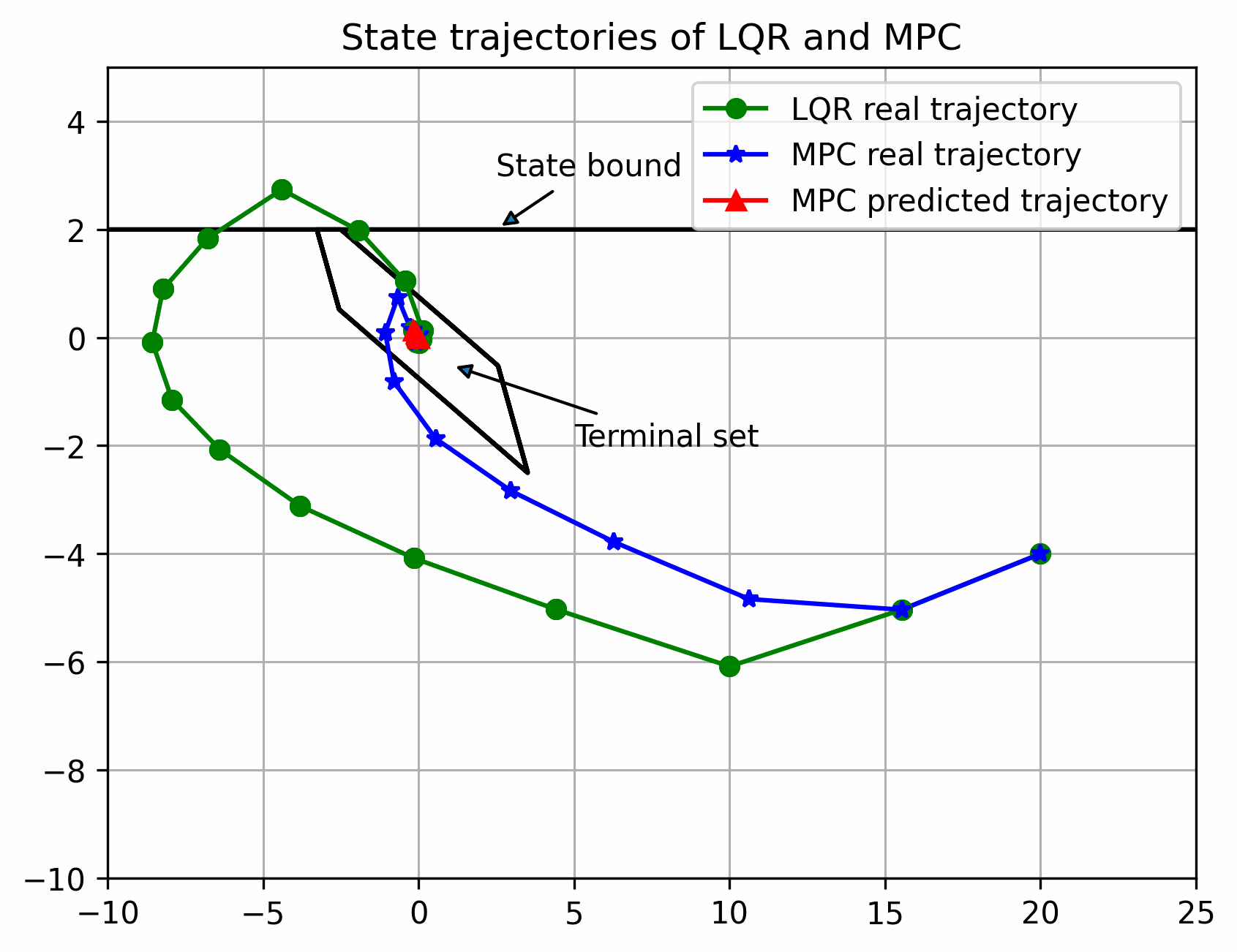
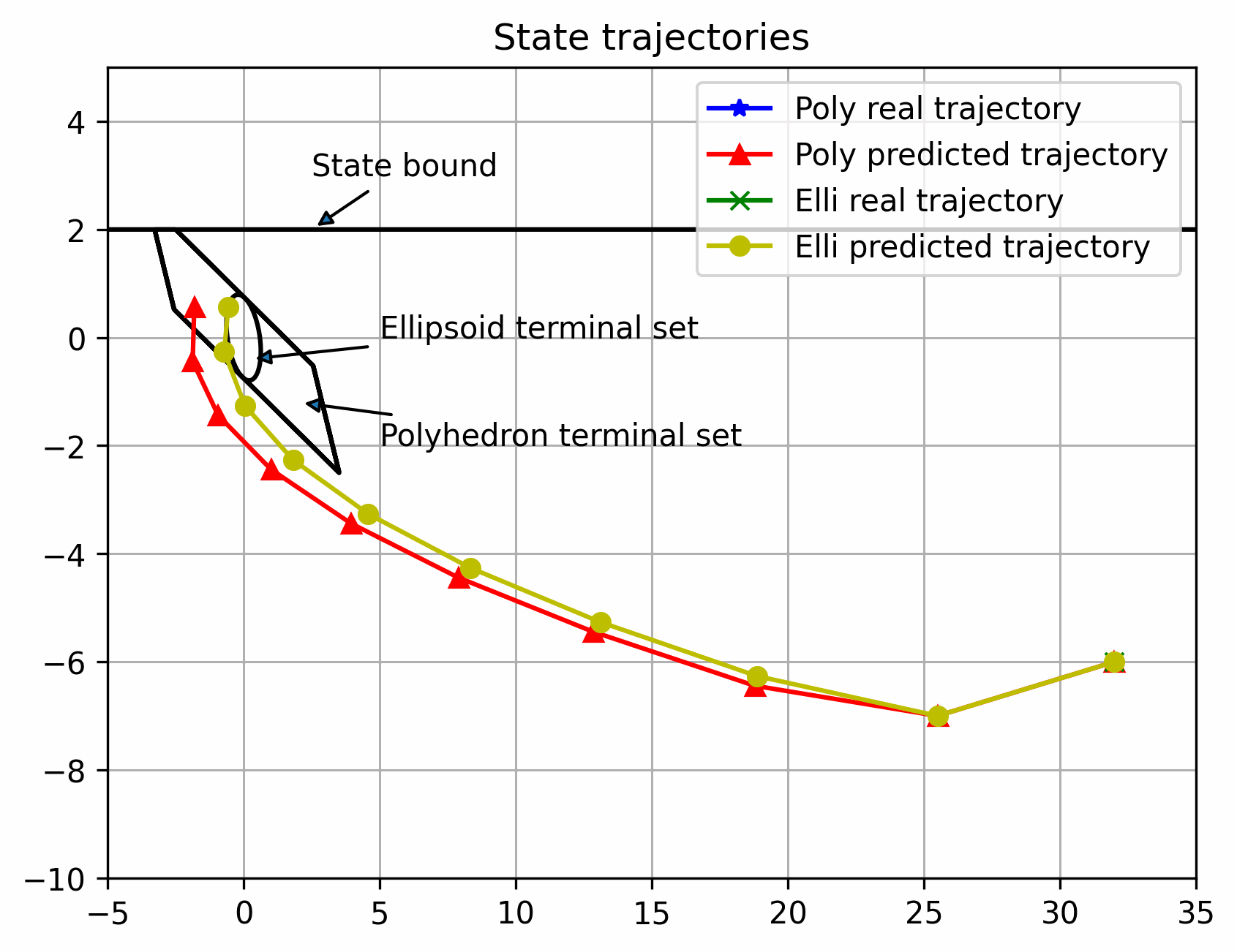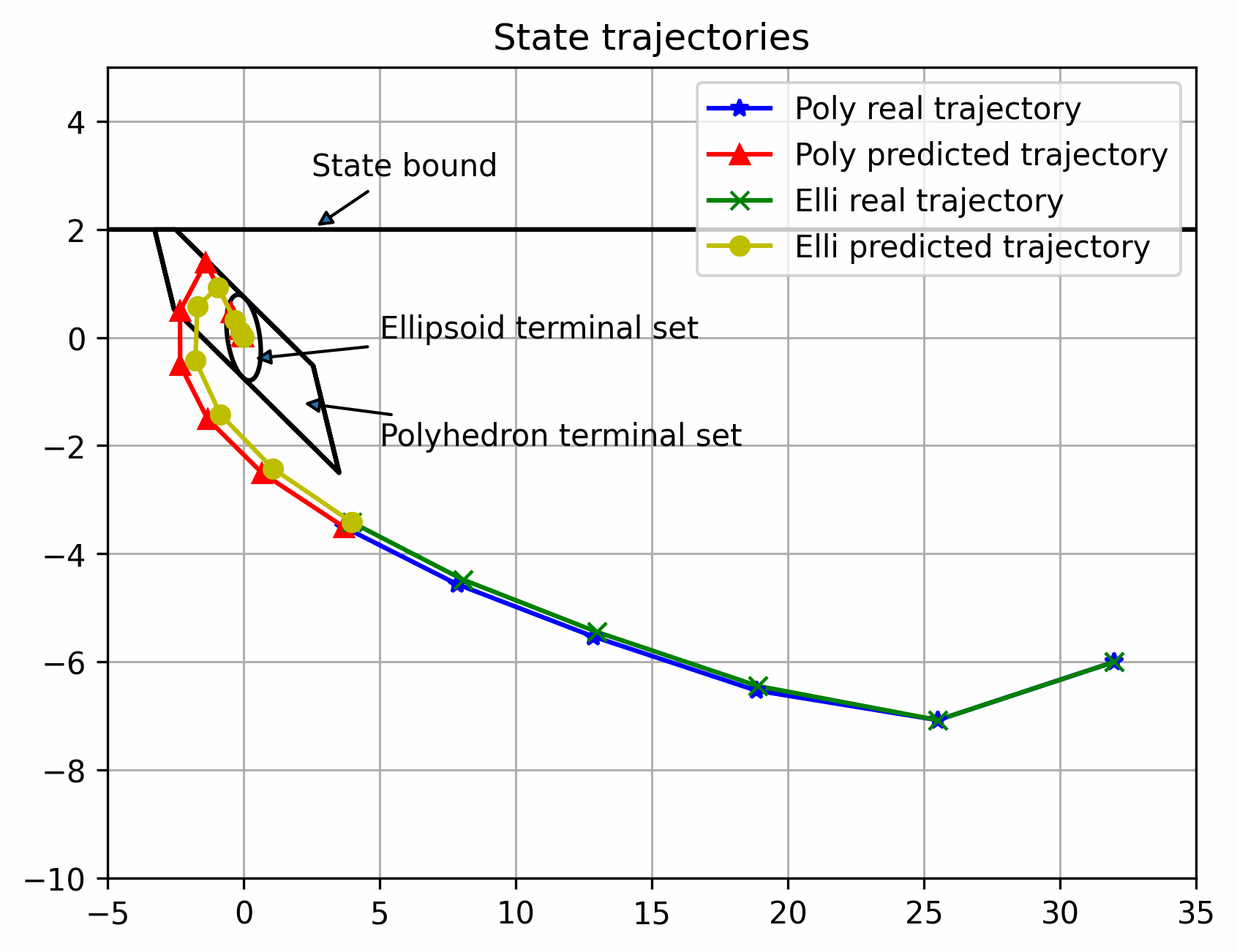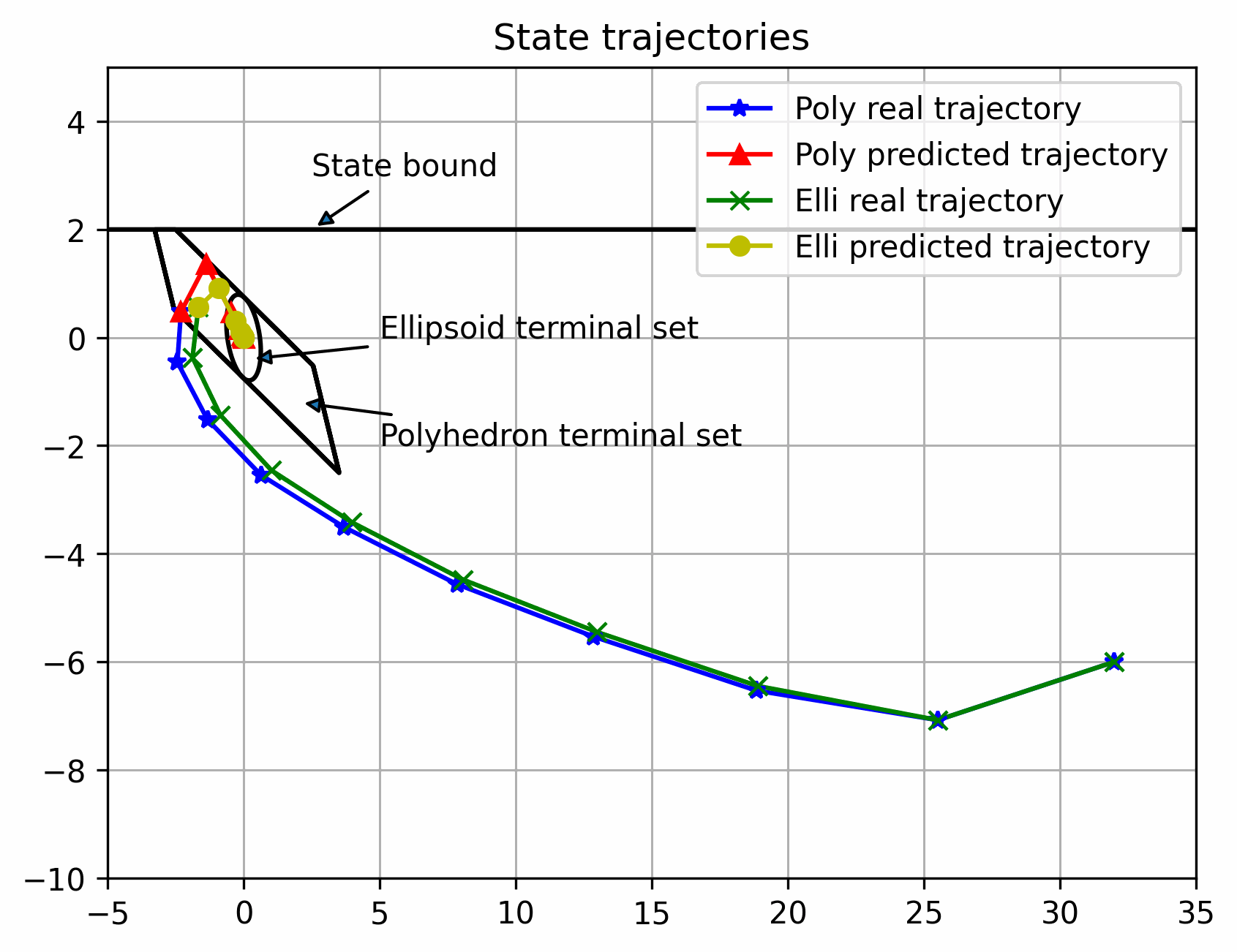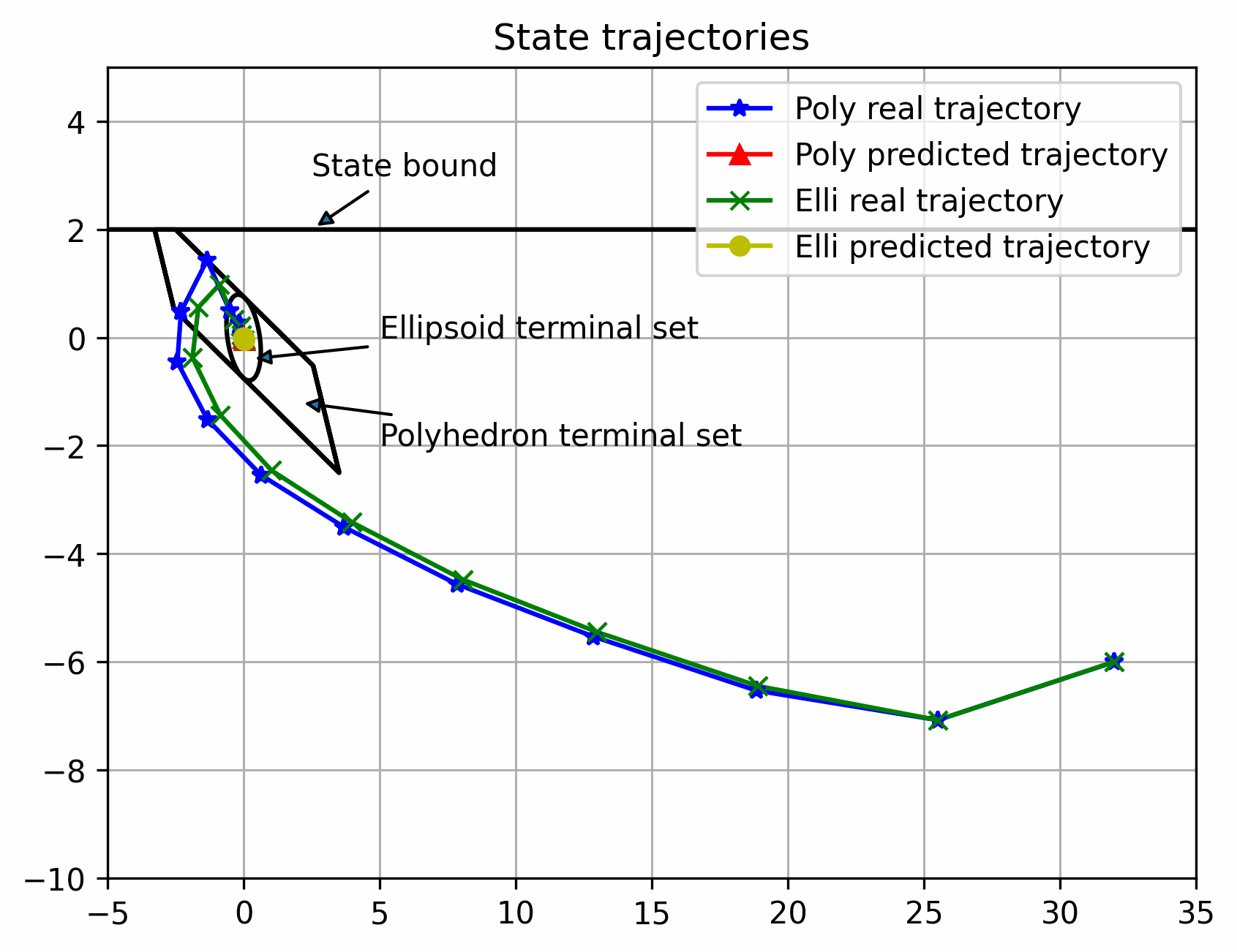
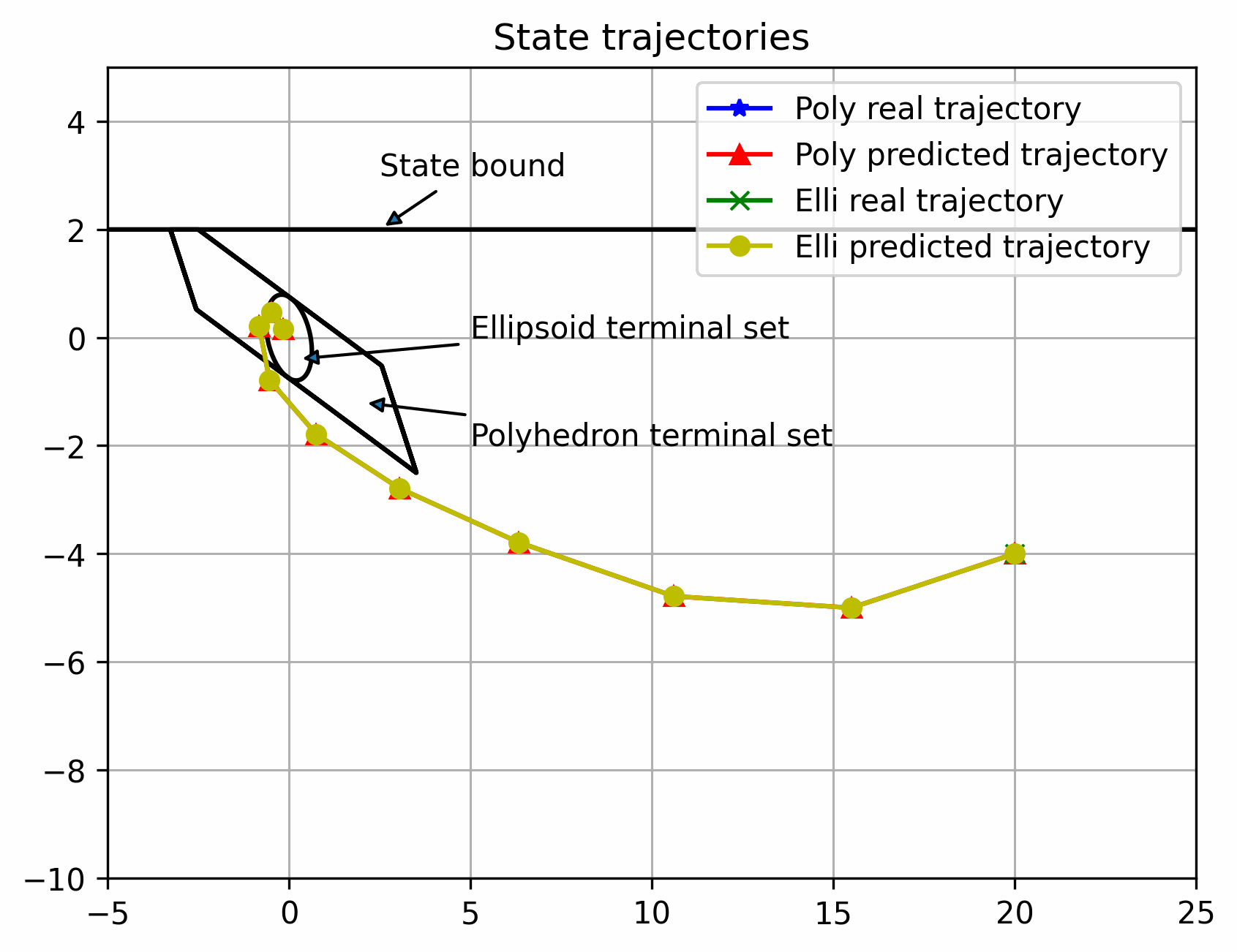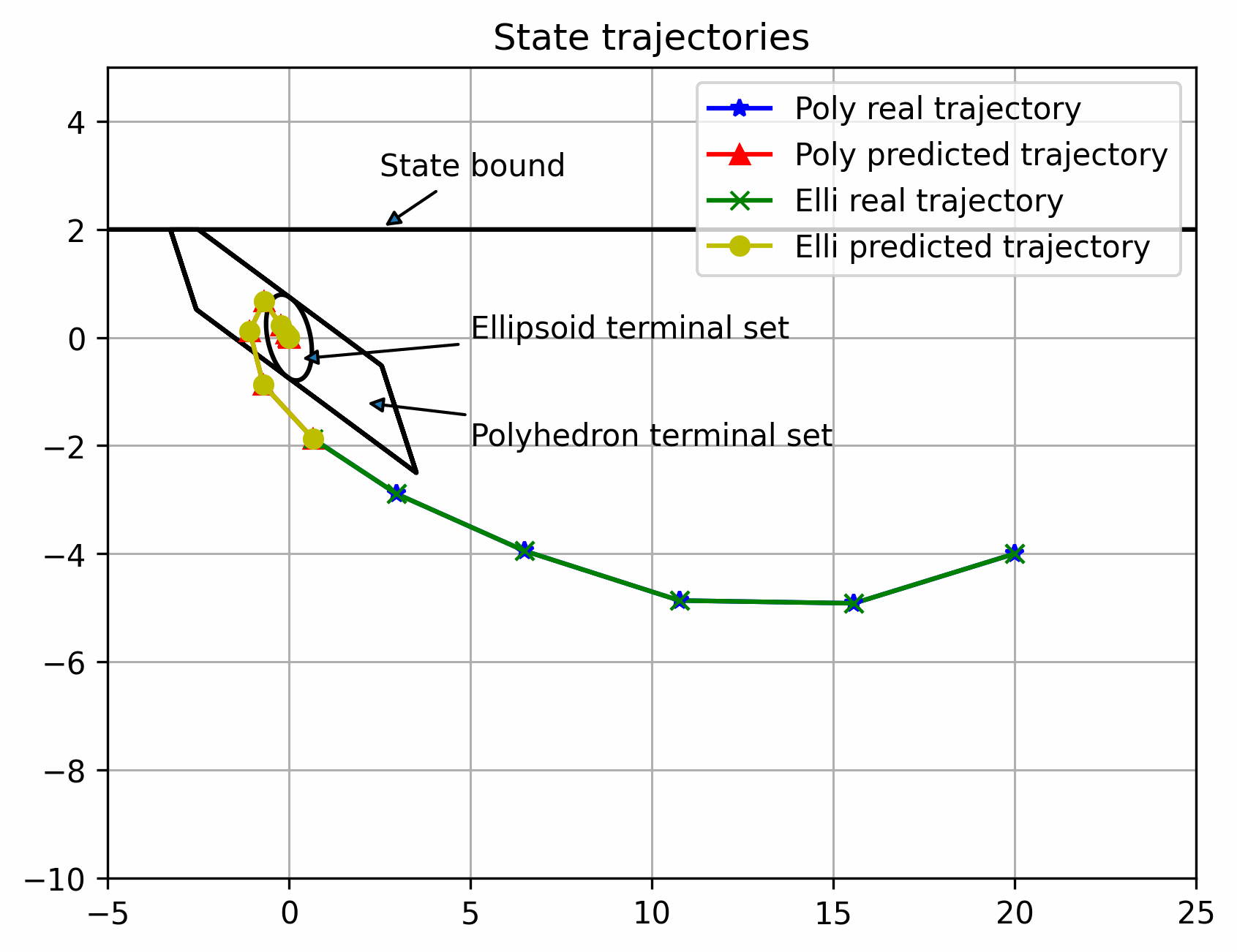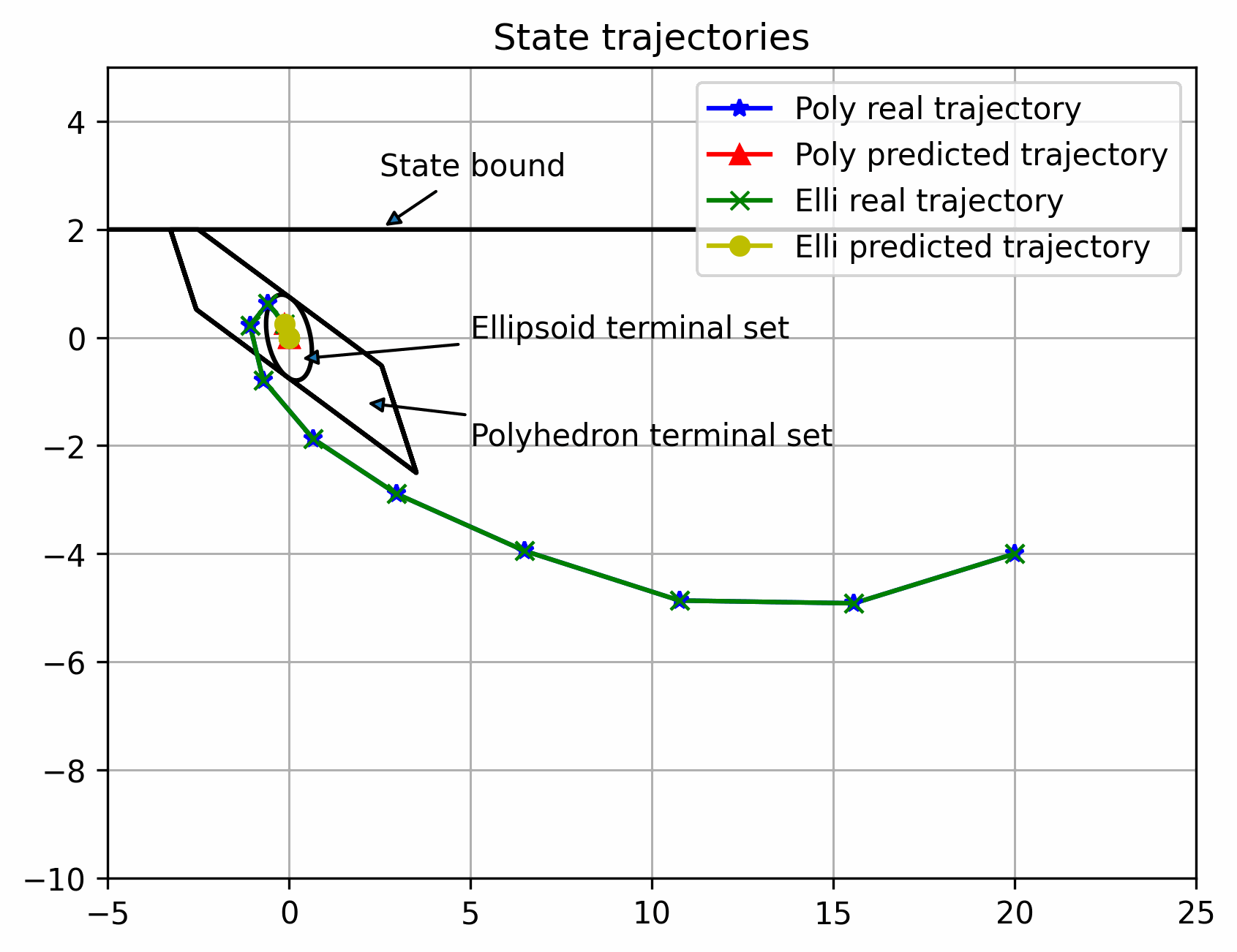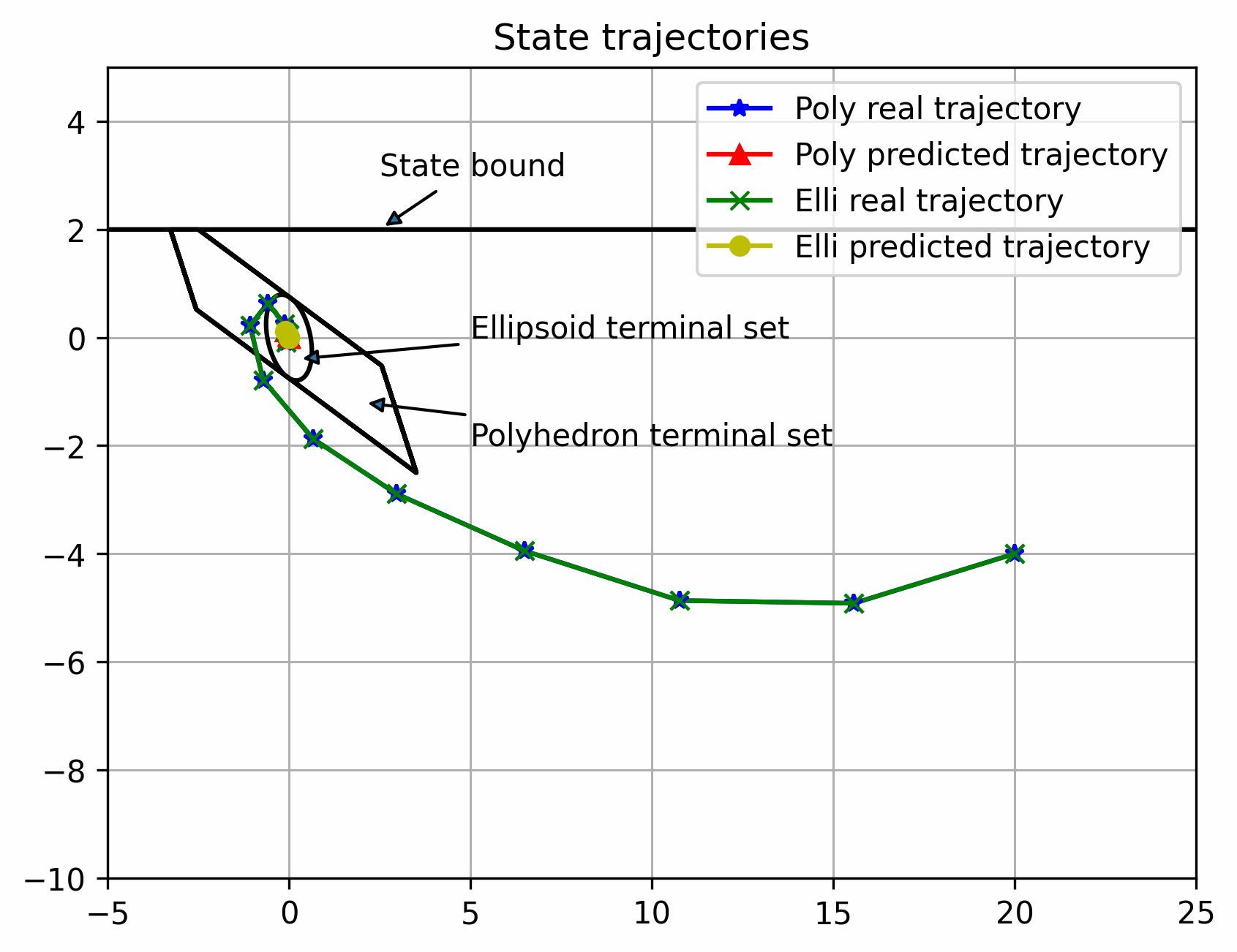
可以看出离稳定点越远,区别越大,反之越小,但都可以稳定(多面体终端集初始可行域更大)
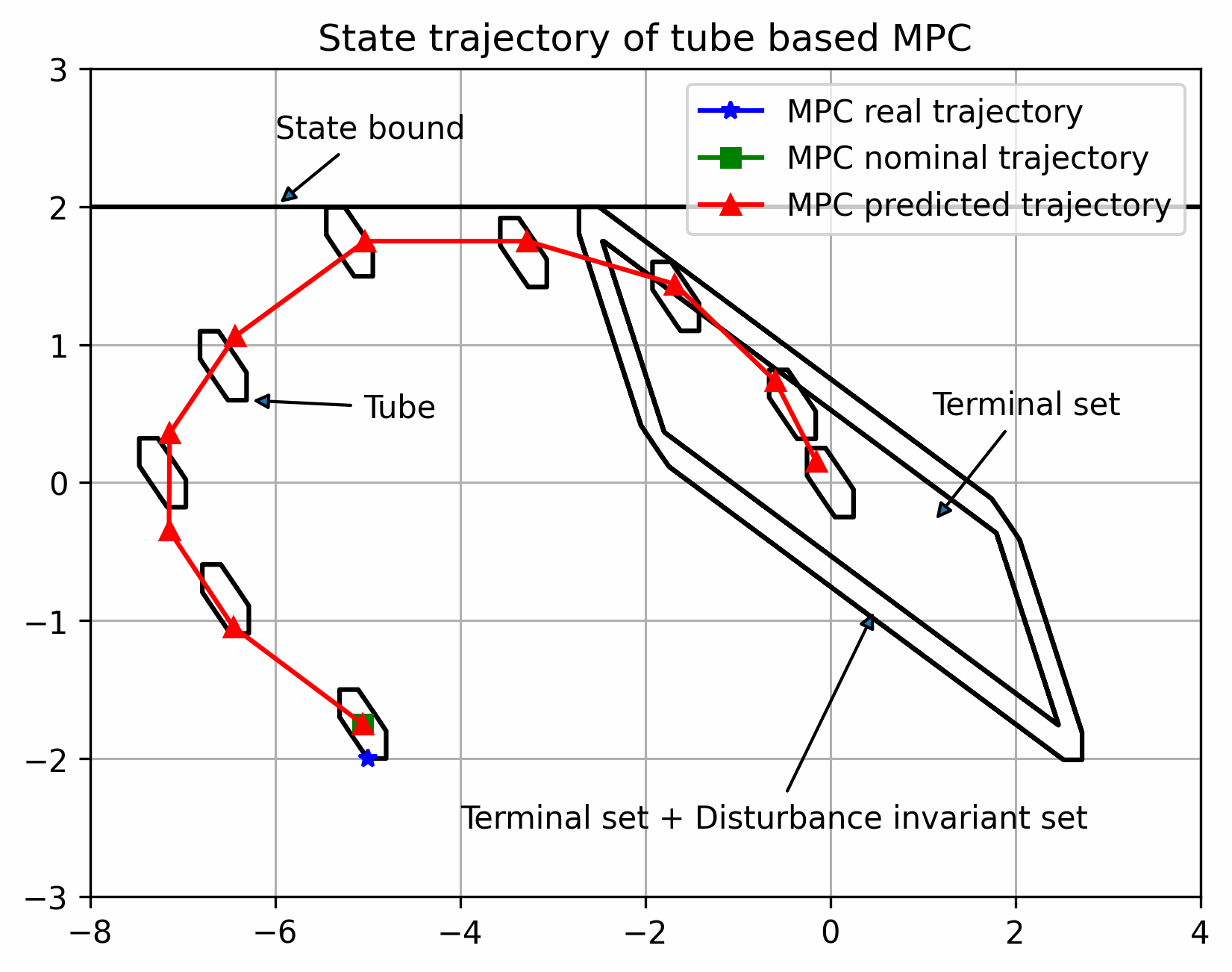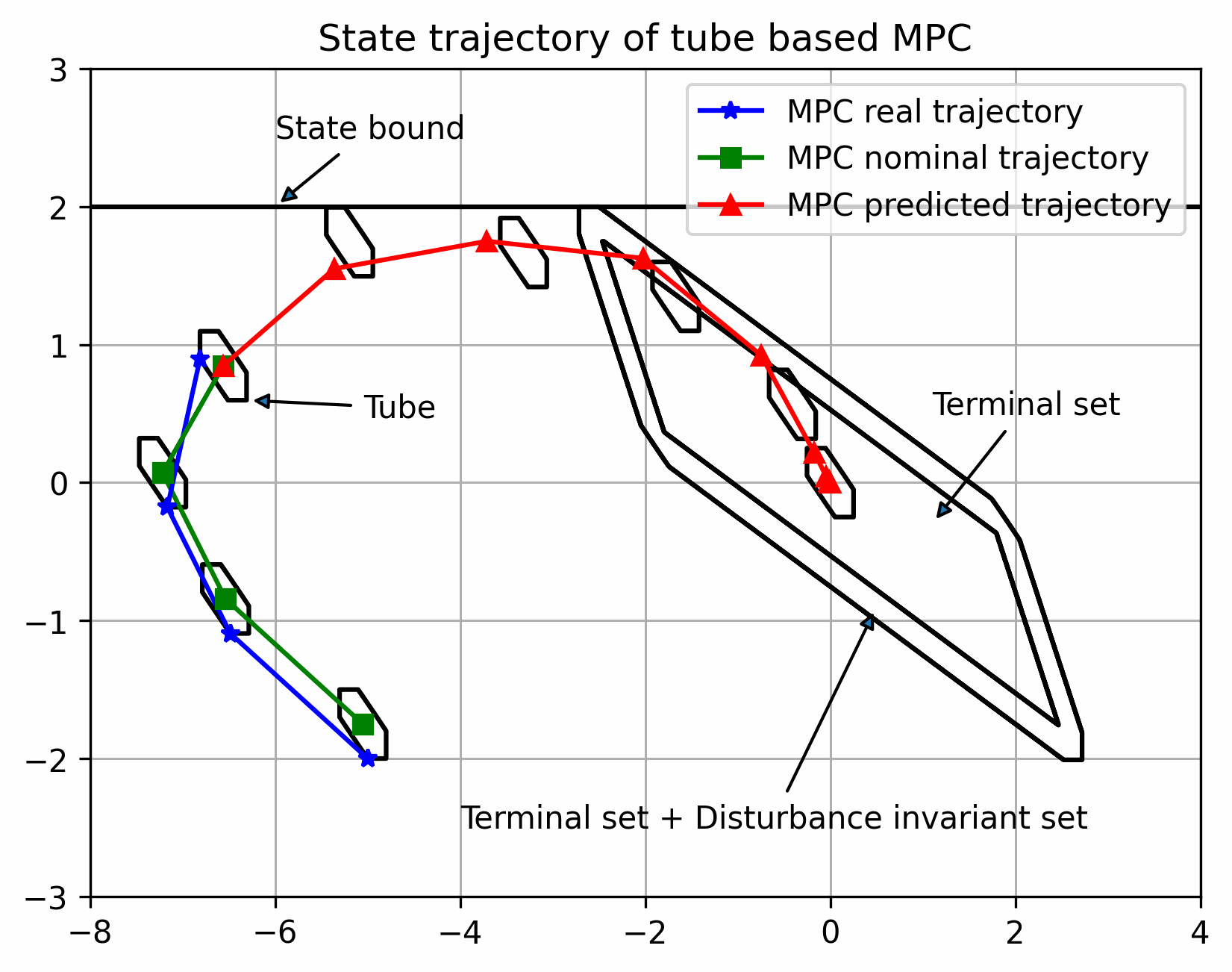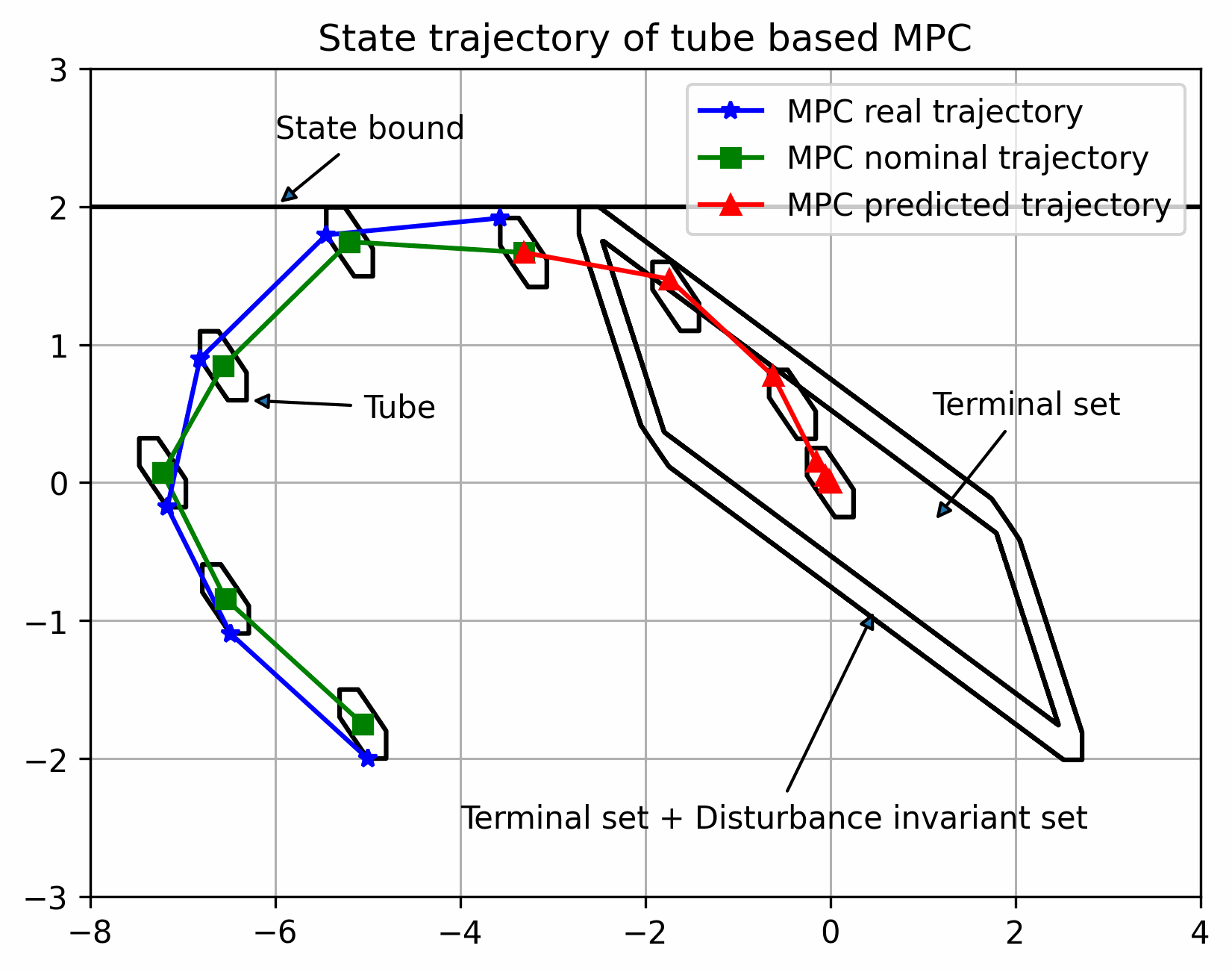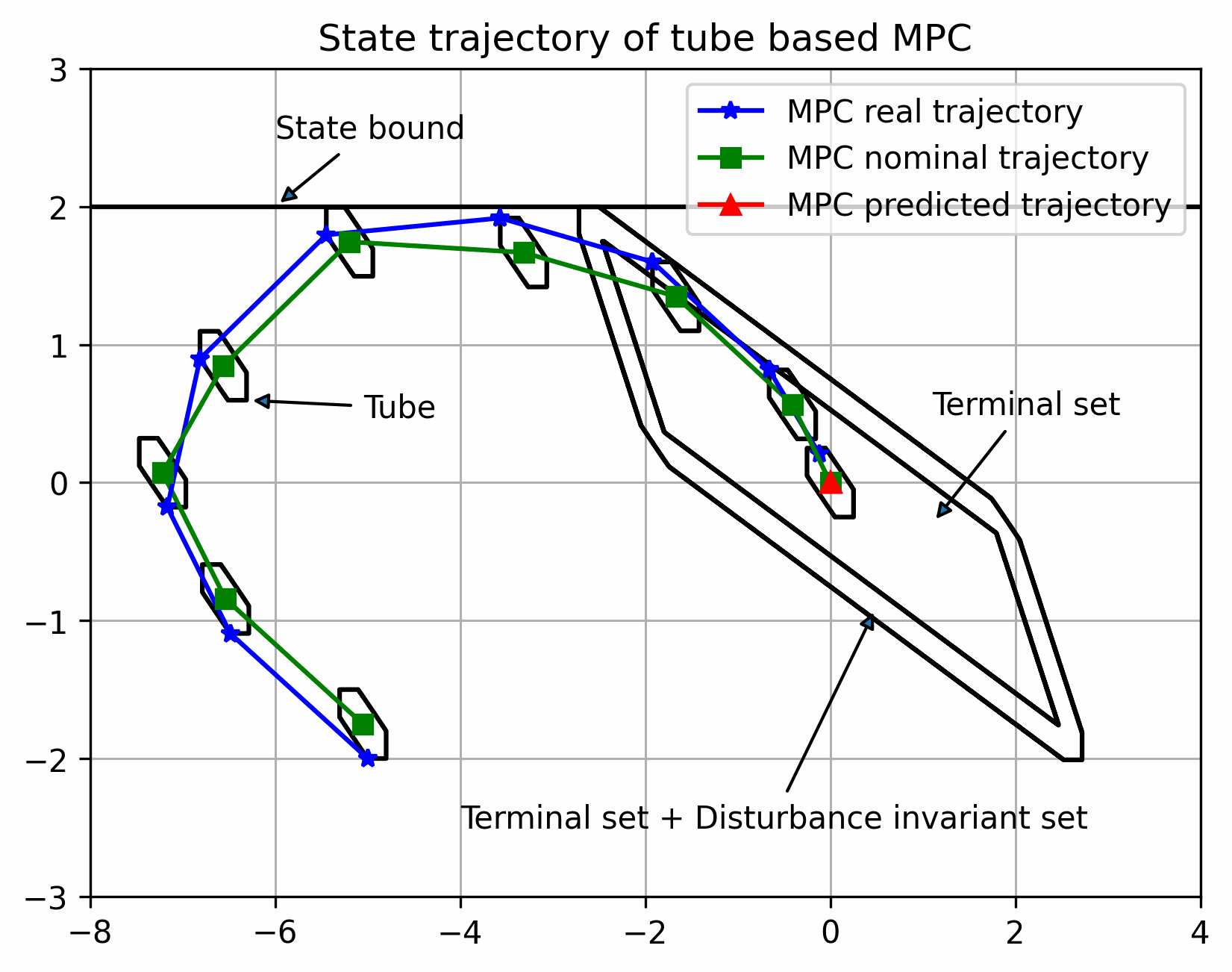
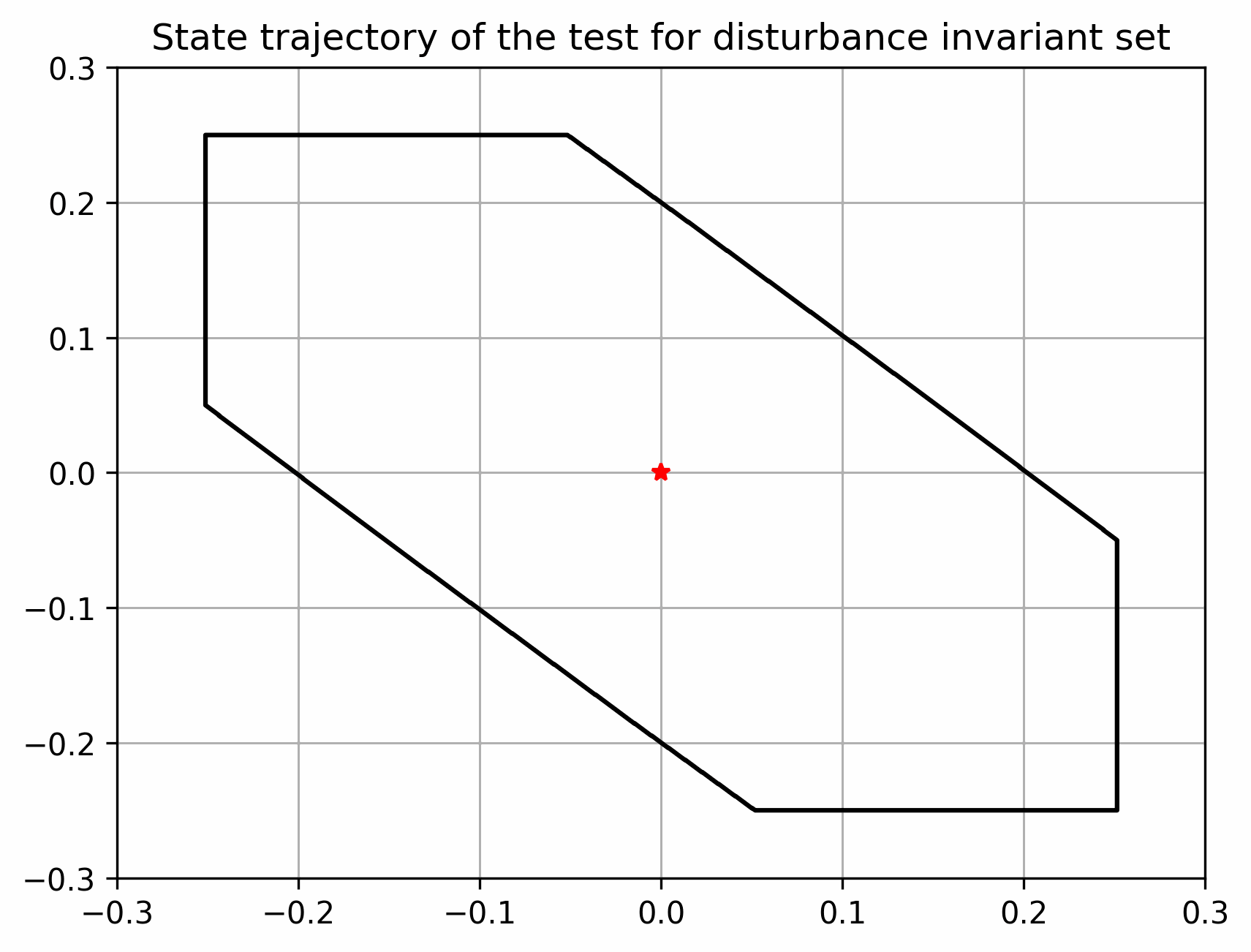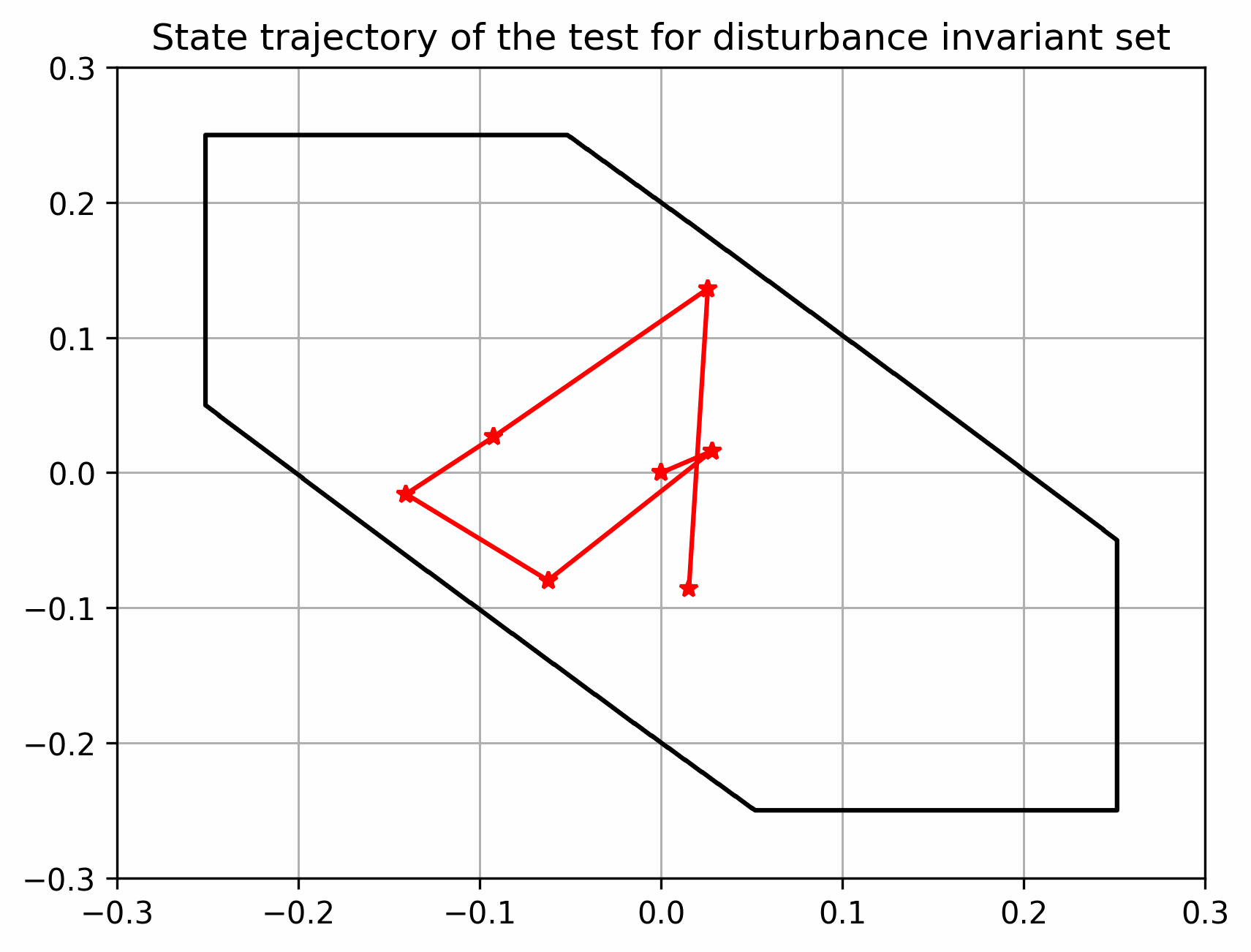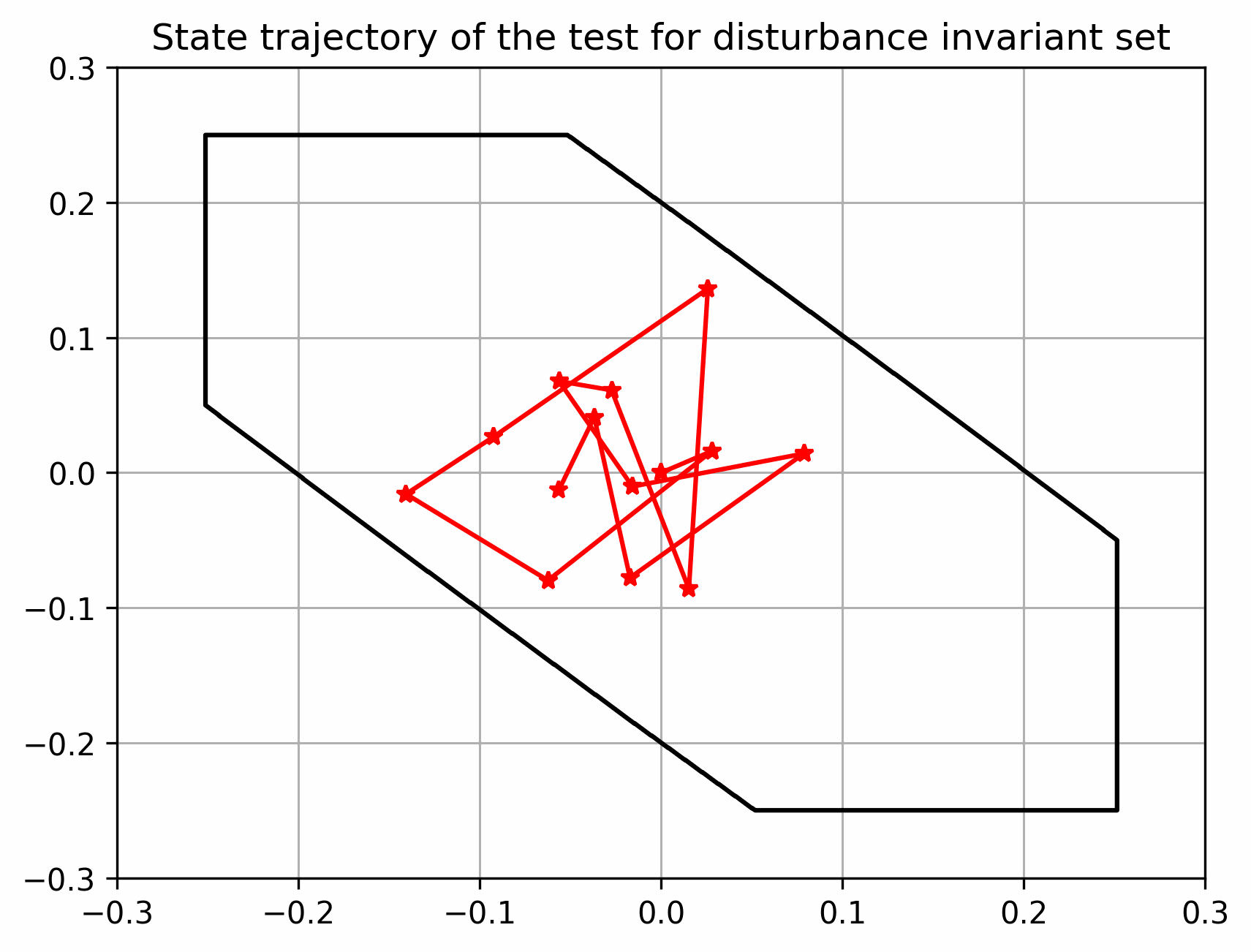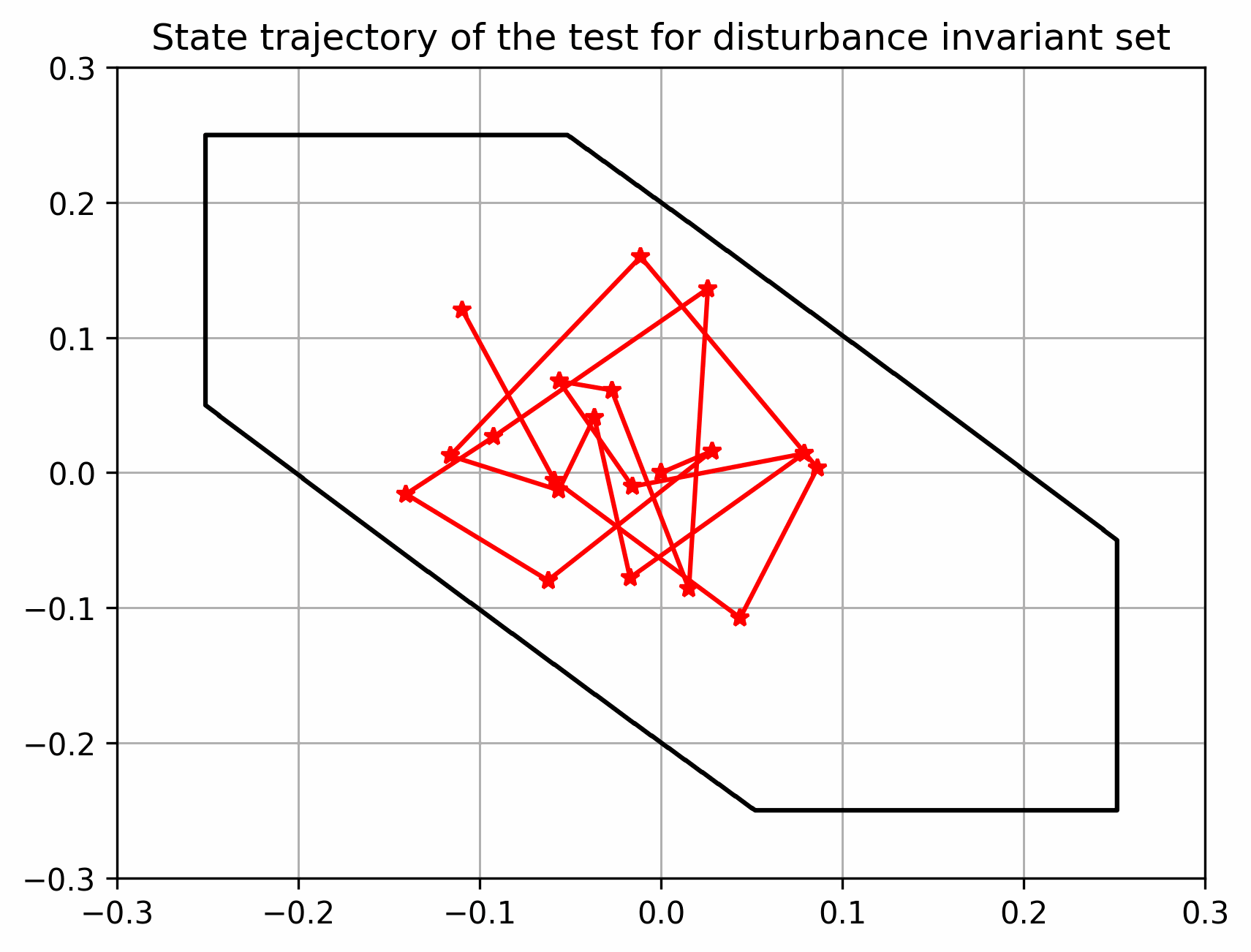
实际状态始终在以名义状态为中心的管道内
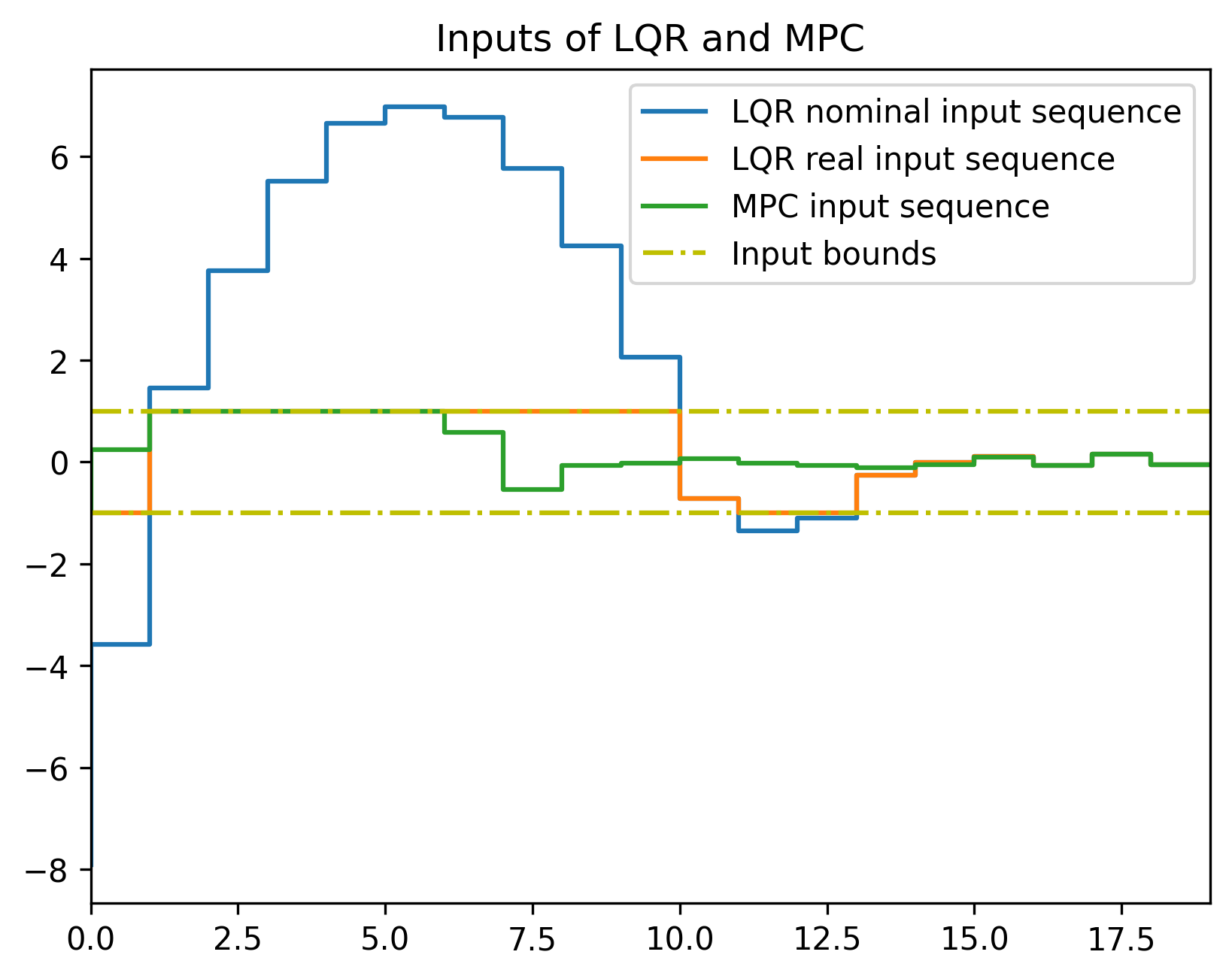
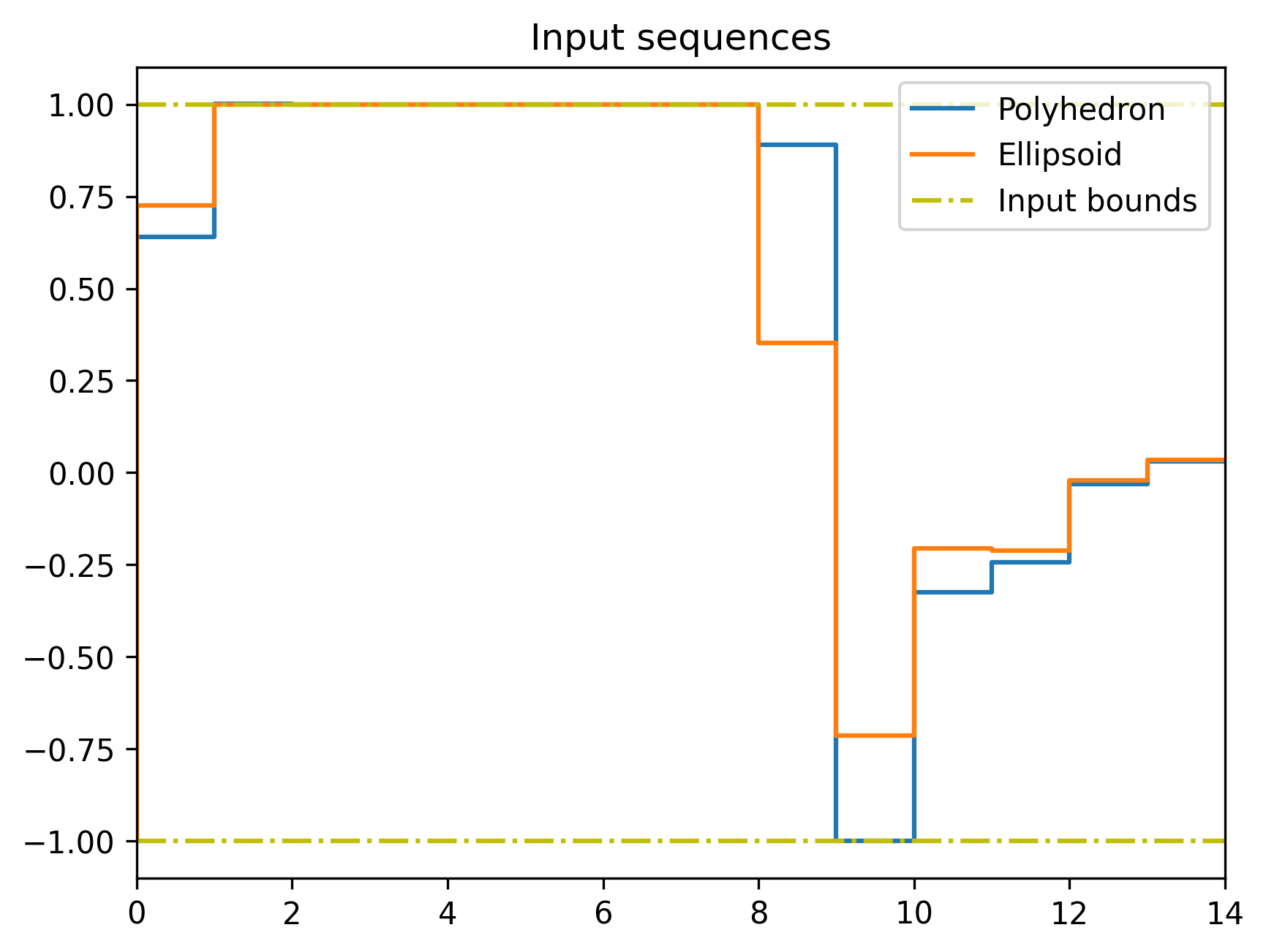
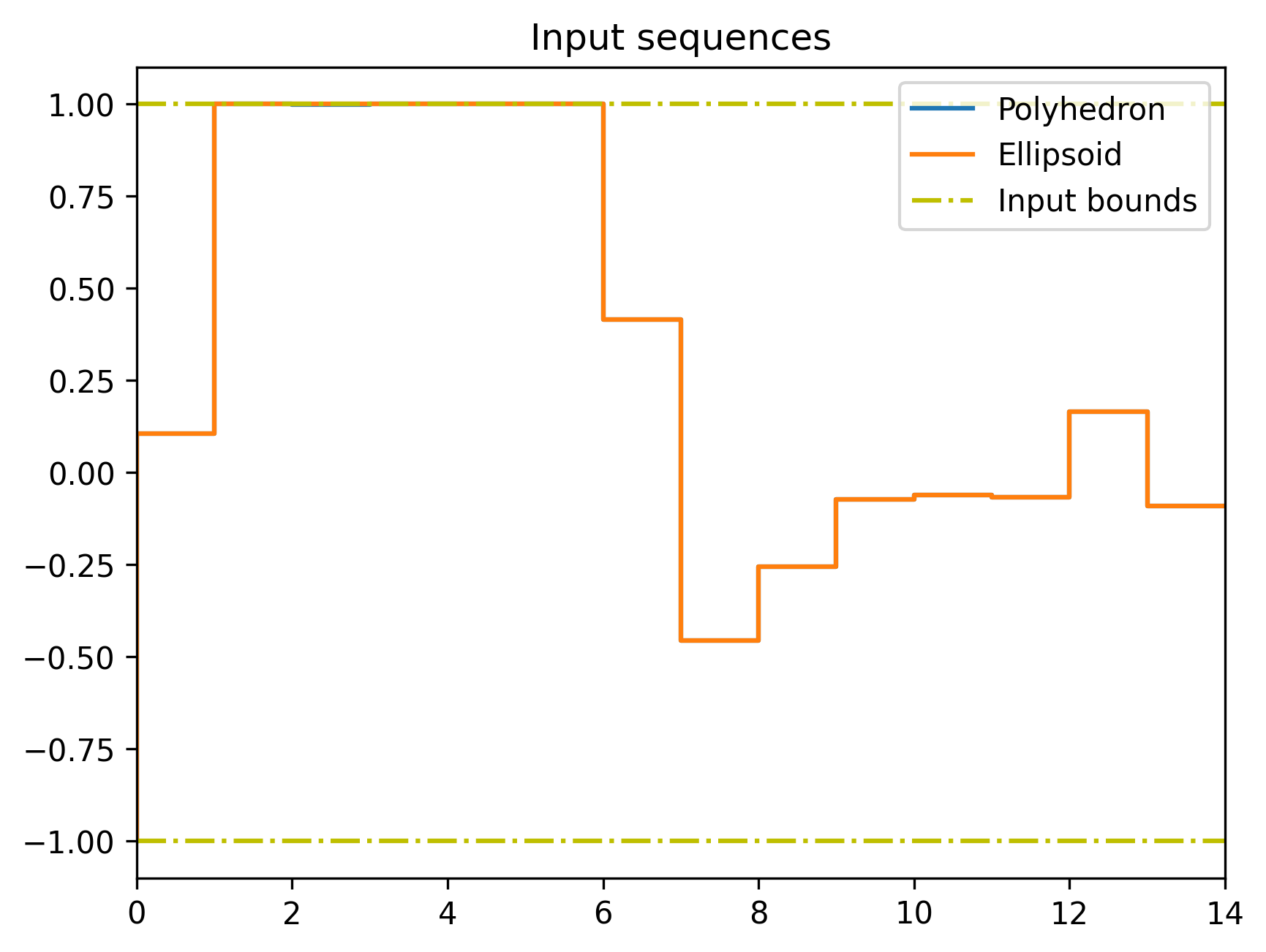
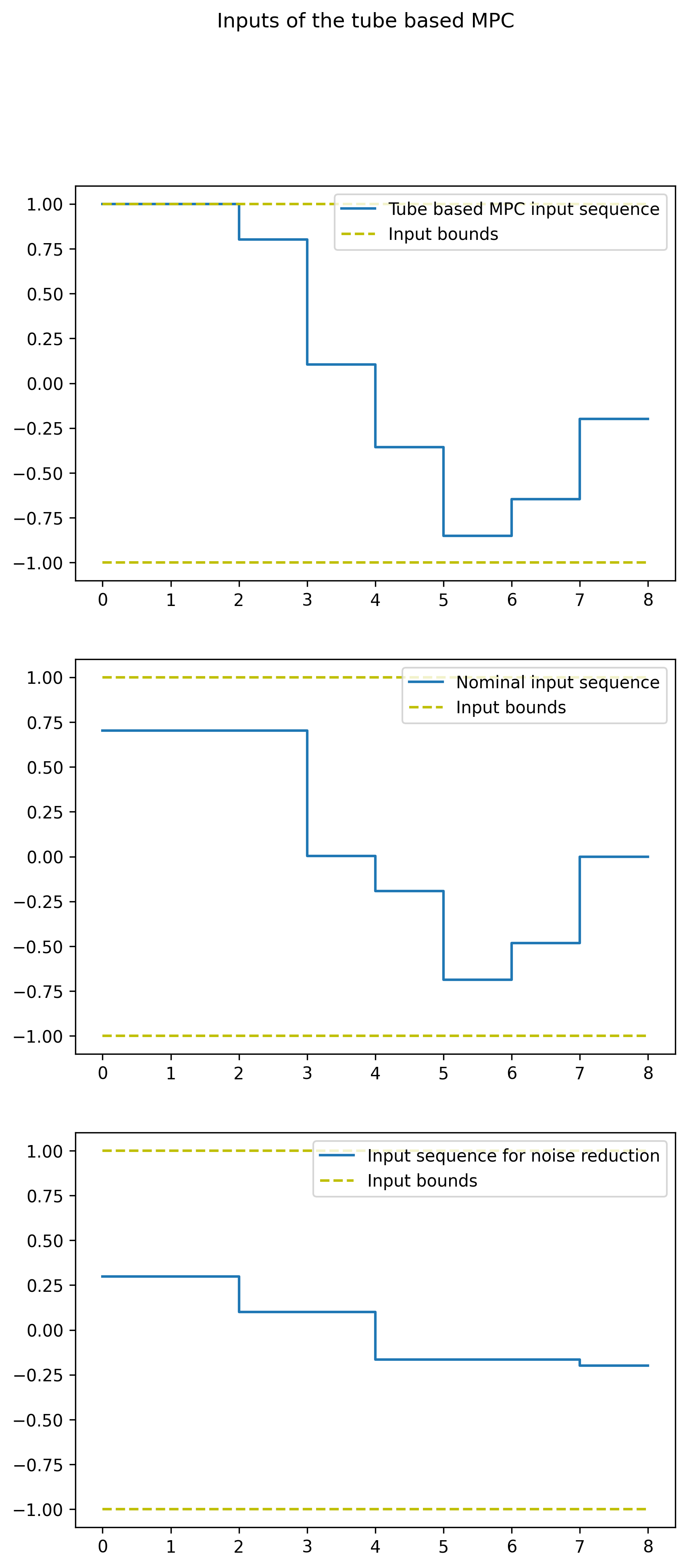
分为两部分,不考虑噪声的名义系统输入和用于抑制噪声的输入
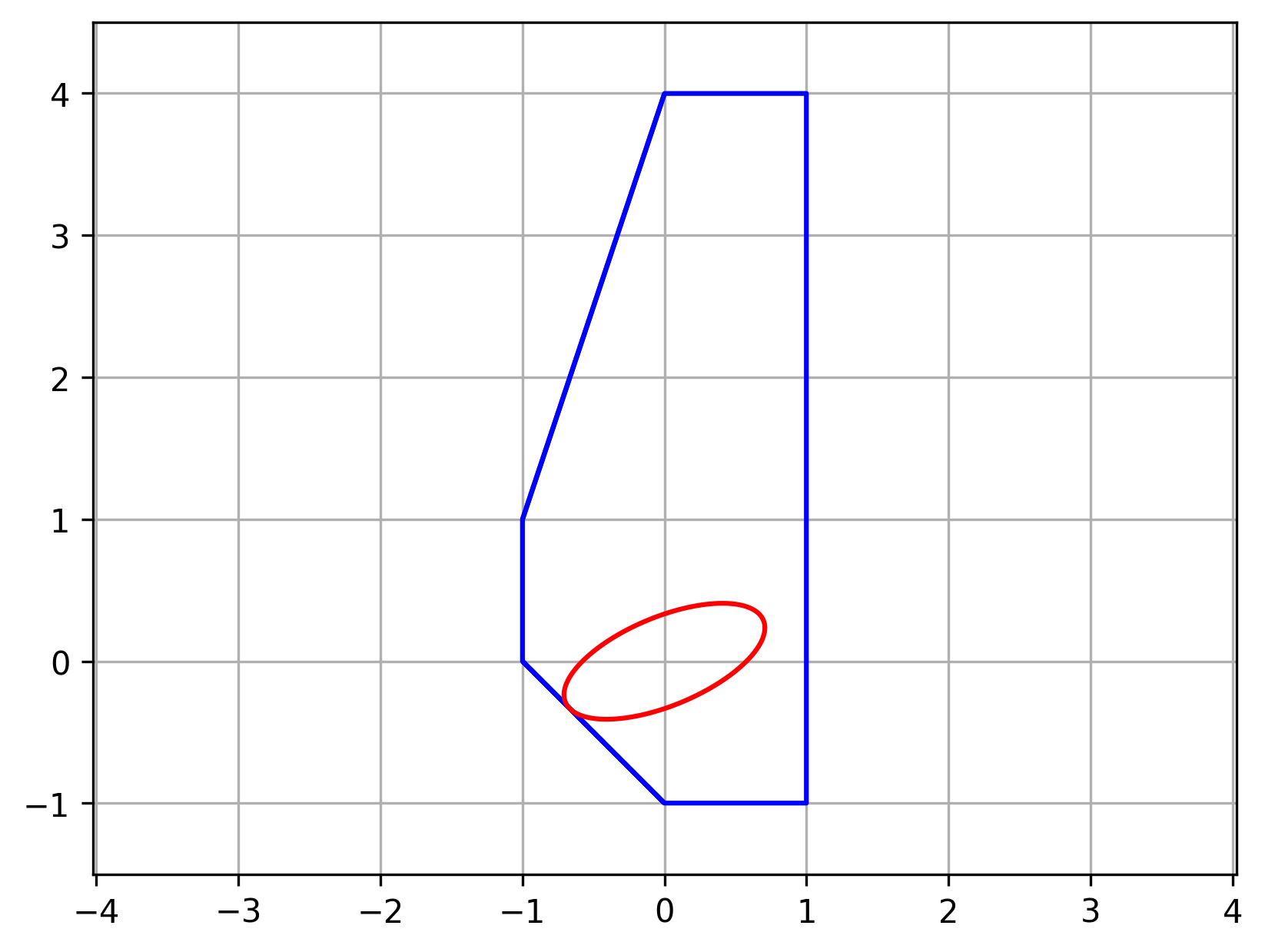
蓝色为实际可行域,红色表示控制器内预测状态序列的第一步的状态的可行域
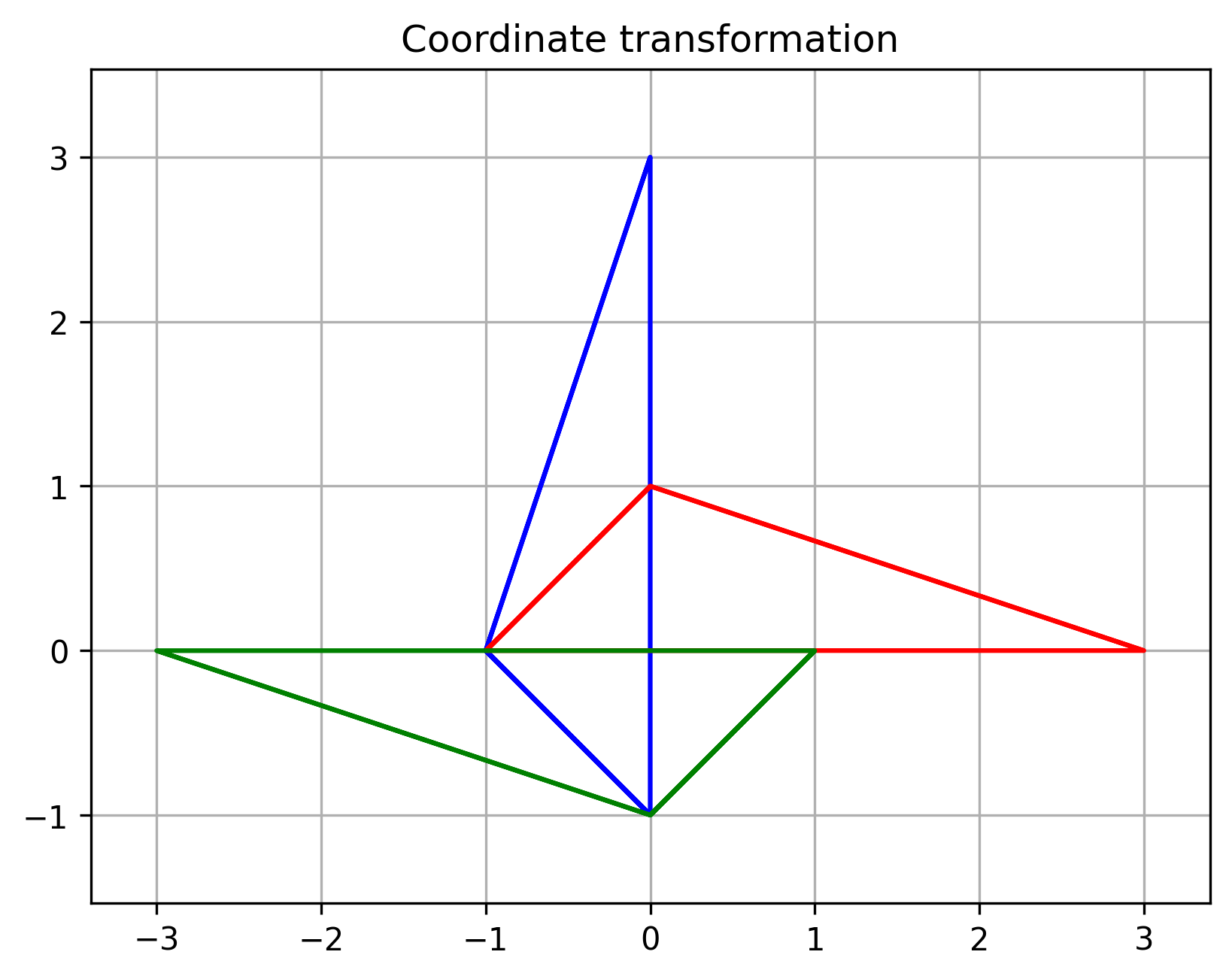
下图说明一个状态方程为