A solver for the game 'Jumble'. Given a dictionary and any word, this program returns the possible anagrams and sub-anagrams. For any clarifications, contact me (Rishabh Bhattacharya) at ribhattacharya@ucsd.edu. Happy Jumbling!
To create a conda environment, run this in the terminal (assuming you have Anaconda or Miniconda installed on your system).
conda env create -f environment.yml
This will create a conda environment named jupyter_solver on your system, installing the required packages.
NOTE: You could completely skip this step, since the solver only uses native python packages. However, this is required if you want to run tests.py and plot graphs.
To run the script, enter the following in your command line
cd ~/path/to/Jumble-Solver
python3 jumble_solver.py YOUR_DICTIONARY.txt YOUR_WORD
For example, given the (default) dictionary corncob_lowercase.txt and the (default) word dog, we would run
python3 jumble_solver.py corncob_lowercase.txt dog
Since these are default values, you could also run the same by entering
python3 jumble_solver.py
Running either of the two commands above would give, this output.
------------------------------------------------------------------------------------
Sub-anagrams found: 16
Valid sub-anagrams: 4
Valid sub anagrams are: {'do', 'dog', 'go', 'god'}
Time elapsed: 15.77 ms
------------------------------------------------------------------------------------
To run the tests and view plots, run
python3 tests.py
- environment.yml: Conda environment setup file.
- constants.py: Constant values like word file diectory.
- jumble_solver.py: Main interface script for this problem.
- tests.py: Script to perform testing and performance evaluation.
- utils/
- file_utils.py: File manipulation functions.
- test_utils.py: Contains various utility functions for testing and visualizing performance.
- utils.py: Contains various utility functions.
- scripts/
- sub_anagrams.py: Compute all possible + valid sub-anagrams.
- dictionaries/
- mit_10k.txt: MIT 10K word list (10K words)
- corncob_lowercase.txt (default): Corncob lowercase world list (58K words)
- english3.txt: English_3 (194K words)
- words_alpha.txt: words_alpha (370K words)
- Checks if dictionary file exists and if input word contains alphabets, else raises error.
- Dictionary is implemented as a hashset, so sorting is not needed and duplicate elements are rejected inherently.
- Handles upper/lower case and combinations by converting the dictionary and input word to lowercase for uniformity across permutations and search.
- The sub-anagrams are also stored as hashsets. Thus even if input word has duplicate alphabets, the sub-anagrams are unique.
- Search takes
$O(1)$ complexity on average due to thesetinplementation.
The algorithm is as follows:
- Check if the dictionary exists and the input words is valid.
- Read the dictionary and store it as a set.
- Permute the sub-anagrams and check if it exists in the dictionary. If yes, store it in another set.
- Return the set of all valid sub-anagrams.
I used Python's hashset set() for this implementation. Insertion in both set() and List[] take set()) improves upon the previous build (using List[] and binary search) majorly due to two factors,
- Search in a
set()takes$O(1)$ time, and it is not required to be sorted. In contrast, binary-search in a sortedList[]takes$O(\log m)$ time, and the sorting (if dictionary is unsorted) itself takes$O(m\log m)$ time. Both end up taking the same space$O(m)$ . - If the input word has repeated characters, there would be duplicate permutations when adding in a
List[]. Rather than trying to remove duplicates separately, adding elements in aset()ensures that no duplicates are added. Both methods take$O(1)$ time to append each element, but we achieve duplicate removal as a bonus by usingset().
If dictionary has
-
Reading dictionary: Time:
$O(m)$ , Space:$O(m)$ - Traversal over dictionary.txt file:
$O(m)$ - Adding to set:
$O(1)$ for each element in dictionary -
Total time:
$O(m)$ -
Total space:
$O(m)$
- Traversal over dictionary.txt file:
-
Computing all possible sub-anagrams:Time:
$O(\lfloor n! \times e\rfloor)$ , Space:$0$ - Permuting r letters at a time:
$O({}^n P_r)$ - Adding to set:
$O(1)$ for each element -
Total time:
$O({}^n P_n + {}^n P_{n-1} + \cdots {}^n P_1 + {}^n P_0) = O(\sum_{r=0}^n {}^n P_r) = O(\lfloor n! \times e\rfloor)$ . See this link for the derivation. -
Total space:
$0$ , sincepermutationsfromitertoolsusesyieldto return values, so the values are not stored at the same time. Also we are only storing the words that have been found in the dictionary. This happens in the search step.
- Permuting r letters at a time:
-
Search for valid sub-anagrams: Time:
$O(1)$ , Space:$O(k)$ where$k$ is the number of valid matches in the dictionary.- Search for a sub-anagram in set of words (dictionary):
$O(1)$ -
Total time:
$O(1)$ -
Total space:
$O(k)$
- Search for a sub-anagram in set of words (dictionary):
Thus given
| Step # | Step description | Time complexity | Space complexity |
|---|---|---|---|
| 1 | Reading dictionary | ||
| 2 | Computing all possible sub-anagrams | ||
| 3 | Search for valid sub-anagrams | ||
| Total |
The total time complexity has a peculiarity, where the dominant term can either be the length of the dictionary
The complexities are thus given by
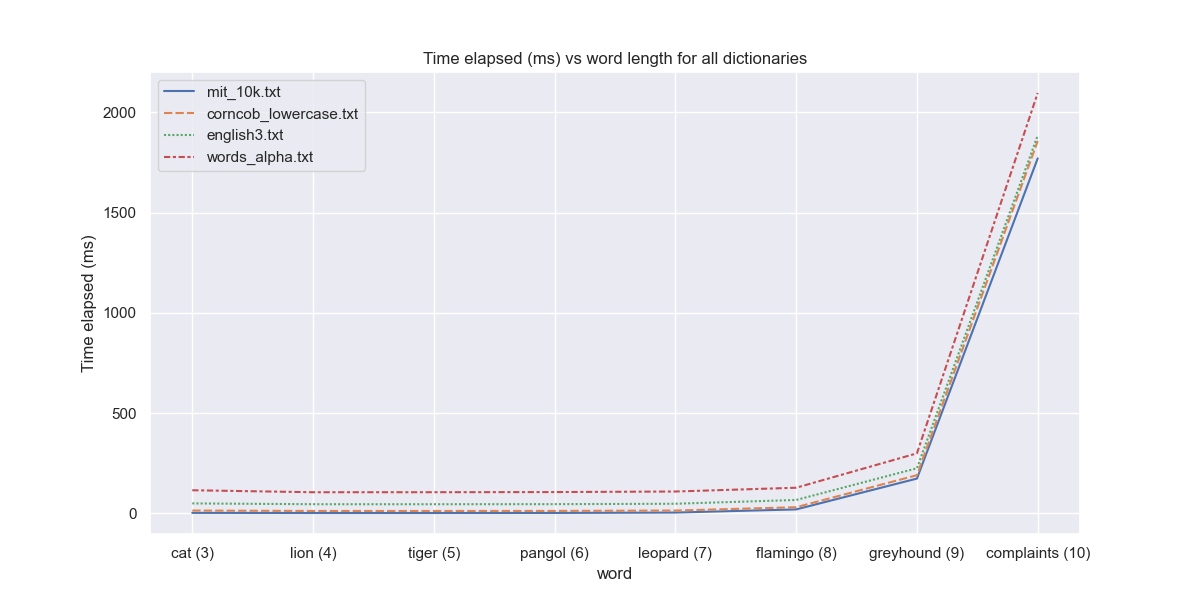
I chose the following dictionaries and words to compare and evaluate a comprehensive performance overview.
dictionaryNames = ['mit_10k.txt', 'corncob_lowercase.txt', 'english3.txt', 'words_alpha.txt']
words = ['cat', 'lion', 'tiger', 'pangol', 'leopard', 'flamingo', 'greyhound', 'complaints'] # There's very few 10 letter animals :-(
It is clear from the graph above that permutations of longer words are more time consuming. We also see an increasing trend of time with the size of dictionary. Note that
- the runtime for
$n \leq 7$ (cat to pangol) is similar for a given dictionary, and does not change much with$n$ (word length). This region is where$O(m)$ dominates, and thus the runtime looks uniform for a given dictionary, regardless of the input word length$n$ . -
$n={7,8}$ is where no clear dominating effect emerges, and is based on which dictionary has been chosen. This is kind of the transition region. - However, we start seeing a sharp increase at
$n=9$ . This is where$O(\lfloor n! \times e\rfloor) >> O(m)$ , and the sub-anagram computation dominates the reading of all dictionaries.
I attempt to support this claim by the following.
| Dictionary | # of words ( |
|---|---|
mit_10k.txt |
10,000 |
corncob_lowercase.txt |
58,000 |
english3.txt |
194,000 |
words_alpha.txt |
370,000 |
| Word length |
|
Compared to |
|---|---|---|
| 1 | 2 | Computation time for sub-anagrams < reading all dictionaries |
| 2 | 5 | Computation time for sub-anagrams < reading all dictionaries |
| 3 | 16 | Computation time for sub-anagrams < reading all dictionaries |
| 4 | 65 | Computation time for sub-anagrams < reading all dictionaries |
| 5 | 326 | Computation time for sub-anagrams < reading all dictionaries |
| 6 | 1957 | Computation time for sub-anagrams < reading all dictionaries |
| 7 | 13700 | Computation time for sub-anagrams > reading mit_10k.txt (10K words). Other dictionaries are still the bottleneck. |
| 8 | 109601 | Computation time for sub-anagrams > reading mit_10k.txt (10K) and corncob_lowercase.txt (58K). Other dictionaries are still the bottleneck. |
| 9 | 986410 | Computation time for sub-anagrams > reading all dictionaries. From |
Thus we see that for the given 4 dictionaries,
- For
$n \leq 6$ , the dictionary read/write is the bottleneck. - For
$n={7,8}$ , the bottleneck depends on which dictionary has been chosen. - For
$n \geq 9$ sub-anagram computation is always the bottleneck.
This analysis lets us focus on which process to prioritize and optimize. I believe that most words that we play with will be less than 9 characters in length. This means that we would benefit a lot by optimizing the dictionary read/write process into the working memory.
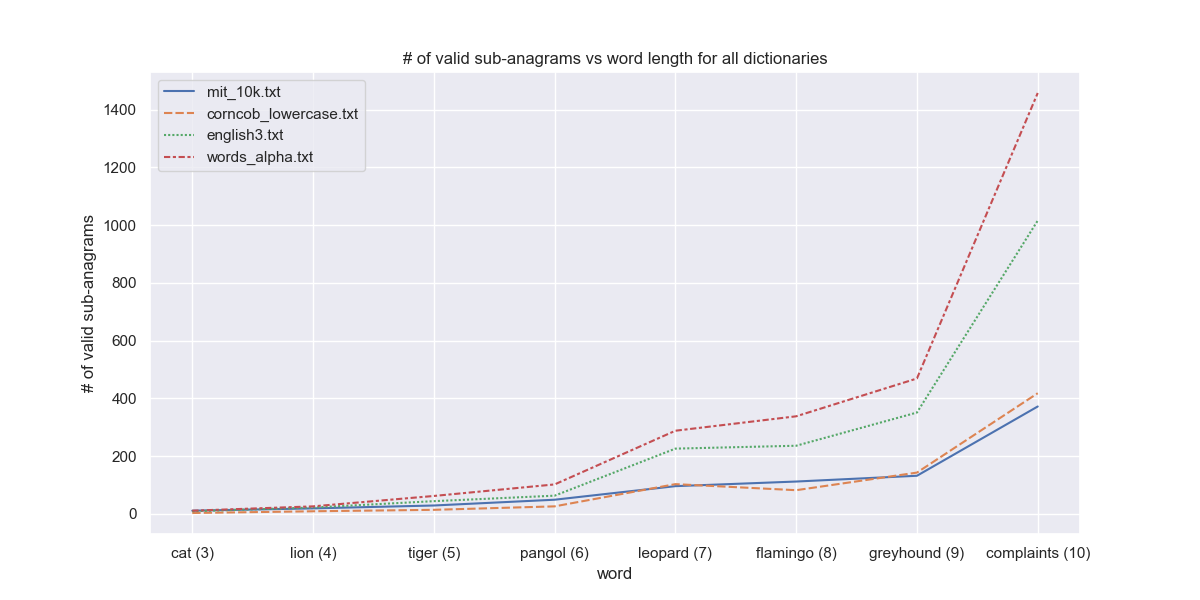
We also see a dramatic increase of the number of valid sub-anagrams with word length. There is one anomaly, i.e. for mit_10k and corncob_lowercase. We would expect the former to result in less valid sub_anagrams, since it has lesser words (10K vs 58K). However, this does not happen because the mit_10k dictionary contains many nonsensical words, as evidenced by the following.
$ python3 jumble_solver.py mit_10k.txt dog
------------------------------------------------------------------------------------
# of all possible sub-anagrams: 16
# of valid sub-anagrams: 10
Valid sub-anagrams are: {'go', 'o', 'g', 'god', 'do', 'dg', 'og', 'd', 'dog', 'gd'}
Time elapsed: 2.77 ms
------------------------------------------------------------------------------------
We can see that {'o', 'g', 'dg', 'og', 'gd'} are not actual words, and are hence not found in the corncob_lowercase dictionary, but are present in the mit_10k dictionary. This leads to many extraneous sub-anagrams. This problem only gets worse for longer words.
- If we have repeating characters in the input word, the duplicate permutations are currently computed before attempting to add into the
set(). A further optimization could be to skip this computation itself. - We could read the input word and only load corresponding sections from the dictionary. Eg, for input 'dog', we can only load words that start with 'd', 'o' or 'g'. This would reduce the space complexity manyfold, but introduce multiple checks for each word in the dictionary (
$O(3m)$ in this case:$m$ words being checked thrice against 'd', 'o' and 'g'). In order to rectify that, we could pre-process the dictionaries and split them into 26 dictionaries, based on their starting letter. Thus, for the input 'dog', we can load only the 'd', 'o' and 'g' dictionaries, which would be both computationally and memory favourable.