Genetic Algorithm for Path Planning

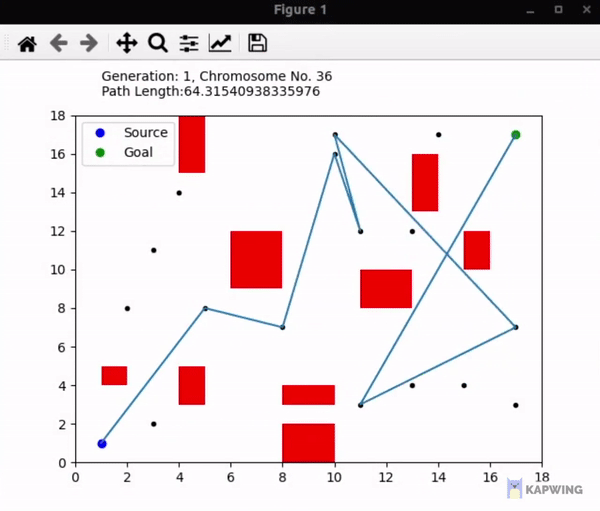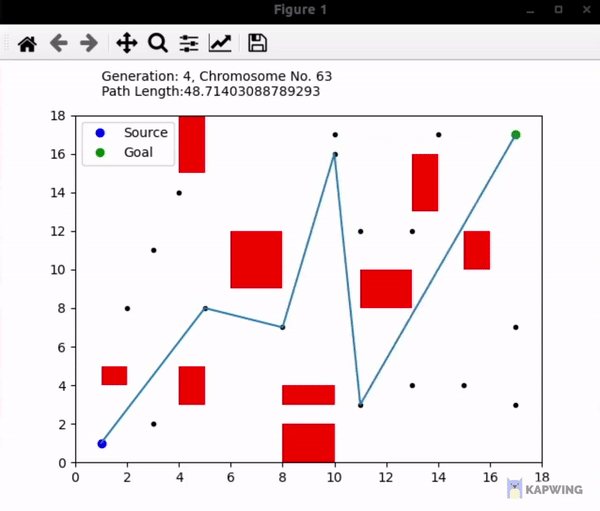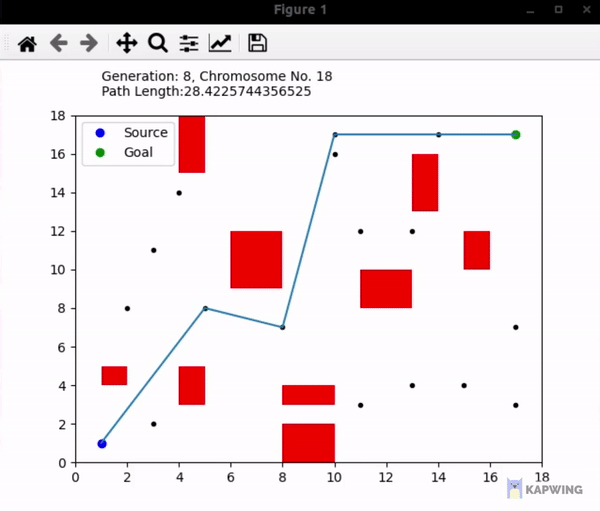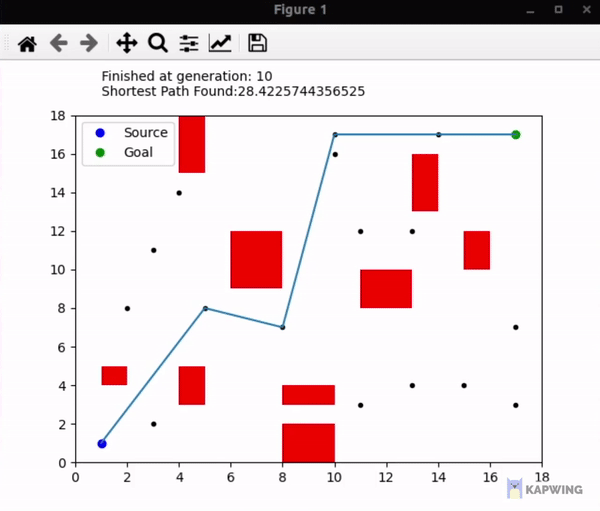
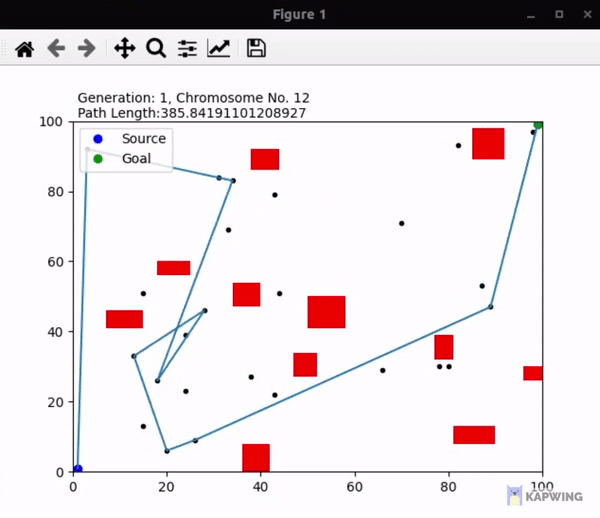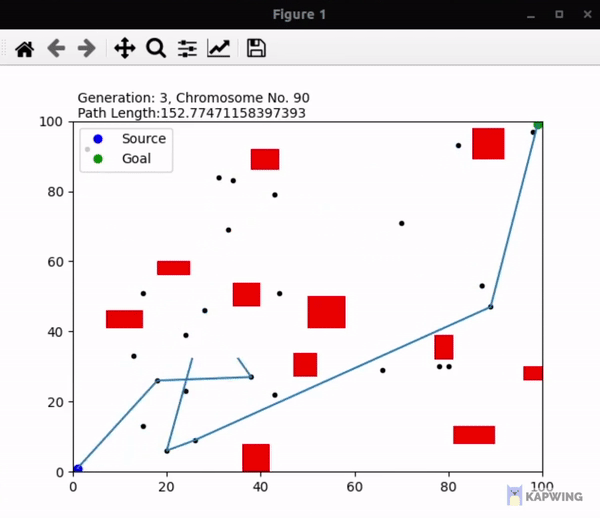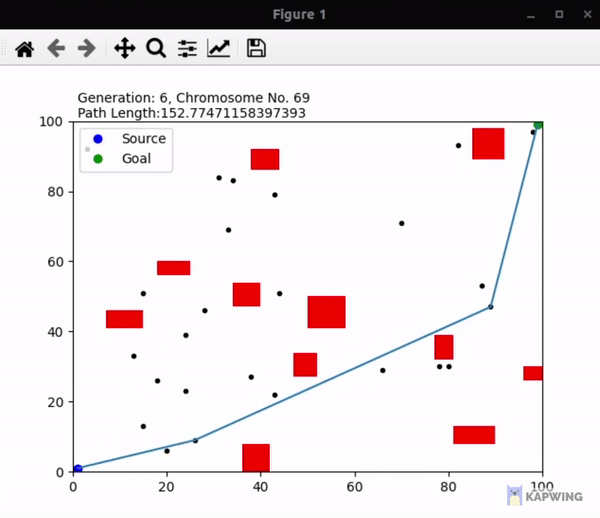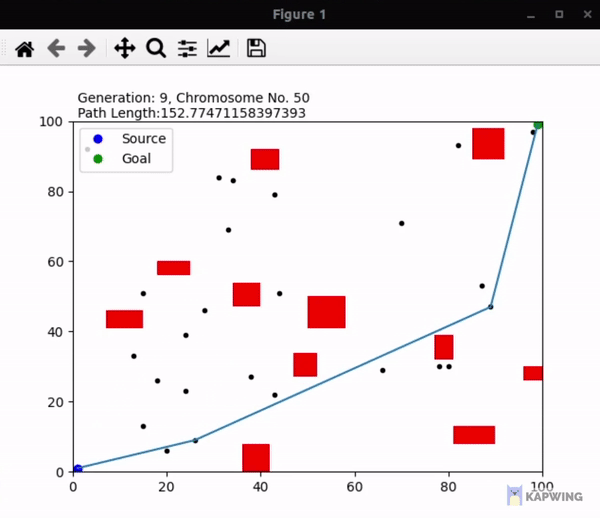
An implementation of the genetic algorithm used in finding the shortest path from one point to another with some obstacles in between using the path points available throughout the space. I've used Matplotlib to show the simulation. Some help was taken from Yaaximus' implementation here, but the approach taken is different and I've coded ways to generate obstacles and path points randomly so the method is a lot more dynamic rather than focusing on static obstacles and paths.

Setup Instructions

Make sure you have Python 3.6 or above installed. Clone the repo, and do the following in the directory.

Linux

python3 -m venv env
source env/bin/activate
pip install -r requirements.txt
python3 simulate.py

Windows

python -m venv env
env\Scripts\activate.bat
pip install -r requirements.txt
python simulate.py

You can change the setup variables in config/config.ini as you wish, although combinations of some values can produce impossible paths or take a very very long time e.g very large population size, huge number of obstacles for the axes, lots of path points, very small axis size etc.

There are hardcoded obstacles and path points available too for comparison purposes from Yaaximus' implementation, which are used automatically if generated_randomly in the config.ini is set to false.

Simulation

Details

Chromosomes are binary coded and generated randomly, each bit representing whether that path point is visited or not. First and last bit are always 1, because source and goal are always visited.
The source is always generated at the bottom left, and goal on the top right.
Path points are never generated very close to any obstacle, and obstacles also never overlap.
For the fitness function, I've used the simple reciprocal of the total distance covered by the path.
To mutate, I choose any random bit from the chromosome and flip it. Source and goal bits are ignored.
Crossover is done by splitting parent chromosomes in two and joining with each other. Split size can be configured by user or done randomly.
Unlike Yaaximus' method, no probability or links are made between close path points that could increase a path's fitness as a more dynamic approach is tried here. If we test using the hardcoded obstacles and path points, we can see the proposed solution finds a shorter path by skipping one path point.

Improvements

Some improvements can possibly be made to the simulation that could boost the performance. First, when connections between path points are being validated, we can just check against nearby obstacles instead of going over every obstacle on the map and avoid ones farther away.

Secondly, despite some optimizations, there are still instances where a very difficult map is randomly generated. For example, an obstacle being generated right in front of the source, leaving no way out from the starting node. In such cases, solutions are impossible to find and the simulation gets stuck in a loop trying to come up with chromosomes to solve it. Edge cases like these can be handled to improve the program

Instead of randomly generating obstacles all around, it could be better to create them equally distributed throughout the space still at random. It's seen that sometimes most obstacles lie leaning towards the edge or leaving gaps around the map, making path finding easy. So an equal distribution at the center and at the edges could yield better results.

Conclusion