The Poisson Equation, and its special case, the Laplace Equation, are important partial differential equations within electrostatics, as they describe the electric potential field caused by a particular charge distribution. Solving the Poisson equation for a given set of boundary conditions is a fundamental problem within the field. This report describes an algorithm for a Monte Carlo Method solution to the Poisson and Laplace equations. Monte Carlo Method is a parallelizable non- deterministic numerical approach towards solving this problem. A Python implementation is also provided for three versions of the Monte Carlo Method: Fixed Step, Semi-Floating and Full Floating. Several examples including the one-dimensional and two-dimensional parallel plate capacitors are performed to illustrate the function of the implementation.
Keywords: Poisson Equation, Laplace Equation, Monte Carlo Methods, Electrostatics, Parallel Plate Capacitor, Python Implementation
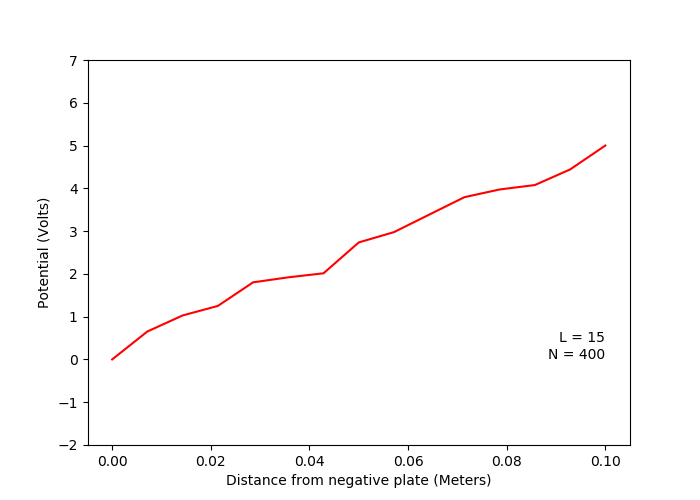
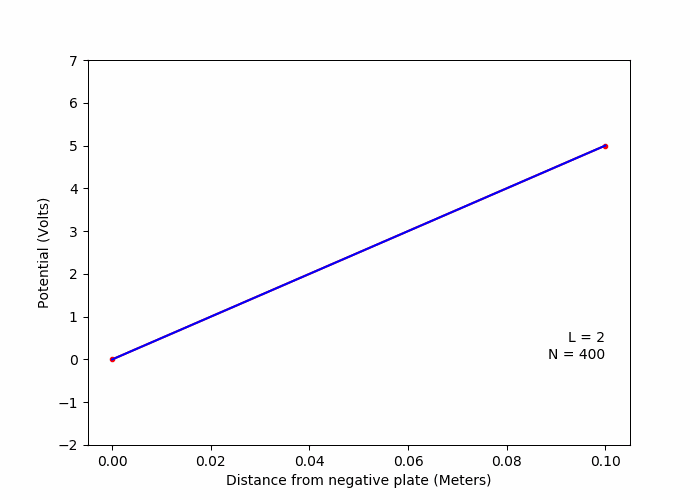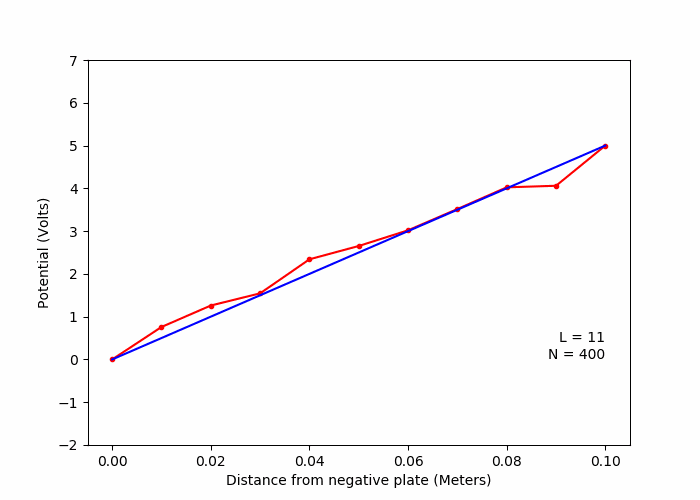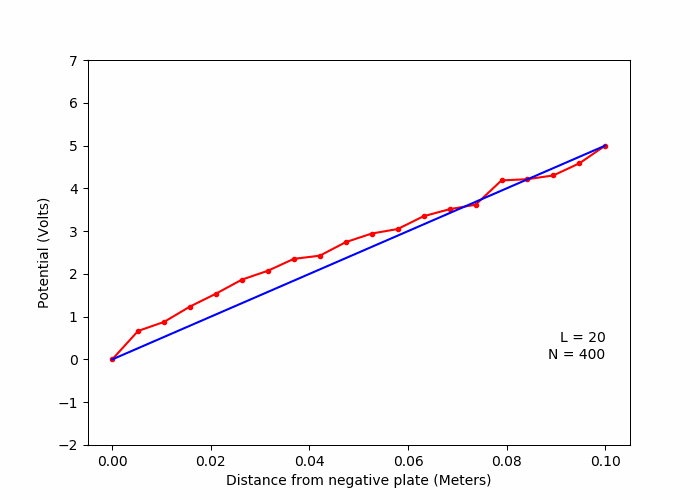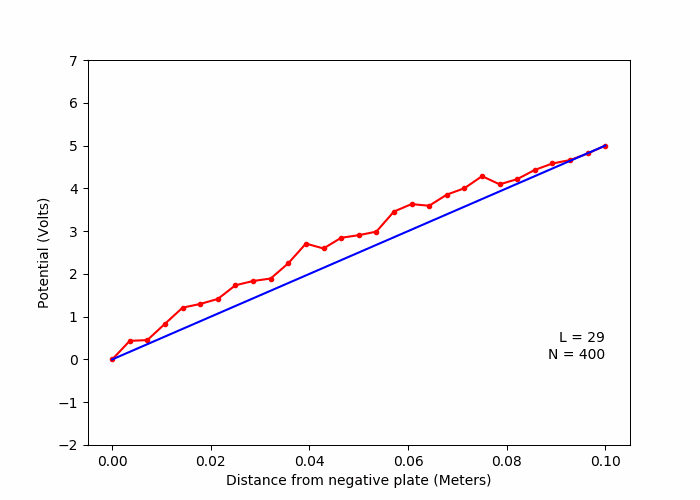
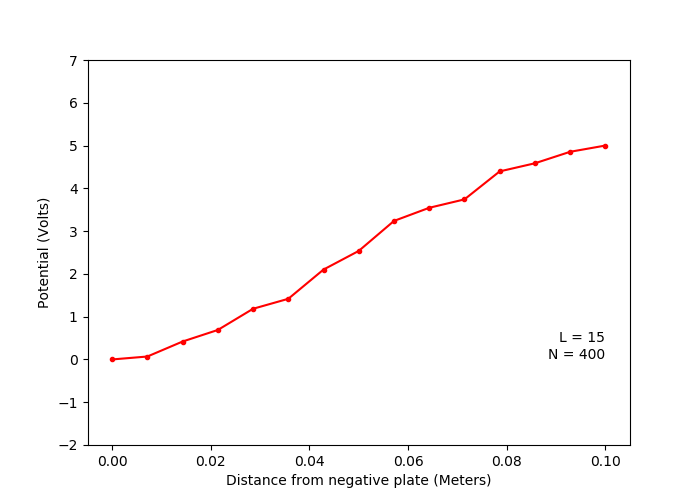
A. One dimentional capacitor (Laplace Equation)
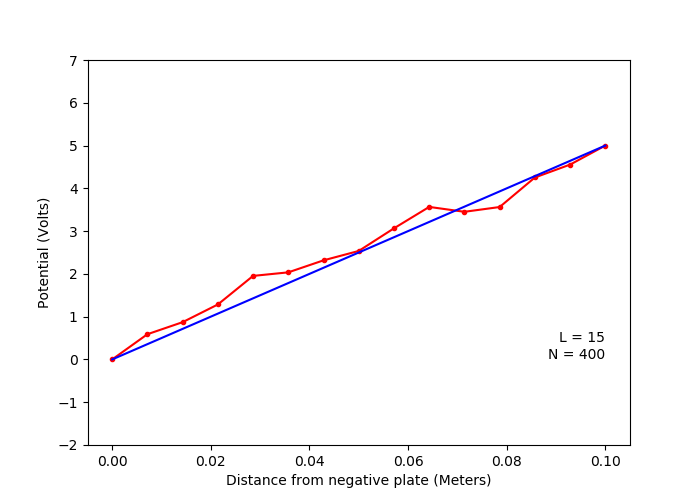
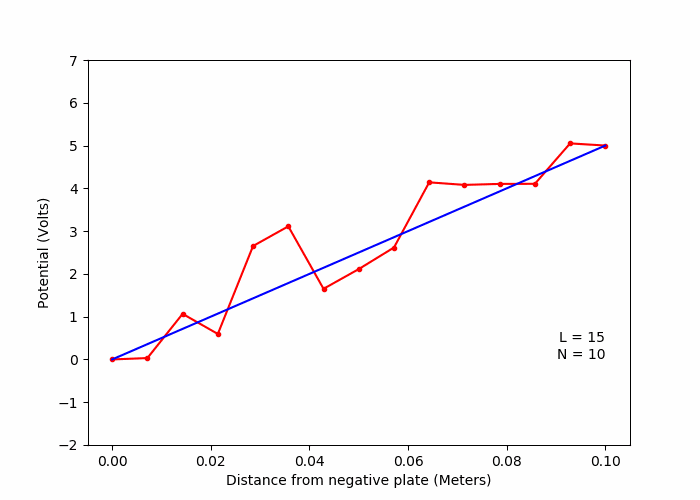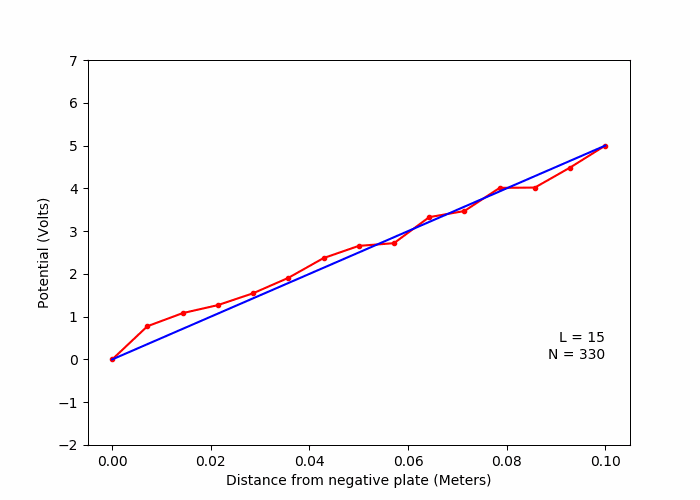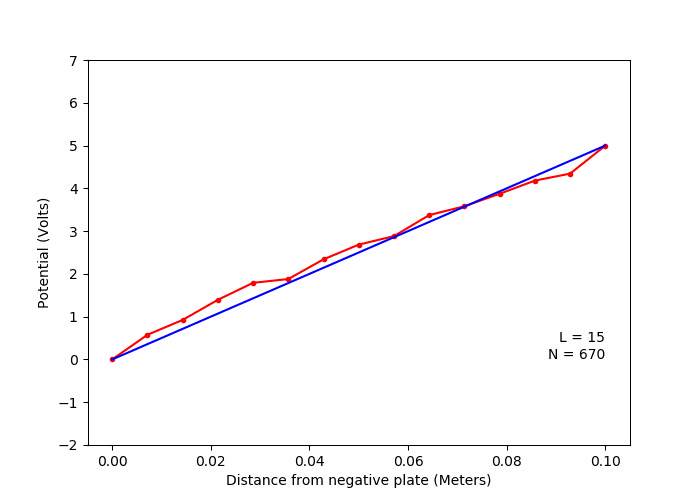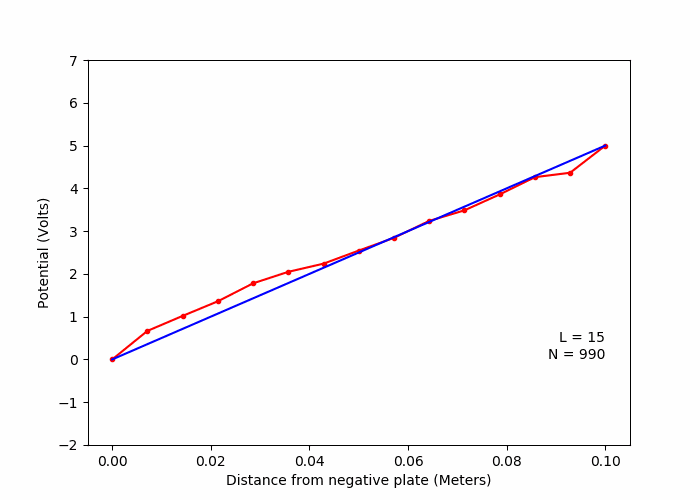
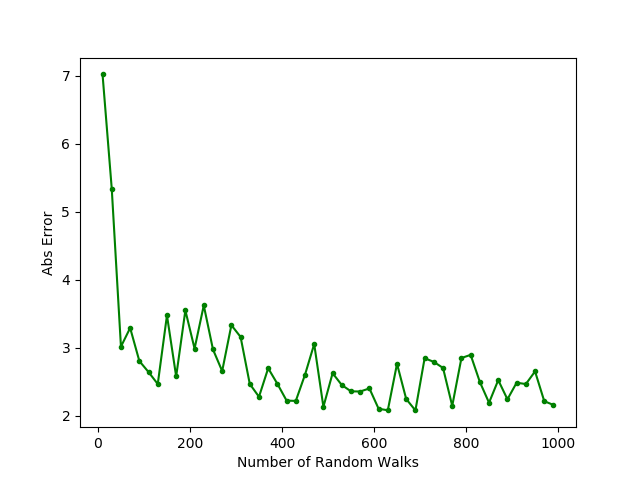
B. Variation of solution with number of random walks (Laplace Equation)
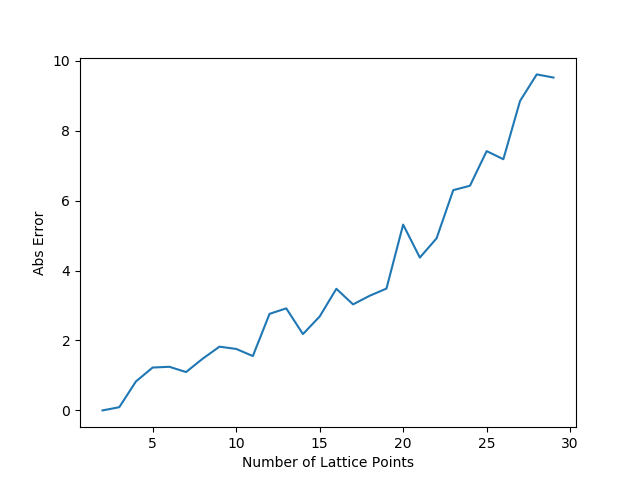
C. Variation of solution with number of lattice points (Laplace Equation)
D.One dimensional capacitor with a linear charge distribution (Poisson Equation)
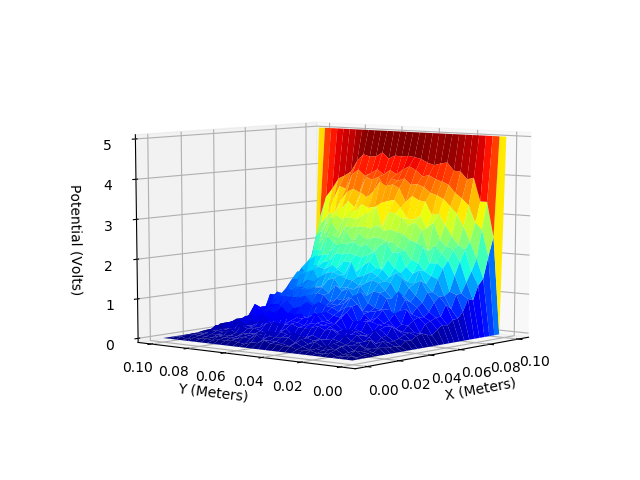
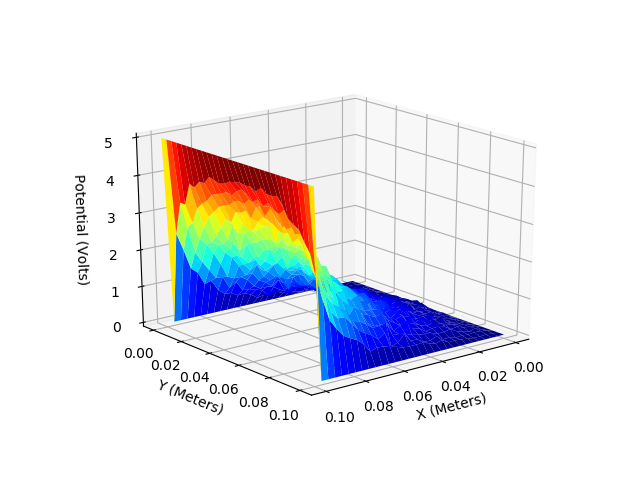
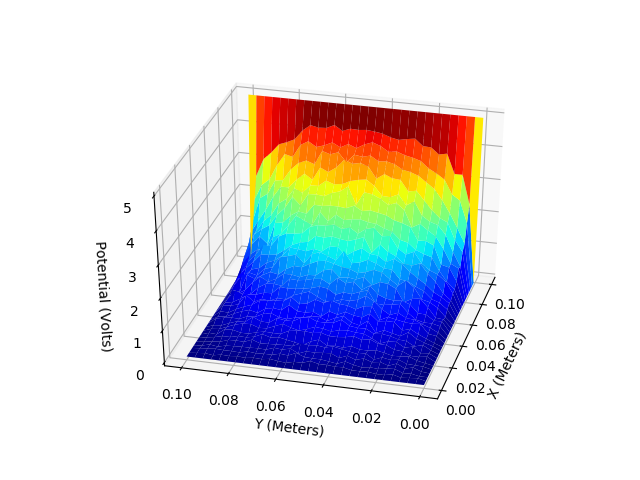
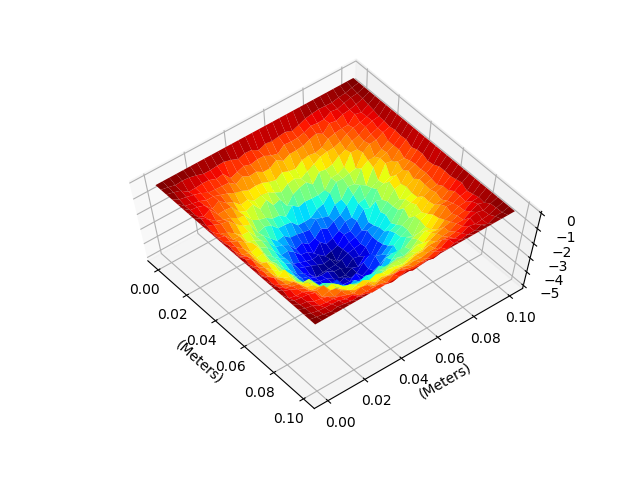
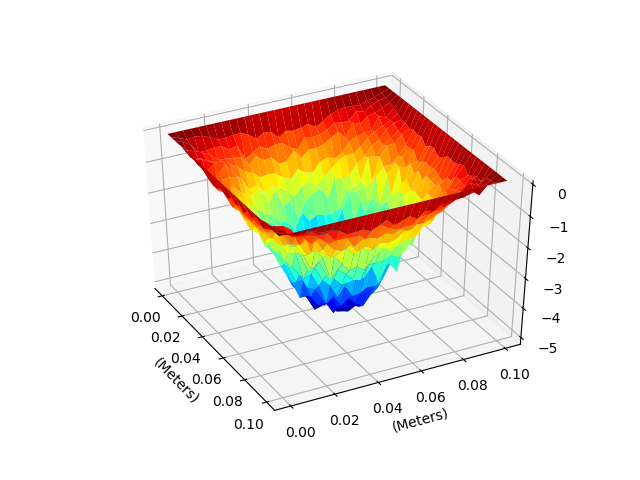
E. Two dimentional capacitor (Laplace Equation)
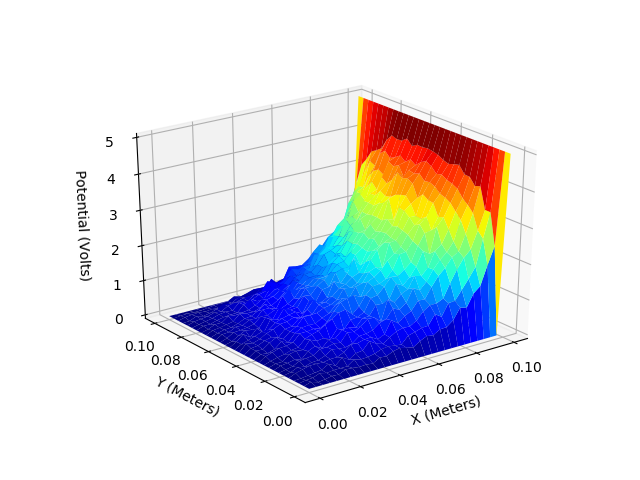
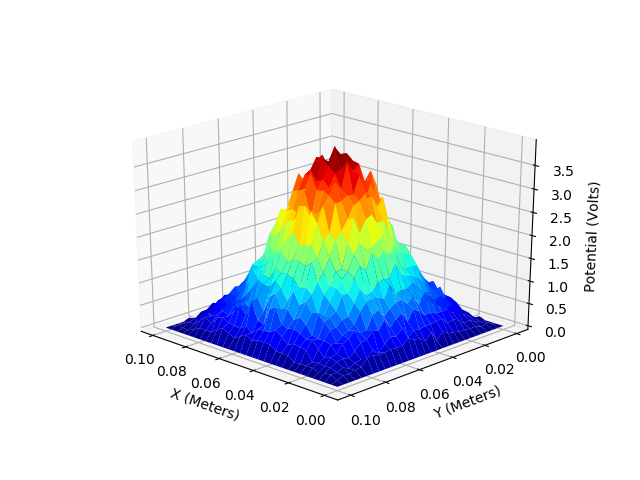
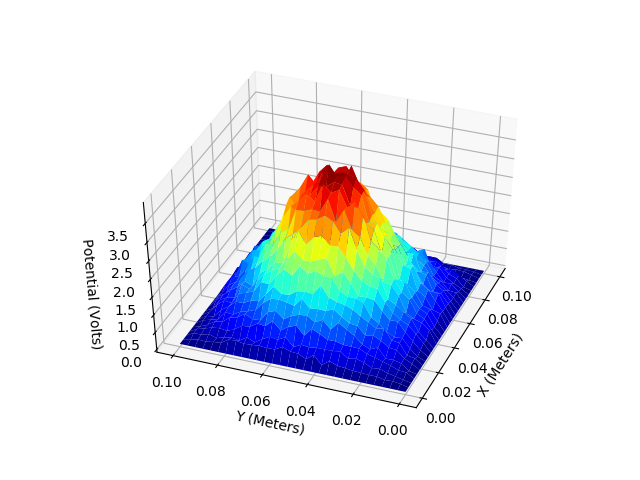
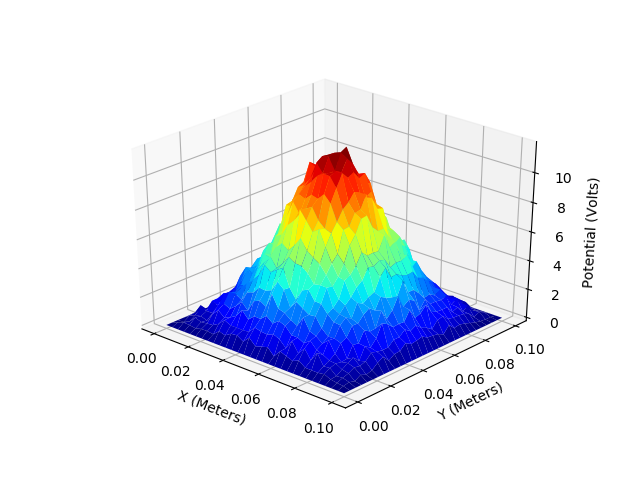
F.Two dimentional metal box with a spherical charge in centre (Poisson Equation)
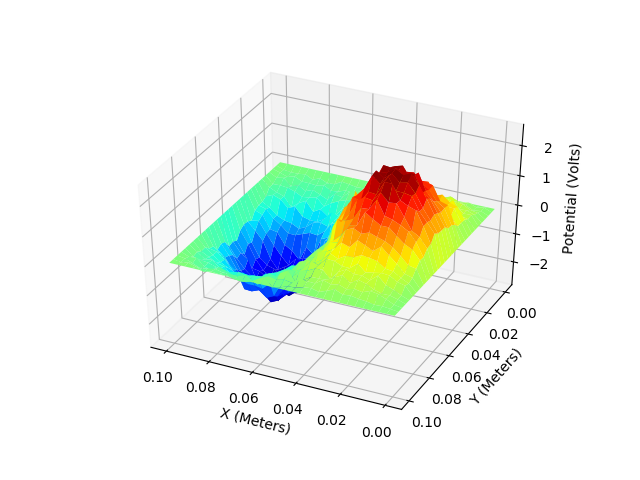
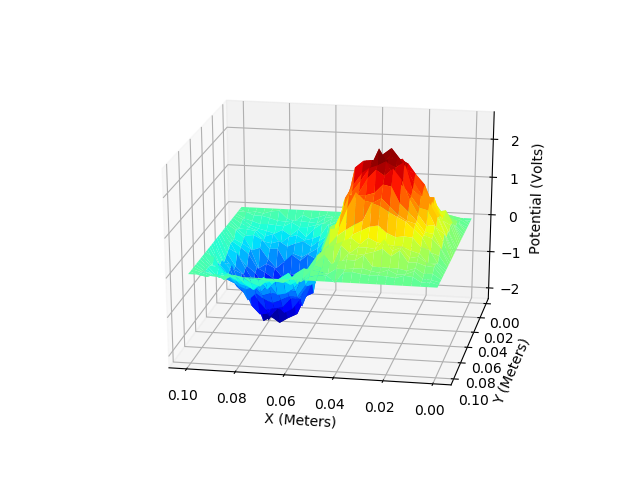
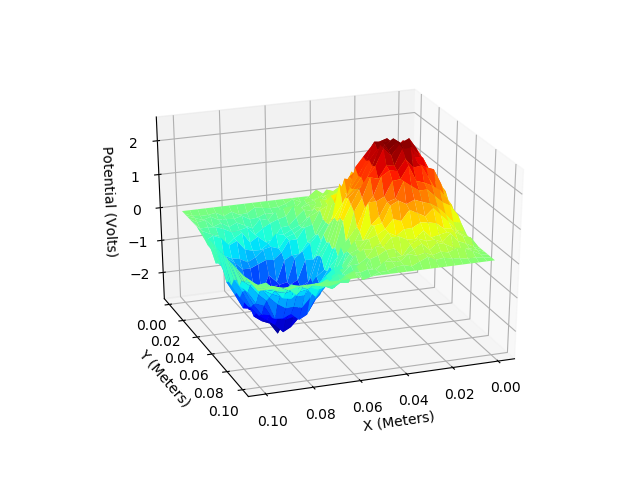
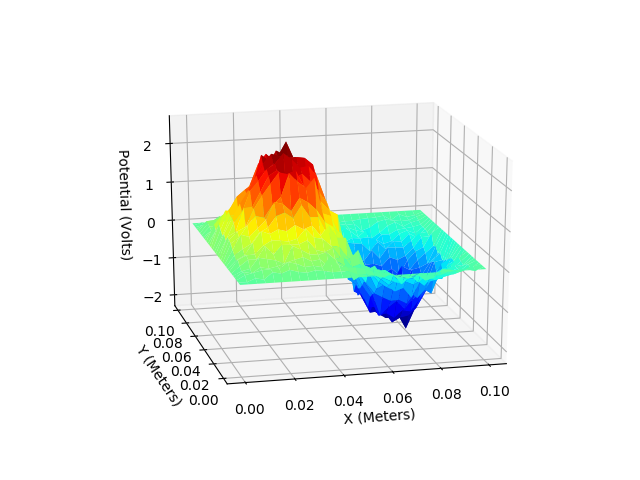
G. Two dimentional metal box with a two oppositely charged spheres (Poisson Equation)
H.Two dimentional metal box with a spherical charge at center using semi-floating random walk algorithm (Poisson Equation)
I. Two dimentional metal box with a spherical charge at center using full floating random walk algorithm (Poisson Equation)