foambryo

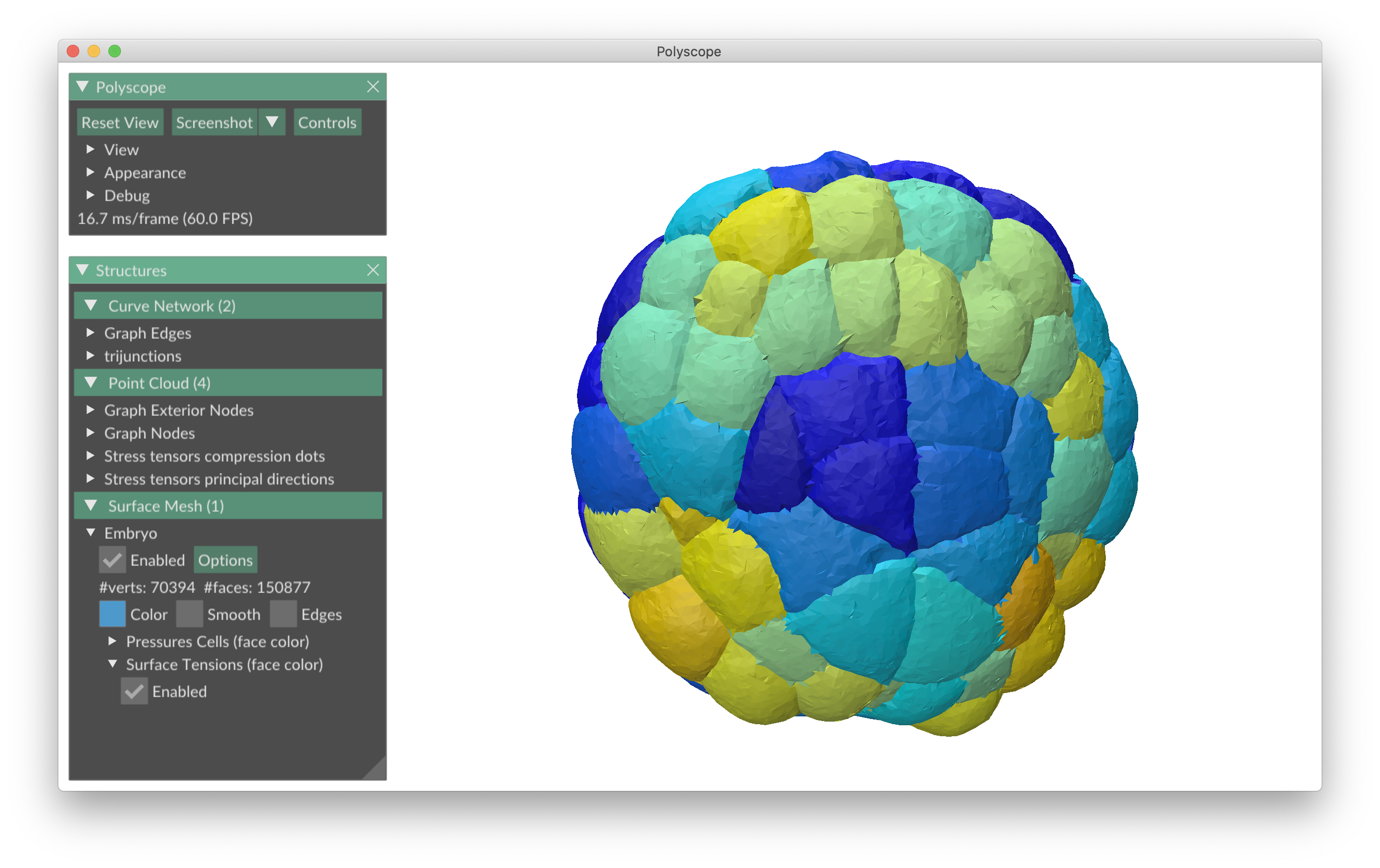
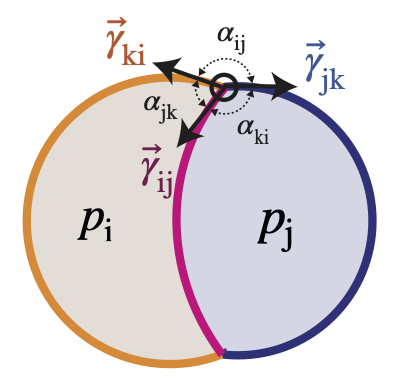
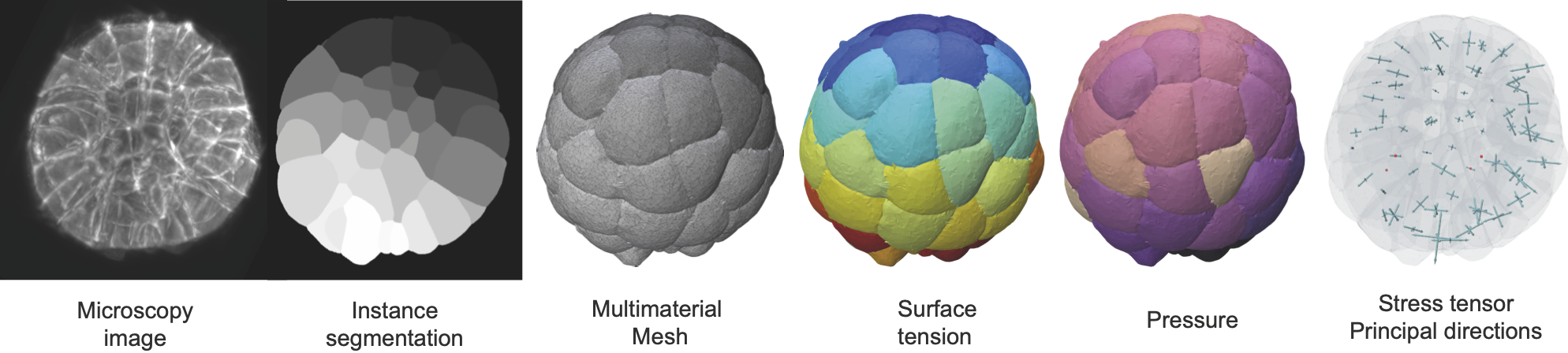
foambryo is a python package developed to infer relative surface tensions and cell pressures from the 3D geometry of cells in foam-like clusters, such as early-embryos, tissues or organoids.

It was developed by Sacha Ichbiah during his PhD in Turlier Lab, and is maintained by Sacha Ichbiah and Hervé Turlier. For support, please open an issue. If you use our library in your work please cite the paper.

If you are interested in inferring tensions in 2D, please look at the foambryo2D package instead.

Biological and biophysical context

Multicellular structures encountered in the field of developmental biology have various shapes and arrangements that reflectes their physiological functions. Mechanics is at the heart of the development of these structures, yet tools to investigate the forces at play in 3D remain scarse. Inferring forces or stresses from cell shapes only allows one to reveal the fundamental mechanics shaping cells from microscopy imaging. This software makes the hypothesis that cells in many early embryos, tissues and cell aggregates are mechanically akin to heterogeneous foam-like structures (see Physical model).

Prerequisites

foambryo requires Python >3.6 with pip.

foambryo requires the prior segmentation of images of multicellular aggregates into cell segmentation masks using one's favorite algorithm (watershed algorithm, cellpose or any preferred one). The quality of the segmentation and the size of the original image will directly affect the precision of the inference results.

Dependencies

All required dependencies are installed by pip automatically.

foambryo relies on a companion tool delaunay-watershed that we developed to construct precise multimaterial meshes from instance segmentations. From these multimaterial meshes, one can efficiently and robustly measure junction angles and interface curvatures to invert the Young-Dupré and Laplace laws and infer the surface tensions $\gamma_{ij}$ and cell pressures $p_i$ underlying the mechanical equilibrium of foam-like cell aggregates.

The viewer is based on Polyscope, a C++/Python viewer designed to visualize 3-dimensional geometrical, in particular meshes.

Operating systems

This package should work on any OS and was tested on the following macOS and Linux systems:

macOS: BigSur (11.7.9) and Ventura (13.5)

Linux: Ubuntu 16.04, CentOS 7 and Manjaro 22.0

Installation

We recommend to install foambryo from the PyPI repository directly

pip install foambryo

For developers, you may also install foambryo by cloning the source code and installing from the local directory

git clone https://github.com/VirtualEmbryo/foambryo.git
pip install pathtopackage/foambryo

Quick start example

Load an instance segmentation, reconstruct its multimaterial mesh, infer and visualize the forces with Polyscope

from dw3d import DCEL_Data, geometry_reconstruction_3d
from foambryo import plot_force_inference, plot_tension_inference

## Load the labels
import skimage.io as io
Segmentation = io.imread("Segmentation.tif")

## Reconstruct a multimaterial mesh from the labels
DW = geometry_reconstruction_3d(Segmentation,min_dist = 5)
Verts, Faces_multimaterial = DW.return_mesh()
Mesh = DCEL_Data(Verts,Faces_multimaterial)

## Infer and view the forces
plot_force_inference(Mesh)

#Or just the tensions
plot_tension_inference(Mesh)

Physical model

We consider a tissue constituted of cells i.

They minimize, under conservation of volume an energy $\mathcal{E}=\underset{ij}{\sum}\gamma_{ij}$.

The two main laws underlying mechanical force balance are:

Young-Dupré Law: $\gamma_{ij} + \gamma_{ik} + \gamma_{jk} = 0$.
Laplace Law: $p_j - p_i = 2 \gamma_{ij} H_{ij}$ where $H_{ij}$ is the mean curvature of the interface between the cell i and j.

API and Documentation

1 - Loading a multimaterial mesh

The first step is to load your multimaterial mesh into a DCEL_Data object via the builder DCEL_Data(Verts, Faces_multimaterial). - Verts is a V x 3 Numpy array of vertex positions, where V is the number of vertices. - Faces_multimaterial is a F x 5 numpy array of F faces (triangles) and labels, where at each row the 3 first indices refers to the indices of the three vertices of that triangle and the 2 last refer to a given interface label. An interface label is made of two indices referring to the two materials (e.g. cells) lying on each of its side, 0 being the exterior by convention.

2 - Infer tensions and pressures

Then the second step is to use this Mesh object to infer the relative surface tensions and cell pressures

infer_tension(Mesh,mean_tension=1,mode='YD'): One infers relative tensions by inverting mechanical equilibrium at each tri-material/cellular junction
- Mesh is a DCEL_Data object.
- mean_tension has to be defined as one only infers ratios between tensions, you can set it to 1 for instance.
- mode is the formula used to infer the tensions from contact angles at each junction. It has to be choosen among: YD (Young-Dupré with cosines only), Eq, Projection_YD (Young-Dupré with cosines and sines), cotan (cotangent formula, see Yamamoto et al. 2023), inv_cotan (inverse of the cotangent formula), Lamy (Lamy's theorem), inv_Lamy (inverse of the Lamy's relation), Lamy_Log (logarithm of the Lamy's relation), Variational (variational formulation, see our paper)
infer_pressures(Mesh,dict_tensions,mode='Variational', P0 = 0): We infer pressures relative to the exterior pressure $P_0$ by inverting normal force balance at each interface
- Mesh is a DCEL_Data object.
- dict_tensions is the dictionnary obtained with infer_tension.
- P0 has to be defined as one only pressures relative to the exterior.
- mode is the formula used to infer the pressures. It has to be choosen among: Variational (variational formulation, see our paper), Laplace (Laplace's law).

3 - Visualize

The viewer part of the package is built around several functions, each of them taking as an entry a Mesh object:

plot_tension_inference(Mesh,dict_tensions=None,alpha = 0.05, scalar_quantities = False, scattered = False, scatter_coeff=0.2): Which plots surface tensions by inverting Young-Dupré relations
- Mesh is a DCEL_Data object
- dict_tensions is the dictionnary obtained with infer_tension, and is computed automatically if unspecified.
- alpha : p_value threshold when displaying values: Values beyond the alpha and 1-alpha quantiles are clipped
- scalar_quantities: plot of vertex volume and area derivatives, of mean, Gaussian curvatures, and principal curvatures discrepancy. Can be quite long for big meshes
- scattered: scattered view of the mesh
- scatter_coeff: amount of displacement if scattered is activated
plot_force_inference(Mesh,dict_tensions = None, dict_pressure = None,alpha = 0.05, scalar_quantities = False, scattered = False, scatter_coeff=0.2): Which plots surface tensions, pressures and principal directions of the stress tensor
- Mesh is a DCEL_Data object
- dict_tensions is the dictionnary obtained with infer_tension, and is computed automatically if unspecified.
- dict_pressure is the dictionnary obtained with infer_pressure, and is computed automatically if unspecified.
- alpha : p_value threshold when displaying values: Values beyond the alpha and 1-alpha quantiles are clipped
- scalar_quantities: plot of vertex volume and area derivatives, of mean, gaussian curvatures, and principal curvatures discrepancy. Can be quite long for big meshes
- scattered: scattered view of the mesh
- scatter_coeff: amount of displacement if scattered is activated
plot_valid_junctions(Mesh): Valid junctions are plotted in green, and unstable junctions are plotted in red. This is used to assess the validity of the inference
- Mesh is a DCEL_Data object

Biological examples

P. mammillata early embryo

Phallusia mammillata is a solitary marine tunicate of the ascidian class known for its stereotypical development. As the embryo develops freely, without any constraint, we can do a full force inference and infer its tensions, pressures and stresses. We use segmentation data from Guignard, L., Fiúza, U. et al.

C. elegans early embryo

Caenorhabditis elegans is a widely studied model organism, with one of the most reproducible development. The embryo of this earthworm is developing within a shell. As the shell shape and mechanics is unknown, the pressures are not accessible. However we can still use Young-Dupré relationships to retrieve surface tensions at cell membranes. Here we use segmentation data from Cao, J., Guan, G., Ho, V.W.S. et al.

Plotting scalar quantities on surface meshes

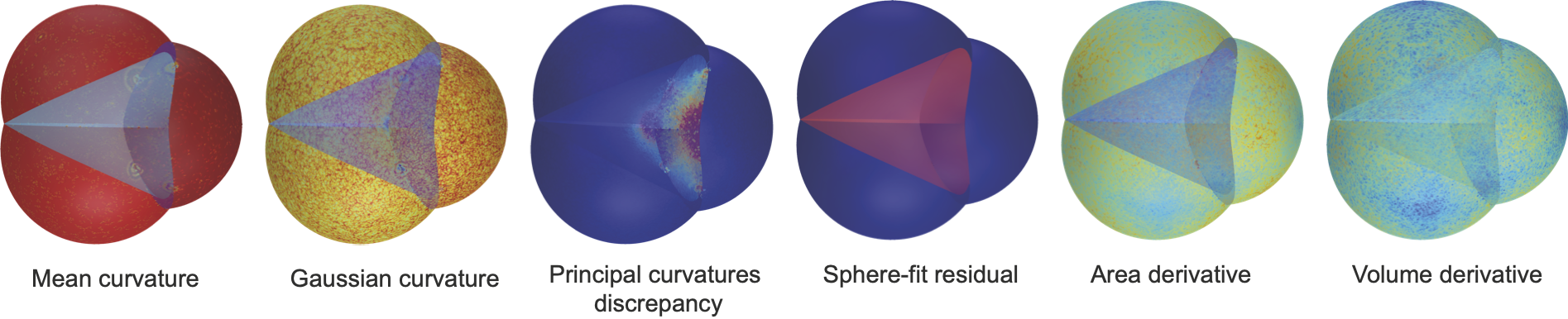
Gaussian and mean curvatures can be plotted on our meshes, and may be useful to study the geometric properties of interfaces between cells. We can also plot the vertex area and volume derivatives, that appear in our variational formulas, the difference between the two principal curvatures and the residual of the best sphere-fit that can be used to detect non-spherical constant-mean-curvature surfaces. They can be obtained by putting the option scalar_quantities = True when viewing the forces.

Gaussian Curvature is computed using the angle defect formula.
Mean Curvature is computed using the cotan formula.

To see the code of each of these use-cases, please load the associated jupyter notebooks in the folder Notebooks

Credits, contact, citations

If you use this tool, please cite the associated preprint: Do not hesitate to contact Sacha Ichbiah and Hervé Turlier for practical questions and applications. We hope that foambryo could help biologists and physicists to shed light on the mechanical aspects of early development.

@article {Ichbiah2023.04.12.536641,
	author = {Sacha Ichbiah and Fabrice Delbary and Alex McDougall and R{\'e}mi Dumollard and Herv{\'e} Turlier},
	title = {Embryo mechanics cartography: inference of 3D force atlases from fluorescence microscopy},
	elocation-id = {2023.04.12.536641},
	year = {2023},
	doi = {10.1101/2023.04.12.536641},
	publisher = {Cold Spring Harbor Laboratory},
	abstract = {The morphogenesis of tissues and embryos results from a tight interplay between gene expression, biochemical signaling and mechanics. Although sequencing methods allow the generation of cell-resolved spatio-temporal maps of gene expression in developing tissues, creating similar maps of cell mechanics in 3D has remained a real challenge. Exploiting the foam-like geometry of cells in embryos, we propose a robust end-to-end computational method to infer spatiotemporal atlases of cellular forces from fluorescence microscopy images of cell membranes. Our method generates precise 3D meshes of cell geometry and successively predicts relative cell surface tensions and pressures in the tissue. We validate it with 3D active foam simulations, study its noise sensitivity, and prove its biological relevance in mouse, ascidian and C. elegans embryos. 3D inference allows us to recover mechanical features identified previously, but also predicts new ones, unveiling potential new insights on the spatiotemporal regulation of cell mechanics in early embryos. Our code is freely available and paves the way for unraveling the unknown mechanochemical feedbacks that control embryo and tissue morphogenesis.Competing Interest StatementThe authors have declared no competing interest.},
	URL = {https://www.biorxiv.org/content/early/2023/04/13/2023.04.12.536641},
	eprint = {https://www.biorxiv.org/content/early/2023/04/13/2023.04.12.536641.full.pdf},
	journal = {bioRxiv}
}

License

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

sacha-ichbiah/foambryo