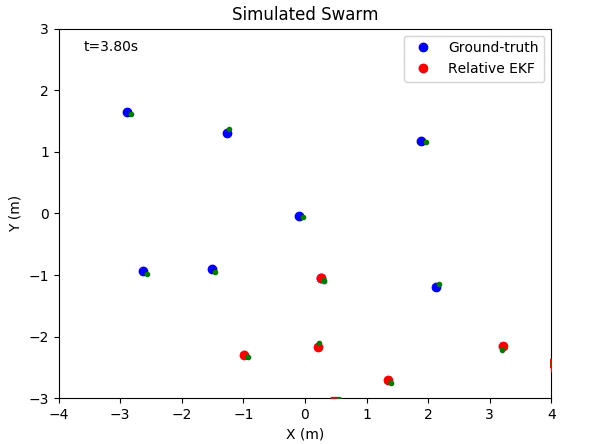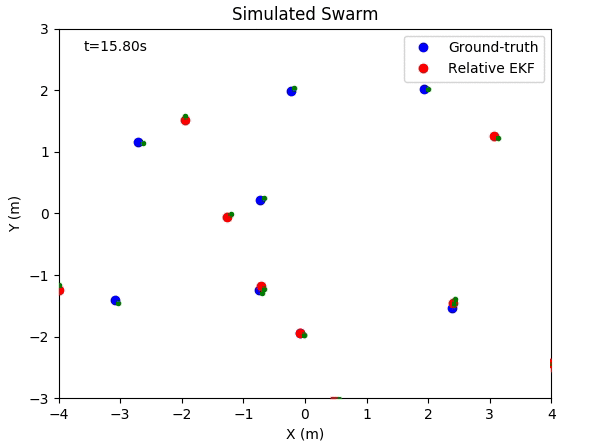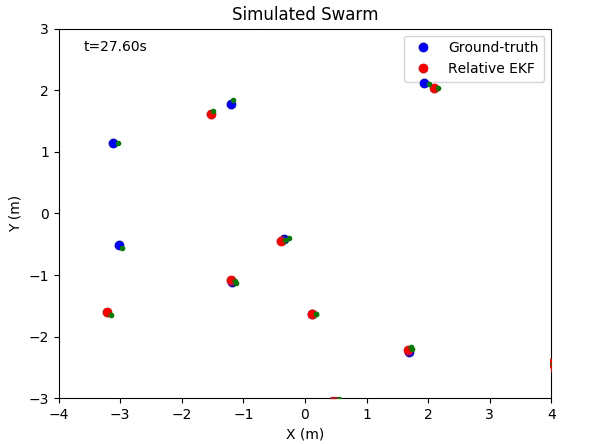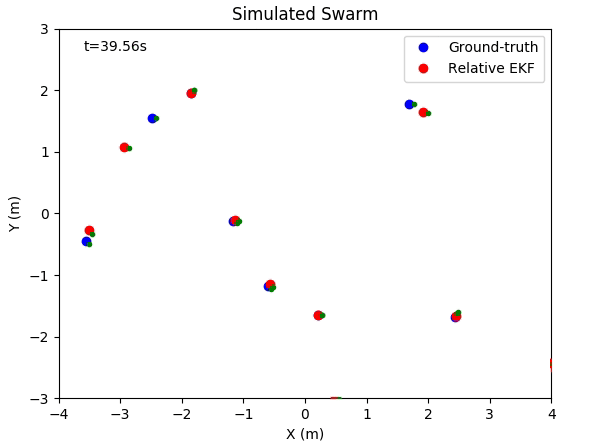
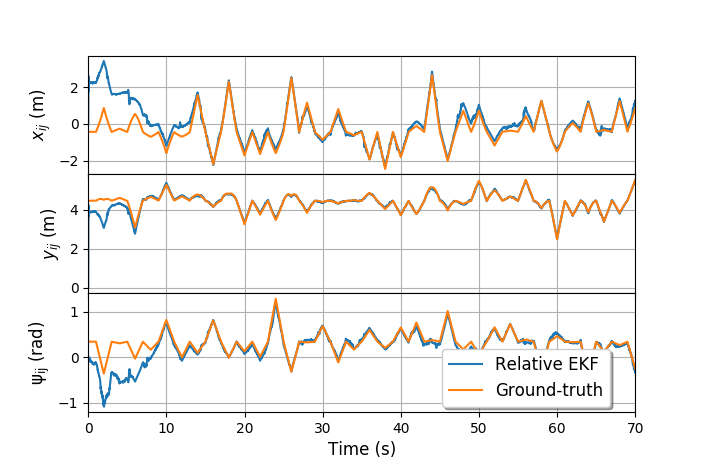
This project contains simulation code and real-world dataset to show the relative localization performance between multiple robots. This simulation is built in Python, which supports both animation and figure plot.
Paper: PDF on arXiv.
Video: Real-world flight on Youtube.
Quadrotor's code: Github link.
- Python 3.x
- matplotlib
- numpy
- csv
- statistics
$ git clone https://github.com/shushuai3/multi-robot-localization
$ cd multi-robot-localization
$ python3 main_simulation.py
- /dataset/dat01.csv: 3 crazyflie
- /dataset/dat02.csv: 3 crazyflie
- /dataset/dat03.csv: 4 crazyflie
- /dataset/dat01old.csv: 3 crazyflie & 160-second flight
- /dataset/dat02old.csv: 3 crazyflie & 120-second flight
- /dataset/dat03old.csv: 4 crazyflie & 160-second flight
- /dataset/dat04old.csv: 4 crazyflie & 160-second flight
timetick(ms) | velocity_x_robot0(m/s) | velocity_y_robot0(m/s) | yawRate_robot0(rad/s) | height_robot0(m) | distance_robot0_to_robot0(m) | distance_robot0_to_robot1(m) | distance02(m) | distance03(m) | distance04(m) |
vx1(m/s) | vy1(m/s) | r1(rad/s) | h1(m) | d10(m) | d11(m) | d12(m) | d13(m) | d14(m) | vx2(m/s) | vy2(m/s) | r2(rad/s) | h2(m) | d20(m) | d21(m) | d22(m) | d23(m) | d24(m) | vx3(m/s) | vy3(m/s) | r3(rad/s) | h3(m) | d30(m) | d31(m) | d32(m) | d33(m) | d34(m) | vx4(m/s) | vy4(m/s) | r4(rad/s) | h4(m) | d40(m) | d41(m) | d42(m) | d43(m) | d44(m) |
posX_robot0_optiTrack(m) | posY_robot0_optiTrack(m) | posZ_robot0_optiTrack(m) | quaternion1_robot0_optiTrack | quaternion2_robot0_optiTrack |quaternion3_robot0_optiTrack | quaternion4_robot0_optiTrack |
x1opti | y1opti | z1opti | q1Rob1 | q2Rob1 | q3Rob1 | q4Rob1 | x2opti | y2opti | z2opti | q1Rob2 | q2Rob2 | q3Rob2 | q4Rob2 | x3opti | y3opti | z3opti | q1Rob3 | q2Rob3 | q3Rob3 | q4Rob3 | x4opti | y4opti | z4opti | q1Rob4 | q2Rob4 | q3Rob4 | q4Rob4 |