Advanced Lane Finding Project
The goals / steps of this project are the following:
- Compute the camera calibration matrix and distortion coefficients given a set of chessboard images.
- Apply a distortion correction to raw images.
- Use color transforms, gradients, etc., to create a thresholded binary image.
- Apply a perspective transform to rectify binary image ("birds-eye view").
- Detect lane pixels and fit to find the lane boundary.
- Determine the curvature of the lane and vehicle position with respect to center.
- Warp the detected lane boundaries back onto the original image.
- Output visual display of the lane boundaries and numerical estimation of lane curvature and vehicle position.
Rubric Points
Here I will consider the rubric points individually and describe how I addressed each point in my implementation.
You're reading it!
1. Briefly state how you computed the camera matrix and distortion coefficients. Provide an example of a distortion corrected calibration image.
The code for this step is contained in the first code cell of the IPython notebook located in jupyter notebook pipeline.ipynb .
I start by preparing "object points", which will be the (x, y, z) coordinates of the chessboard corners in the world. Here I am assuming the chessboard is fixed on the (x, y) plane at z=0, such that the object points are the same for each calibration image. Thus, objp is just a replicated array of coordinates, and objpoints will be appended with a copy of it every time I successfully detect all chessboard corners in a test image. imgpoints will be appended with the (x, y) pixel position of each of the corners in the image plane with each successful chessboard detection.
I then used the output objpoints and imgpoints to compute the camera calibration and distortion coefficients using the cv2.calibrateCamera() function. I applied this distortion correction to the test image calibration5.jpg using the cv2.undistort() function and obtained this result:
We can the effect of undistortion is very obvious.
To demonstrate this step, I apply the distortion correction to one of the test images test5.jpg:
We can see the effect of undistortion is much harder to see than on the chessboard, these two pictures need to be viewer in a image viewer or consecutive web browser tabs to see the difference of lanes.
2. Describe how (and identify where in your code) you used color transforms, gradients or other methods to create a thresholded binary image. Provide an example of a binary image result.
I started with the example code of course video, which combining
Sobel X gradient and S channel of HSL color space. The result thresholded image is not good if the lane has sunshine on it.
(in project video 22 and 39 seconds )

Then I tried with different combinations of thresholding with channels RGB HSL HSV color space, and I found that the combination of R, G channel of RGB and L channel of HSL worked for the sunny lane.
The function is def thresholding(img): in cell 6 of the same notebook pipeline.ipynb.
3. Describe how (and identify where in your code) you performed a perspective transform and provide an example of a transformed image.
The code for my perspective transform includes a function called warp_image(), which appears in cell 7 in the same notebook pipeline.ipynb. The warp_image() function takes as inputs an image (colorgrad), as well as source (src) and destination (dst) points, and transform the image into a "birds-eye view" image.
I tried to think of a way to automatically decide the src points but failed, so I experimented with different hardcoded src and dst and plot them with cv2.polylines to help myself get a better src fitting the lane.
The hardcode the source and destination points are as following:
top_left = [570, 470]
top_right = [720, 470]
bottom_right = [1130, 720]
bottom_left = [200, 720]
src = np.array([bottom_left, bottom_right, top_right, top_left])
top_left_dst = [320, 0]
top_right_dst = [980, 0]
bottom_right_dst = [980, 720]
bottom_left_dst = [320, 720]
dst = np.array([bottom_left_dst, bottom_right_dst, top_right_dst, top_left_dst])This resulted in the following source and destination points:
| Source | Destination |
|---|---|
| 570, 470 | 320, 0 |
| 720, 470 | 980, 0 |
| 1130, 720 | 980, 720 |
| 200, 720 | 320, 720 |
I verified that my perspective transform was working as expected by drawing the src and dst points onto a test image and its warped counterpart to verify that the lines appear parallel in the warped image.
4. Describe how (and identify where in your code) you identified lane-line pixels and fit their positions with a polynomial?
In the function def fitlanes(): in the 8th code cell of the same notebook, I implemented the "sliding window" method introduced in the course video, which find the points in the warped image, and fit them with 2nd order polynomial using np.polyfit(lefty, leftx, 2).
The result image is like this:
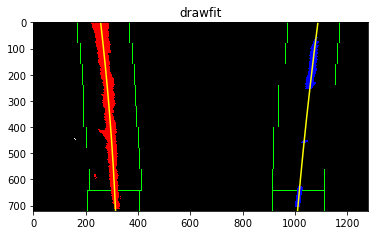
5. Describe how (and identify where in your code) you calculated the radius of curvature of the lane and the position of the vehicle with respect to center.
In the function drawfit(): of the same notebook I calculated the radius of curvature of the lane and the position of the vehicle with respect to center.
They are calculated by converting pixels to meters using an estimation of 30 meters / 720 pixels in y , and 3.7 meters(standard width of US lanes) / 700 pixels in x.
ym_per_pix = 30./720 # meters per pixel in y dimension
xm_per_pix = 3.7/700 # meters per pixel in x dimension
The car position in x axis and its offset to lane center can be calculated:
car_pos = binary_warped.shape[1] / 2
lane_center = (left_fitx[-1] + right_fitx[-1]) / 2
offset_in_meter = (lane_center - car_pos) * xm_per_pix
As the width of the lane is about 3.7 meter and center of the lane would be 3.7/2=1.85 approximately. For most of the time, value of car position with respect to center is in range (-0.5, 0.5), for the car being driving inside the lanes.
A test image showing the car has a slightly larger than 0.5m offset to the lane center:

6. Provide an example image of your result plotted back down onto the road such that the lane area is identified clearly.
I implemented this step in the function def drawwarpback():. Here is an example of my result on test-5.jpg:
1. Provide a link to your final video output. Your pipeline should perform reasonably well on the entire project video (wobbly lines are ok but no catastrophic failures that would cause the car to drive off the road!).
Here's a link to my video result
1. Briefly discuss any problems / issues you faced in your implementation of this project. Where will your pipeline likely fail? What could you do to make it more robust?
In my first few implementations my pipeline failed and 2 sections of lane with sunshine, and the detected lane curvature sometimes doesn't fit with real lanes. After I experimented with different thresholding combinations the problem was solved.
I tried to use the codes of edge detection and Hough transform from project 1 to help but failed.
I would like to try the challenge videos if I have more time.