CUDA/Cupy KD-Tree K-Nearest Neighbor Operator

This repository implements a KD-Tree on CUDA with an interface for cupy. It is a port of a previous implementation for tensorflow called tf_kdtree.

The KD-Tree is always generated using the CPU, but is automatically transferred to the GPU for cupy operations there. The KD-Tree implementation will search the k nearest neighbors of each queried point in logarithmic time and is best suited for repeated nearest neighbor queries in a static point cloud.

The algorithms' dimensions are currently defined through template parameters and must be known at compile-time. The present version compiles the library for the dimensionalities 1, 2, 3. See Compiling additional dimensions for instructions on how to compile additional dimensions.

Usage Examples

from cp_kdtree import build_kd_tree
import cupy as cp
from scipy.spatial import KDTree #Reference implementation
import numpy as np

#Dimensionality of the points and KD-Tree
d = 3

#Create some random point clouds
points_ref = np.random.uniform(size=(1000, d)).astype(np.float32) * 1e3
points_query = cp.random.uniform(size=(100, d)).astype(cp.float32) * 1e3

#Create the KD-Tree on the GPU and the reference implementation
cp_kdtree = build_kd_tree(points_ref, device='gpu')
kdtree = KDTree(points_ref)

#Search for the 5 nearest neighbors of each point in points_query
k = 5
dists, inds = cp_kdtree.query(points_query, nr_nns_searches=k)
dists_ref, inds_ref = kdtree.query(points_query.get(), k=k)

#Test for correctness 
#Note that the cupy_kdtree distances are squared
assert(np.all(inds.get() == inds_ref))
assert(np.allclose(cp.sqrt(dists).get(), dists_ref, atol=1e-5))

Installation

Prerequisites

Numpy (installed with setuptools)
Cupy (installed with setuptools)
Cuda
g++, or Visual Studio (MacOSX is untested)
CMake

Build Instruction

The easiest way of installing the library is using setuptools:

pip install .

Tests

After installation, you can run python -m pytest . inside the folder tests to verify that the library has been installed correctly.

Benchmark

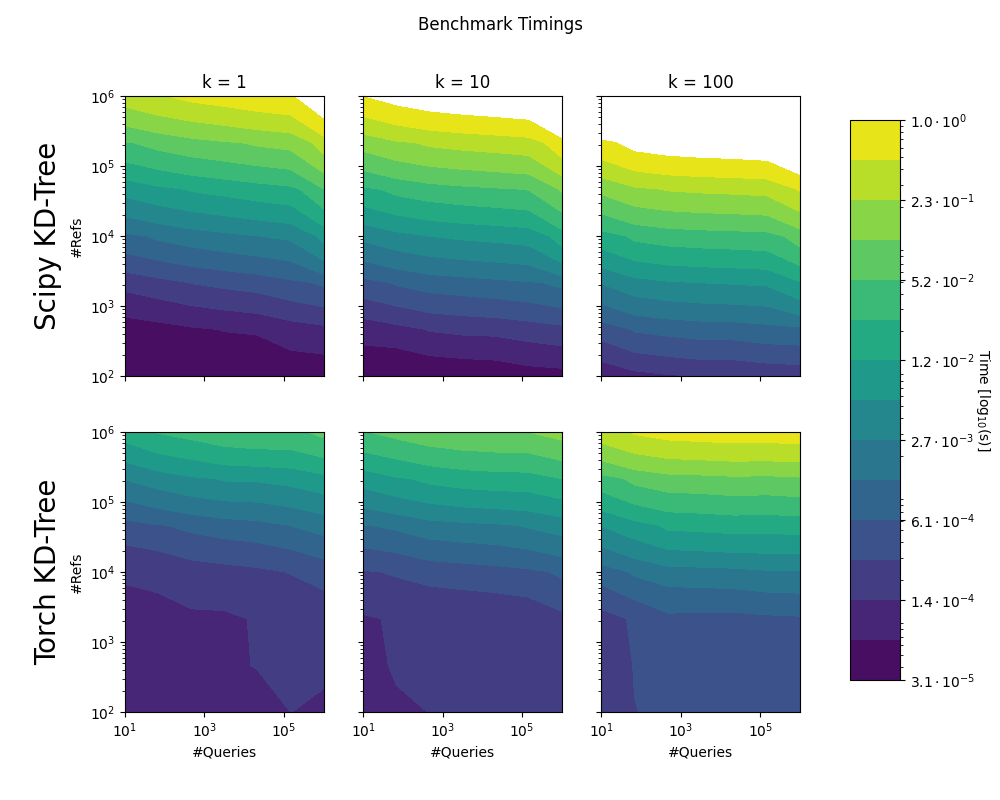
We compared the implementation to scipy.spatial.KDTree. Note that the benchmarks do not consider the time to build the KD-Trees, or the transfer to the GPU. Times greater than 1 second not shown.

Test Machine Specs: AMD Ryzen Threadripper 3970X 32x 3.7GHz, 128GB of working memory and a NVidia RTX 3090 GPU.

To run the benchmark on your computer, simply run python benchmark/benchmark.py. This will create benchmark_results.npz that can be converted to a figure using python benchmark/plot_benchmark.py (will require matplotlib).

Compiling additional dimensions

The dimension of the KD-Tree are compile time dynamic, meaning that the dimensions to be queried need to be known at compile time. By default, the library is compiled for d in [1, 2, 3]. You can add additional dimensions by adding new template dimensions to the pybind11 module in interface.cpp (line 115).

To add dimensionality 8 for example, you can add:

    KDTREE_INSTANTIATION(float, 8, false, "KDTreeCPU8DF");
    KDTREE_INSTANTIATION(double, 8, false, "KDTreeCPU8D");
    KDTREE_INSTANTIATION(float, 8, true, "KDTreeGPU8DF");
    KDTREE_INSTANTIATION(double, 8, true, "KDTreeGPU8D");

This will instantiate the template functions for float and double types both on the CPU and GPU.

Limitations

Int32 KNN indexing inside the library
Data must be cast to contiguous arrays before processing (automatically done by the library)
No in-place updates of the KD-Tree. If you modify the point-cloud, you will have to create a new KD-Tree.

Acknowledgements

If this works helps you in your research, please consider acknowledging the github repository, or citing our paper from which the library originated.

@article{grandits_geasi_2021,
	title = {{GEASI}: {Geodesic}-based earliest activation sites identification in cardiac models},
	volume = {37},
	issn = {2040-7947},
	shorttitle = {{GEASI}},
	url = {https://onlinelibrary.wiley.com/doi/abs/10.1002/cnm.3505},
	doi = {10.1002/cnm.3505},
	language = {en},
	number = {8},
	urldate = {2021-08-12},
	journal = {International Journal for Numerical Methods in Biomedical Engineering},
	author = {Grandits, Thomas and Effland, Alexander and Pock, Thomas and Krause, Rolf and Plank, Gernot and Pezzuto, Simone},
	year = {2021},
	keywords = {eikonal equation, cardiac model personalization, earliest activation sites, Hamilton–Jacobi formulation, inverse ECG problem, topological gradient},
	pages = {e3505}
}

thomgrand/cp_kdtree