A Smooth Representation of SO(3) for Deep Rotation Learning with Uncertainty

Valentin Peretroukhin, Matthew Giamou, David M. Rosen, W. Nicholas Greene, Nicholas Roy, and Jonathan Kelly

Robotics: Science and Systems (2020)

🏆 Best Student Paper Award Winner!🏆

Paper website: https://papers.starslab.ca/bingham-rotation-learning/
arXiv paper: https://arxiv.org/abs/2006.01031

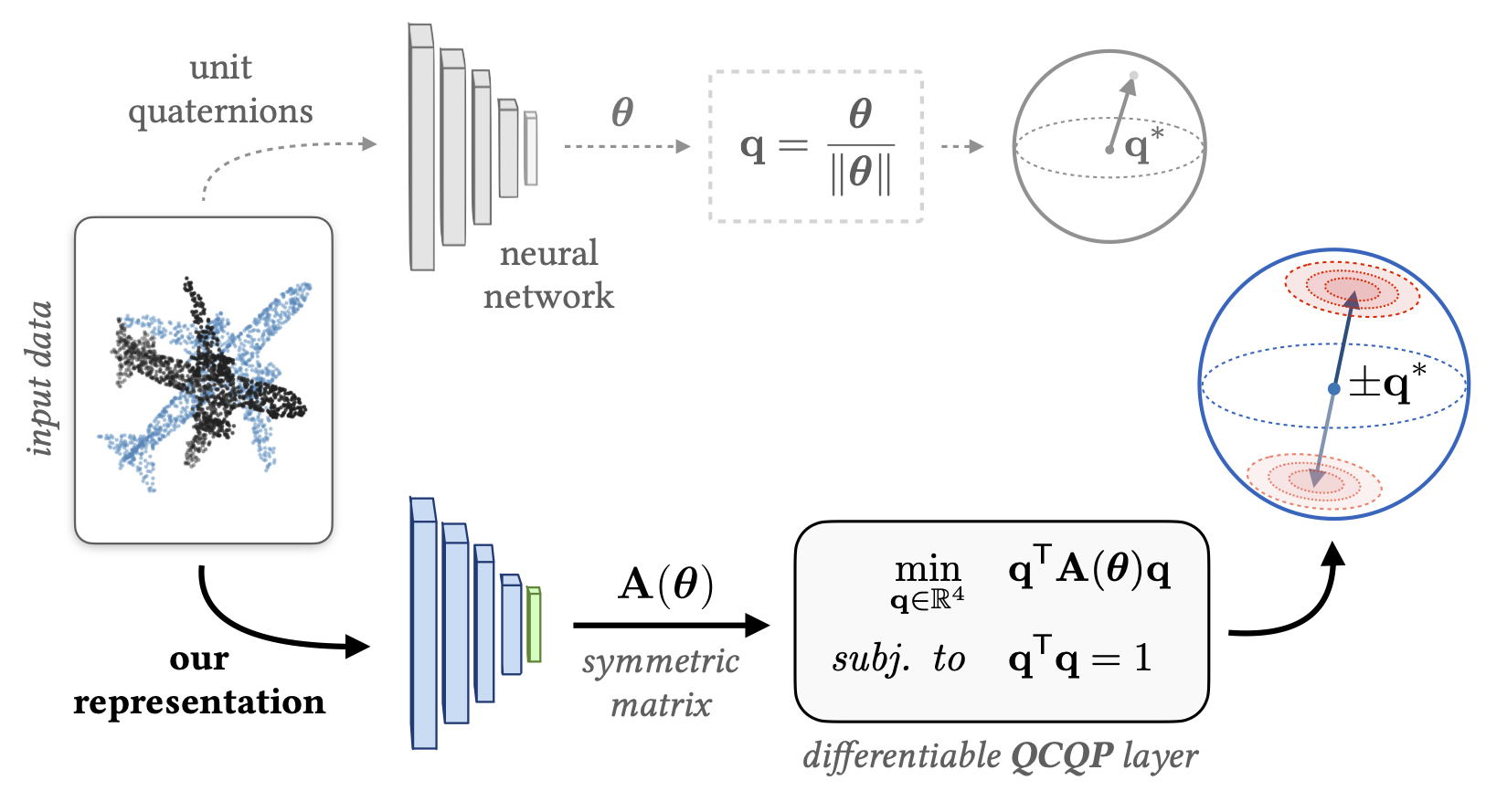
There are many ways to represent rotations including Euler angles, rotation matrices, axis-angle vectors, and unit quaternions. In deep learning applications, it is common to use unit quaternions for their simple geometric and algebraic structure. However, unit quaternions lack an important smoothness property that makes learning 'large' rotations difficult, and other representations are not easily amenable to learning uncertainty. In this work, we address this gap through a symmetric-matrix-based representation that is both smooth and defines a belief (or distribution) over rotations.

This repository contains example code to implement our representation in your work and all of our experiments from the paper (in pytorch).

Get Started

Prerequistes

Standard pip/conda stuff: numpy, scipy, torch, torchvision, argparse, matplotlib

Slightly less standard stuff: tqdm, tensorboardx

Finally we rely on our lab's Lie group library, liegroups (with bindings for pytorch/numpy), available here (unfortunately not yet on pip). You can install it via:

git clone https://github.com/utiasSTARS/liegroups.git

cd liegroups && pip install .

Run the script demo!

The demo will train three models on a synthetic point cloud dataset, with the unit quaternion, six dimensional representation (Zhou et. al, CVPR 2019 -- [41] in the paper), and our symmetric A representation.

python run_rotation_learning_demo.py

Run the `rss_demo.ipynb` notebook!

Note the additional dependancy lrcurve (for live plotting) You can see a list of options within the script.

Recreate our experiments

See the experiments folder for all of our experimental scripts (you will need to download raw KITTI and ShapeNet files). To regenerate our plots, there are also several readme plots that contain Google Drive links with cached data.

Use Our Representation in Your Work

Our representation is very easy to use for any rotation learning!

Create a network that outputs 10-vectors (i.e., Bx10 matrices for a minibatch size B).
Create a function that converts each 10-vector into a symmetric 4x4 matrix (Bx4x4). We have written a function convert_Avec_to_A() which you can steal! The file qcqp_layers.py contains this function as well as some other (batch-ified) helper functions that may be useful.
To convert each 4x4 symmetric matrix into a unit quaternion, simply apply torch.symeig() and extract the eigenvector corresponding to the smallest eigenvalue. This function can be a simple as:
```
def A_vec_to_quat(A_vec):
    A = convert_Avec_to_A(A_vec)
    _, evs = torch.symeig(A, eigenvectors=True)
    return evs[:,:,0].squeeze()
```
Our version of this function (see qcqp_layers.py) has a small check for dimensionality but is otherwise identical to the one above. Note that we have also implemented a torch.autograd function with an explicit analytic gradient but the built-in pytorch differentiation of torch.symeig() results in identical performance. Feel free to use either.

This entire procedure can be implemented within your model. For example:

class RotationNet(torch.nn.Module):
    def __init__(self):
        super(RotationNet, self).__init__()
        self.net = GenericNet() #Outputs Bx10
    
    def A_vec_to_quat(self, A_vec):
        A = convert_Avec_to_A(A_vec) #Bx10 -> Bx4x4
        _, evs = torch.symeig(A, eigenvectors=True)
        return evs[:,:,0].squeeze()

    def forward(self, x):
        A_vec = self.net(x) #Bx10
        q = self.A_vec_to_quat(A_vec) #Bx10 -> Bx4
        return q #unit quaternions!

This incurs minimal (but non-zero) overhead and should improve training if you have `large' rotation targets (i.e., rotations close to 180 degrees about any axis).

Citation

If you use this in your work, please cite:

@inproceedings{peretroukhin_so3_2020,
   author={Valentin Peretroukhin and Matthew Giamou and David M. Rosen and W. Nicholas Greene and Nicholas Roy and Jonathan Kelly},
   title={A {S}mooth {R}epresentation of {SO(3)} for {D}eep {R}otation {L}earning with {U}ncertainty},
   booktitle={Proceedings of {R}obotics: {S}cience and {S}ystems {(RSS'20)}},
   year={2020},
   date = {2020-07-12/2020-07-16},
   month = {Jul. 12--16},
}

utiasSTARS/bingham-rotation-learning