This small package provides wrapper functions to evaluate average
evolvability measures in evolutionary quantitative genetics, based on
the implementation of recursion-based evaluation of moments of ratios of
quadratic forms in the package qfratio
(CRAN;
GitHub).
The package qfratio provides functions to evaluate moments of ratios
of quadratic forms in normal variables using recursive algorithms. That
package was originally developed for evaluating average evolvability
measures (Watanabe, 2023), but is capable of
evaluating moments in rather general conditions beyond those. The idea
of this package is to provide a simple, convenient interface
specifically aiming at average evolvability measures, by passing
appropriately specified arguments to functions from the qfratio
package. All average evolvability measures treated by Watanabe
(2023) are implemented, accommodating arbitrary
mean and covariance for the selection gradients.
As a supplement, this package also has functions to obtain Monte Carlo
samples for evolvability measures (including the random skewers
correlation), as well as the delta method approximations for average
evolvability measures by Hansen and Houle
(2008). Existing packages like evolvability
(CRAN) and evolqg
(GitHub) have these
functionalities, but this package’s implementation is more general
(Monte Carlo versions accommodate arbitrary mean and covariance) and
faster, at least as of writing this.
# install.packages("devtools")
devtools::install_github("watanabe-j/avrevol")Imports: qfratio, MASS
Here are hypothetical examples for typical use cases:
library(avrevol)
## Simple covariance matrices
nv <- 4
G1 <- diag(nv:1)
G2 <- diag(sqrt(1:nv))
nit <- 1000
## Average conditional evolvability using series expression
## Inspect plot to check for convergence
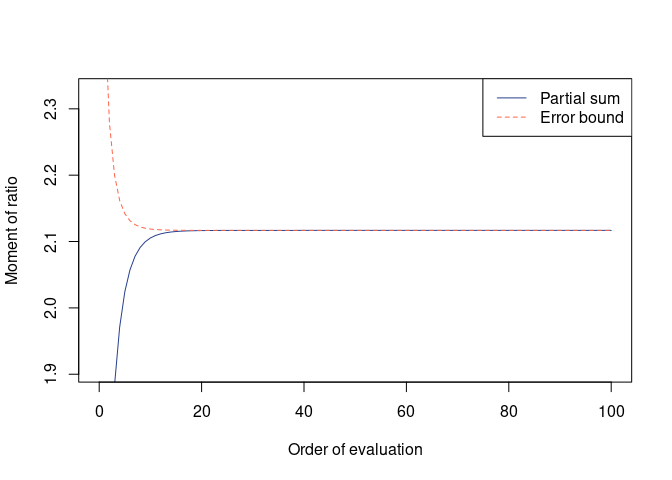
(res_cevo <- avr_cevo(G1))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 2.11678, Error = 2.768619e-15 (one-sided)
#> Possible range:
#> 2.11677962 2.11677962
plot(res_cevo)## Hansen & Houle's (2008) delta method approximation of the same
hh_cevo(G1)
#> [1] 2.11968
## Monte Carlo sample of conditional evolvability
## under spherical distribution of beta,
## and its mean as an estimate of average conditional evolvability
## plus its 95% CI
mcsample_cevo <- mc_cevo(nit, G1)
mean(mcsample_cevo)
#> [1] 2.104252
mean(mcsample_cevo) + sd(mcsample_cevo) / sqrt(nit) *
qt(c(0.025, 0.975), nit - 1)
#> [1] 2.064085 2.144419
## Average response difference using series expression,
## Hansen-Houle delta method approximation, and
## Monte Carlo estimate
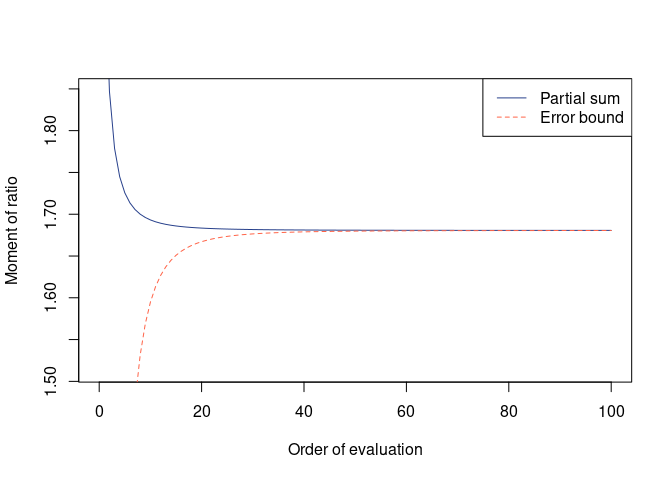
(res_rdif <- avr_rdif(G1, G2))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 1.680634, Error = -0.0001131094 (one-sided)
#> Possible range:
#> 1.68052050 1.68063361
plot(res_rdif)hh_rdif(G1, G2)
#> [1] 1.682945
mean(mc_rdif(nit, G1, G2))
#> [1] 1.673985
## Average response correlation using series expression and
## its Monte Carlo estimate, aka "random skewers" correlation
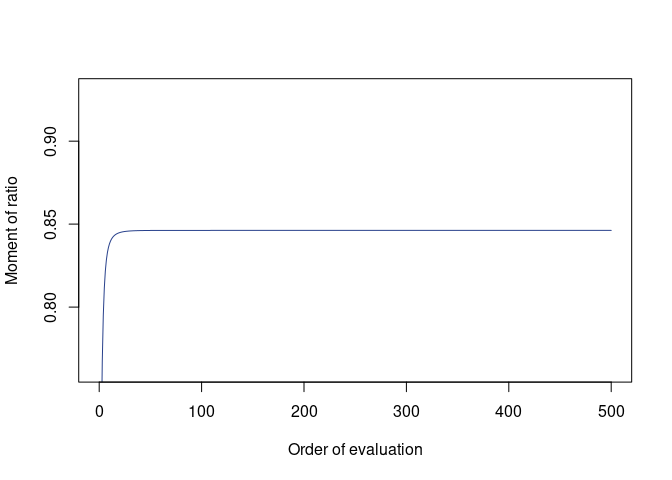
(res_rcor <- avr_rcor(G1, G2, m = 500))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 0.8462197
#> Error bound unavailable; recommended to inspect plot() of this object
plot(res_rcor)mean(mc_rcor(nit, G1, G2))
#> [1] 0.8479261
## Advanced: Average evolvability under
## non-spherical distribution of selection gradient
## (the same works for other evolvability measures as well)
mu <- nv:1 / nv
Sigma <- matrix(0.5, nv, nv)
diag(Sigma) <- 1
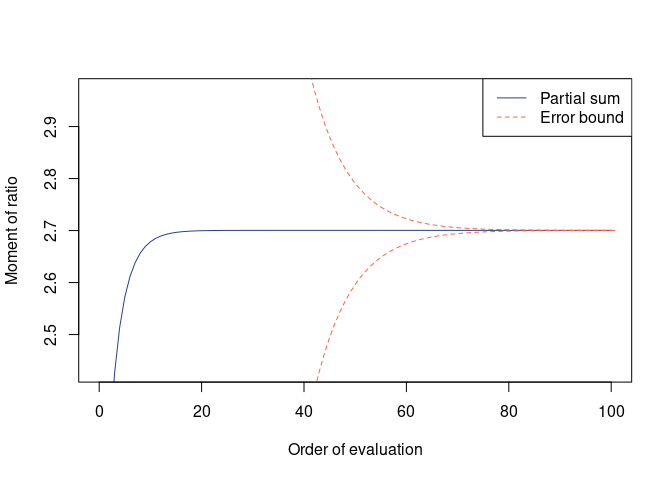
(res_evol_nsph <- avr_evol(G1, mu = mu, Sigma = Sigma))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 2.70034, Error = 5.948518e-05 (two-sided)
#> Possible range:
#> 2.70028007 2.70039904
plot(res_evol_nsph)mean(mc_evol(nit, G1, mu = mu, Sigma = Sigma))
#> [1] 2.715177Bolstad, G. H., Hansen, T. F., Pélabon, C., Falahati-Anbaran, M., Pérez-Baralles, R. and Armbruster, W. S. (2014) Genetic constraints predict evolutionary divergence in Dalechampia blossoms. Philosophical Transactions of the Royal Society B: Biological Sciences, 369, 20130255. doi:10.1098/rstb.2013.0255.
Hansen, T. F. and Houle, D. (2008) Measuring and comparing evolvability and constraint in multivariate characters. Journal of Evolutionary Biology, 21, 1201–1219. doi:10.1111/j.1420-9101.2008.01573.x.
Marroig, G., Shirai, L. T., Porto, A., Oliveira, F. B. de and De Conto, V. (2009) The evolution of modularity in the mammalian skull II: Evolutionary consequences. Evolutionary Biology, 36, 136–148. doi:10.1007/s11692-009-9051-1.
Melo, D., Garcia, G., Hubbe, A., Assis, A. P. and Marroig, G. (2016) EvolQG—an R package for evolutionary quantitative genetics [version 3; referees: 2 approved, 1 approved with reservations]. F1000Research, 4, 925. doi:10.12688/f1000research.7082.3.
Watanabe, J. (2023) Exact expressions and numerical evaluation of average evolvability measures for characterizing and comparing G matrices. Journal of Mathematical Biology, 86, 95. doi:10.1007/s00285-023-01930-8.