ggpcp
Generalized parallel coordinate plots with ggpcp
R package for creating generalized parallel coordinate plots in the ggplot2 framework
Installation
ggpcp is available from Github:
# install.packages("devtools")
remotes::install_github("yaweige/ggpcp", build_vignettes = TRUE)Getting Started
Load the library
library(ggpcp)Load a dataset
library(tidyverse)
data(flea, package = "GGally")A first parallel coordinate plot
The two main arguments for drawing a parallel coordinate plot are the
aesthetic vars and the parameter method.
With the aesthetic vars all variables are specified that are supposed
to go into the parallel coordinate plot. The specification uses the
dplyr function vars with the corresponding selectors.
You can specify variables by
- position, e.g.
1:4, 7, 5, 4, - name, e.g.
class,age,sex,aede1:aede3or - selector, e.g.
starts_with("aede"), see?tidyselect::select_helpers
or any combination thereof. Variables can be selected multiple times and will then show up multiple times in the plot.
method is a character string that determines the method to be used
when transforming the values of each variable into a common y axis. By
default, the method uniminmax is chosen, which univariately scales
each variable into a range of [0,1] with a minimum at 0 and the
maximum at 1. ‘?transform_pcp’ gives more details.
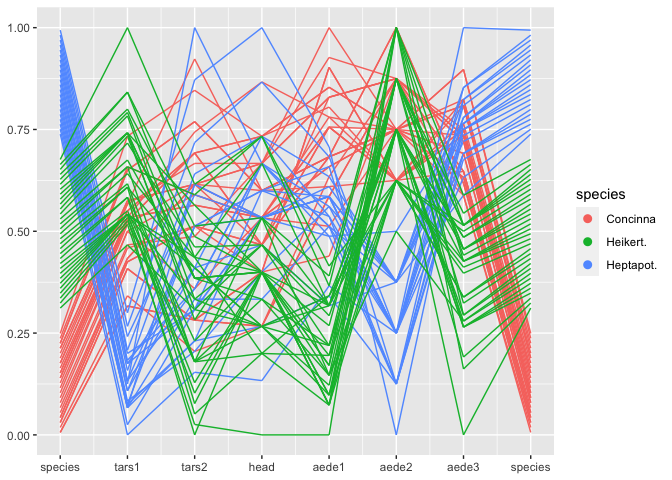
flea %>%
ggplot(aes(colour = species)) +
geom_pcp(aes(vars=vars(species, 2:7, species)))Note that the variable species shows up twice in the plot - once as
the rightmost variables, once as the leftmost one. species is a
categorical variable. ggpcp deals with categorical variables by using
the space on the y axis of a categorical variable to spread points out
evenly. This allows us to (a) estimate the frequency of each level, and
(b) track individual points through the parallel coordinate plot even in
the presence of categorical variables.
The layer approach
ggpcp implements several geoms to work in a parallel coordinate plot
setting
geom_pcpis a wrapper for the standard layer of drawing line segments for each observation across the specified variablesgeom_pcp_boxdraws rectangles framing each level of a categorical variable. The parameterboxwidthspecifies the width of these rectangles (1 is the width between successive variables).boxwidthis set to 0 by default.geom_pcp_textplaces a label center on each rectangle of a categorical variable. The familiar parametersnudge_xandnudge_ywork as usual to move labels.- … add as more geoms become available
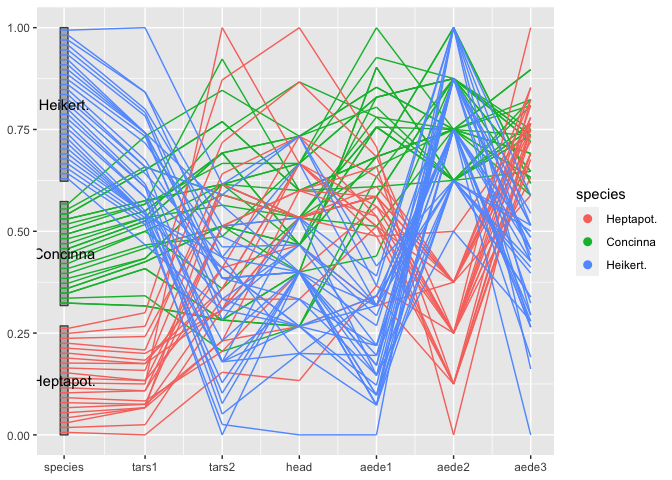
flea %>%
mutate(species = factor(species, levels = c("Heptapot.", "Concinna", "Heikert."))) %>%
ggplot(aes(vars = vars(1:7))) +
geom_pcp_box(boxwidth = 0.1, fill="grey70") +
geom_pcp(aes(colour=species), boxwidth = 0.1) +
geom_pcp_text(boxwidth = 0.1)Another look at the Titanic Data
For categorical variables ggpcp presents a result similar to parsets
by Kosara et al (2013).
titanic <- as.data.frame(Titanic)
titanic <- titanic %>%
purrr::map(.f = function(x) rep(x, titanic$Freq)) %>%
as.data.frame() %>% select(-Freq)
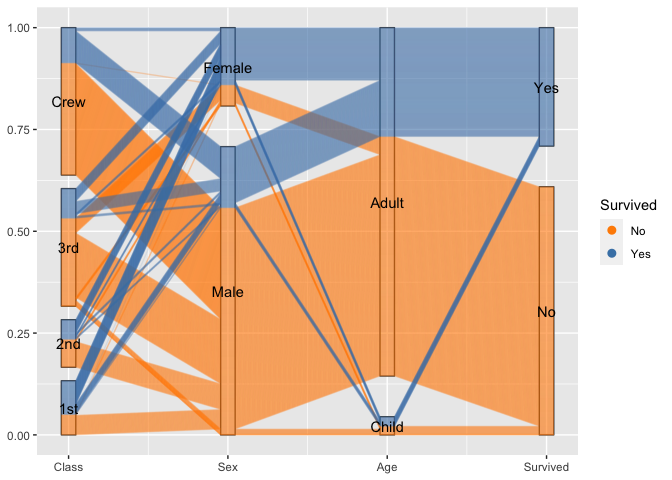
titanic %>%
ggplot(aes(vars=vars(1:4))) +
geom_pcp_box(boxwidth=0.1) +
geom_pcp(aes(colour = Survived), alpha = 0.1, boxwidth=0.1) +
scale_colour_manual(values=c("darkorange", "steelblue")) +
guides(colour=guide_legend(override.aes = list(alpha=1))) +
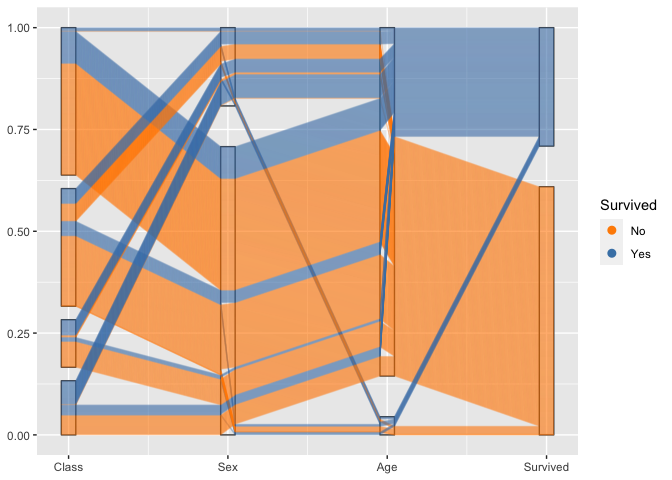
geom_pcp_text(boxwidth=0.1) By setting break points between blocks of categorical variables, we can focus on the two-dimensional relationship between variables on adjacent axes:
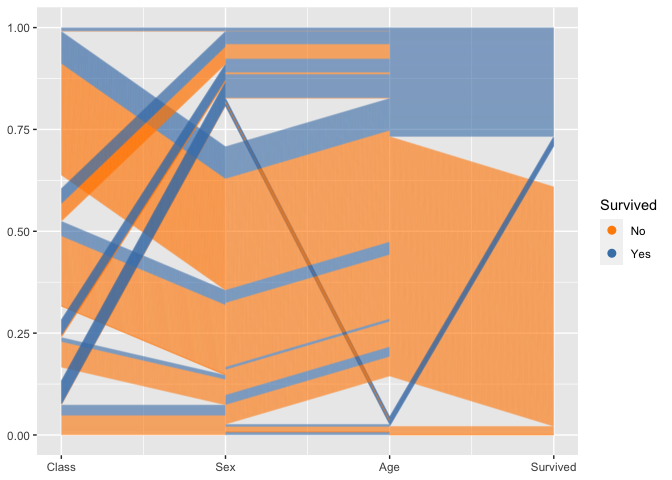
titanic %>%
ggplot(aes(vars = vars(1:4))) +
geom_pcp(aes(colour = Survived), alpha = 0.1, resort=2:3) +
scale_colour_manual(values=c("darkorange", "steelblue")) +
guides(colour=guide_legend(override.aes = list(alpha=1))) To combine the option of tracking individuals with the focus on 2d relationships between axes, we introduce a box for each axis to allow the tracking. For the thousands of people on board the Titanic individual tracking is tricky, but with good eyesight and a large screen still manageable :)
titanic %>%
ggplot(aes(vars=vars(1:4))) +
geom_pcp_box(boxwidth=0.1, fill=NA) +
geom_pcp(aes(colour = Survived), alpha = 0.1,
boxwidth=0.1, resort=2:3) +
scale_colour_manual(values=c("darkorange", "steelblue")) +
guides(colour=guide_legend(override.aes = list(alpha=1))) Mixed data: categorical and numeric variables
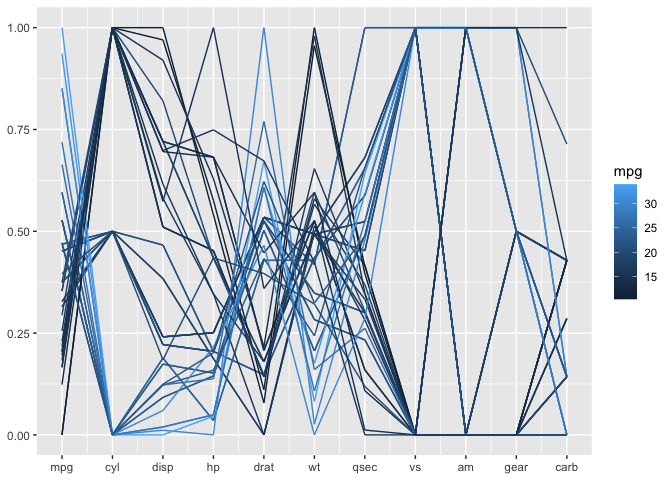
The mtcars data is terribly old, but serves a good purpose here. All
of the variables are coded as numeric variables, even when they should,
in fact, be factor variables. In a standard parallel coordinate plot we
get the usual uninformative fishnet between categorical variables such
as vs, am, and gear, also visible for variable cyl:
mtcars %>%
ggplot(aes(vars = vars(1:ncol(mtcars)))) +
geom_pcp(aes(colour = mpg)) Once the variables are coded properly as factor variables, we get a much more informative view with a generalized parallel coordinate plot:
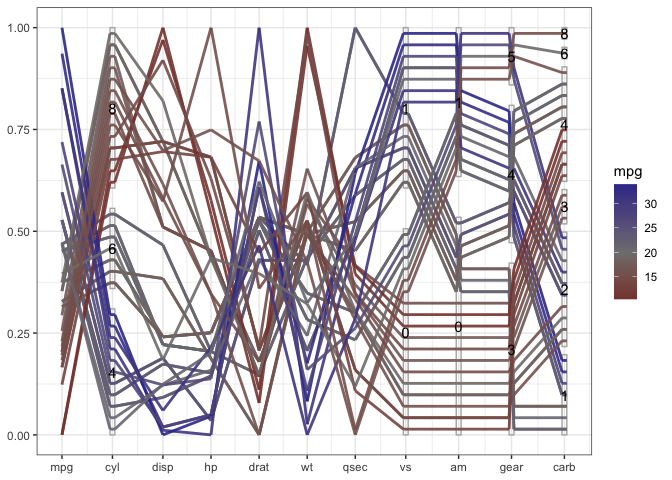
mtcars %>%
mutate(cyl = factor(cyl),
vs = factor(vs),
am = factor(am),
gear=factor(gear),
carb = factor(carb)) %>%
ggplot(aes(vars = vars(1:ncol(mtcars)))) +
geom_pcp_box(boxwidth=0.1, fill=NA, colour="grey70") +
geom_pcp(aes(colour = mpg), boxwidth=0.1, resort=9:10, size=1, alpha =0.9) +
geom_pcp_text(boxwidth=0.1) +
scale_colour_gradient2("mpg", mid="grey50", midpoint = 20) +
theme_bw()What becomes obvious in this plot, is that fuel consumption of each car measured in miles per gallons (mpg), encoded as the first variable in the plot and as color of the lines - is correlated strongly with all of the variables, not just the numeric variables. A large number of cylinders (cyl), a V-shaped engine (vs = 0), an automatic transmission (am = 0), a low number of forward gears and a high number of carburetors are related to a low value of mpg (red lines).
Bigger Example
One application for generalized parallel coordinate plots is their use for visualizing clusters.
data(nasa, package="ggpcp")The nasa data, made available as part of the ggpcp package provides
and extension to the data provided in the GGally package, was used in
the 2006 ASA Expo. It consists of monthly measurements of several
climate variables, such as cloud coverage, temperature, pressure, and
ozone values, captured on a 24x24 grid across Central America between
1995 and 2000.
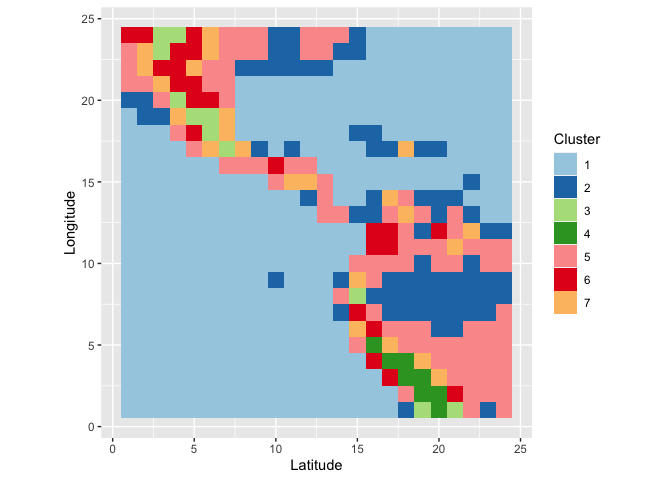
We grouped locations using all January and July measurements of all climate variables using a hierarchical clustering based on Ward’s distance. The resulting clusters can then be summarized visually. What we see is that the clusters have a very distinct geographic pattern (tile plot).
## `summarise()` has grouped output by 'id', 'variable'. You can override using the `.groups` argument.
wide %>% separate(id, into=c("y", "x"), remove = FALSE) %>%
mutate(x = as.numeric(x), y = as.numeric(y)) %>%
ggplot(aes(x = x, y=y, fill=factor(cl7))) +
geom_tile() + scale_fill_brewer("Cluster", palette = "Paired") +
xlab("Latitude") + ylab("Longitude") +
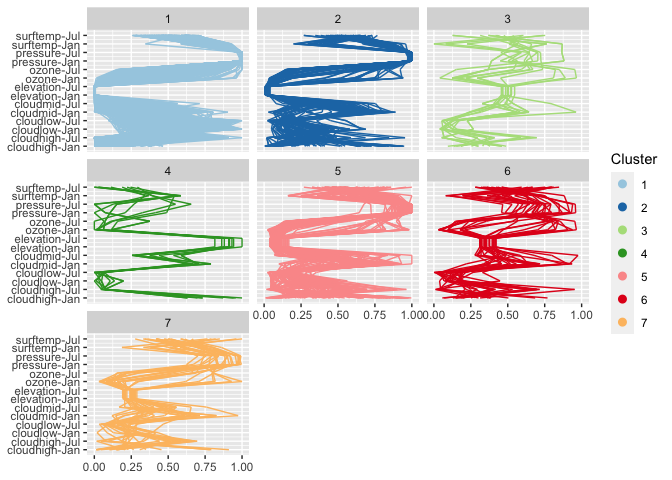
coord_equal()From the parallel coordinate plot we see that cloud coverage in low, medium and high altitude distinguishes quite succinctly between some of the clusters. (Relative) temperatures in January (1) and July (7) are very indicative to separate between clusters on the Southern and Northern hemisphere.
wide %>%
ggplot(aes(vars=vars(95:108))) +
geom_pcp(aes(colour=factor(cl7))) + facet_wrap(~cl7) +
coord_flip() + scale_colour_brewer("Cluster", palette = "Paired")Visualizing the cluster process
Needs more words …
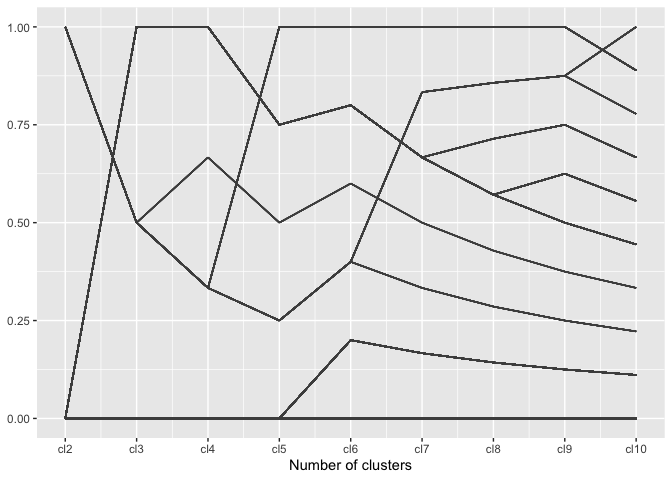
A regular parallel coordinate plot allows us to visualize a part of the dendrogram corresponding to the hierarchical clustering.
wide %>%
ggplot(aes(vars=vars(86:94))) +
geom_pcp() +
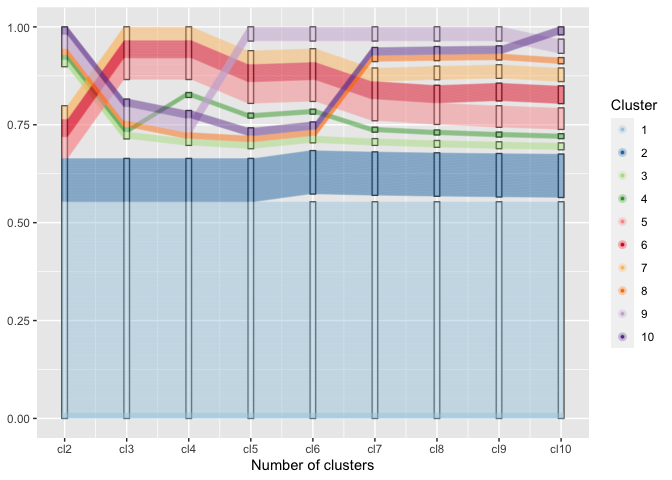
xlab("Number of clusters")Using the generalized parallel coordinate plots we can visualize the clustering process in plots similar to what Schonlau (2002, 2004) coined the clustergram:
wide %>%
mutate(
cl2 = factor(cl2),
cl3 = factor(cl3),
cl4 = factor(cl4),
cl5 = factor(cl5),
cl6 = factor(cl6),
cl7 = factor(cl7),
cl8 = factor(cl8),
cl9 = factor(cl9),
cl10 = factor(cl10)
) %>%
ggplot(aes(vars=vars(86:94), colour = factor(cl10))) +
geom_pcp_box(boxwidth=0.1) +
geom_pcp(alpha = 0.25, boxwidth=0.1) +
xlab("Number of clusters") +
scale_colour_brewer("Cluster", palette="Paired")Along the x-axis the number of clusters are plotted with one pcp axis each, from two clusters (left) to 10 clusters (right most pcp axis). Each observation is drawn as a multi-segmented line and colored by its assignment in the ten-cluster solution. This gives an excerpt of the dendrogram that allows an assessment of the number of observations in each cluster as well as the relationship between successive clustering steps.
Related work
Parallel coordinate plots have been implemented in analysis software since the mid 1980s (Inselberg 1985, Wegman 1990). Several packages in R are dedicated to visualizing parallel coordinate plots.
Using base plots the main function for drawing parallel coordinate plots
is parcoord implemented in MASS (Venables and Ripley 2004). The
package gclus (Hurley 2019) implements cparcoord to include panel
color as a representation of the strength of a correlation between
neighboring axes.
Within the ggplot2 environment there are several packages implementing
parallel coordinate plots. For numeric variables there’s the function
ggparcoord from the GGally package, for categorical variables the
ggparallel package provides an implementation of PCP-like plots, such
as the Hammock plot (Schonlau 2003) and parsets (Kosara et al, 2013).
The bigPint Google Summer of Code project 2017 implemented static and interactive versions of parallel coordinate plots within the framework of plotting large data interactively. These functions are meant for exploration and discovery and are not fully parameterized for their appearance.
Motivation for the Re-implementation
As can be seen from the examples above, there are a lot of approaches to parallel coordinate plots, so why do we need another implementation?
All of the implementations described above have in common that they describe highly specialized plots - in the sense that there are tens of parameters describing construction, type, and appearance of the plot. While giving the user some flexibility this way, this approach goes against the modular approach of the tidyverse, and in particular against the layered approach of ggplot2, i.e. at best the approaches make use of ggplot2, but they do not make use of the ideas behind ggplot2.
The main idea of ggpcp is that we separate the data transformations
from the visualization, i.e. rather than working with a single function
to draw a plot, we are providing a set of functions that work together.
This idea is not new - a function under the very same name was at some point part of ggplot2 (see https://www.rdocumentation.org/packages/ggplot2/versions/0.9.2.1/topics/ggpcp), but at the time the implementation stalled and was eventually removed from ggplot2.
References
- Hofmann H., Vendettuoli M.: Common Angle Plots as Perception-True Visualizations of Categorical Associations, IEEE Transactions on Visualization and Computer Graphics, 19(12), 2297-2305, 2013. doi: 10.1109/TVCG.2013.140
- Hurley C.: gclus: Clustering Graphics. R package version 1.3.2. https://CRAN.R-project.org/package=gclus
- Inselberg A., The Plane with Parallel Coordinates, The Visual Computer, 1(2), 69-91, 1985.
- Kosara R., Bendix F., Hauser H., Parallel Sets: Interactive Exploration and Visual Analysis of Categorical Data, IEEE Transactions on Visualization and Computer Graphics, 12(4), 558-568, 2006.
- Schloerke B., Crowley J., Cook D., Briatte F., Marbach M., Thoen E., Elberg ., Larmarange J.: GGally: Extension to ‘ggplot2’, R package version 1.4.0.
- Schonlau M.: Visualizing Categorical Data Arising in the Health Sciences Using Hammock Plots, Proc. of Section on Statistical Graphics ASA, 2003.
- Schonlau M. The clustergram: a graph for visualizing hierarchical and non-hierarchical cluster analyses. The Stata Journal, 2002; 2 (4):391-402.
- Schonlau M. Visualizing Hierarchical and Non-Hierarchical Cluster Analyses with Clustergrams. Computational Statistics: 2004; 19(1):95-111.
- Venables W.N., Ripley B.D.: Modern Applied Statistics with S (4th ed), Springer, 2002.
- Wegman, E., Hyperdimensional Data Analysis Using Parallel Coordinates, JASA, 85(411), 664-675, 1990.
- Wickham H., ggplot2: Elegant graphics for data analysis (2nd ed), Springer, 2016
- Wickham H., Tidy data. The Journal of Statistical Software, 59, 2014.
- Wilkinson L., The Grammar of Graphics. Statistics and Computing, Springer, 1999.