abspy: A Python repository from yhexie

Introduction

abspy is a Python tool for 3D adaptive binary space partitioning and beyond: an ambient 3D space is adaptively partitioned to form a linear cell complex with pre-detected planar primitives in a point cloud, where an adjacency graph is dynamically obtained. Though the tool is designed primarily to support compact surface reconstruction, it can be extrapolated to other applications as well.

Key features

Manipulation of planar primitives detected from point clouds
Linear cell complex creation with adaptive binary space partitioning (a-BSP)
Dynamic BSP-tree (NetworkX graph) updated locally upon insertion of primitives
Support of polygonal surface reconstruction from graph cuts
Compatible data structure with Easy3D on point clouds, primitives, cell complexes and surfaces
Robust Boolean spatial operations underpinned by the rational ring from SageMath's exact kernel

Installation

Install requirements

All dependencies except for SageMath can be easily installed with PyPI:

git clone https://github.com/chenzhaiyu/abspy && cd abspy
pip install -r requirements.txt

Optionally, install pyglet and pyembree for better visualisation and ray-tracing, respectively:

pip install pyglet pyembree

Install SageMath

For Linux and macOS users, the easiest is to install from conda-forge:

conda config --add channels conda-forge
conda install sage

Alternatively, you can use mamba for faster parsing and package installation:

conda install mamba
mamba install sage

For Windows users, you may have to build SageMath from source or install all other dependencies into a pre-built SageMath environment.

Install abspy

abspy itself can be found and easily installed via PyPI:

pip install abspy

Quick start

Here is an example of loading a point cloud in VertexGroup (.vg), partitioning the ambient space into candidate convexes, creating the adjacency graph, and extracting the outer surface of the object.

import numpy as np
from abspy import VertexGroup, AdjacencyGraph, CellComplex

# load a point cloud in VertexGroup 
vertex_group = VertexGroup(filepath='points.vg')

# normalise the point cloud
vertex_group.normalise_to_centroid_and_scale()

# additional planes to append (e.g., the bounding planes)
additional_planes = [[0, 0, 1, -bounds[:, 0, 2].min()]]

# initialise CellComplex from planar primitives
cell_complex = CellComplex(vertex_group.planes, vertex_group.bounds, vertex_group.points_grouped, build_graph=True, additional_planes=additional_planes)

# refine planar primitives
cell_complex.refine_planes()

# prioritise certain planes (e.g., vertical ones)
cell_complex.prioritise_planes(prioritise_verticals=True)

# construct CellComplex 
cell_complex.construct()

# print info on the cell complex
cell_complex.print_info()

# build adjacency graph of the cell complex
adjacency_graph = AdjacencyGraph(cell_complex.graph)

# assign weights (e.g., SDF values provided by neural network prediction) to graph 
weights_dict = adjacency_graph.to_dict(...)
adjacency_graph.assign_weights_to_n_links(cell_complex.cells, attribute='area_overlap', factor=0.001, cache_interfaces=True)
adjacency_graph.assign_weights_to_st_links(weights_dict)

# perform graph-cut to extract surface
_, _ = adjacency_graph.cut()

# save surface model to an OBJ file
adjacency_graph.save_surface_obj('surface.obj', engine='rendering')

Usage can be found at API reference. For the data structure of a .vg/.bvg file, please refer to VertexGroup.

Misc

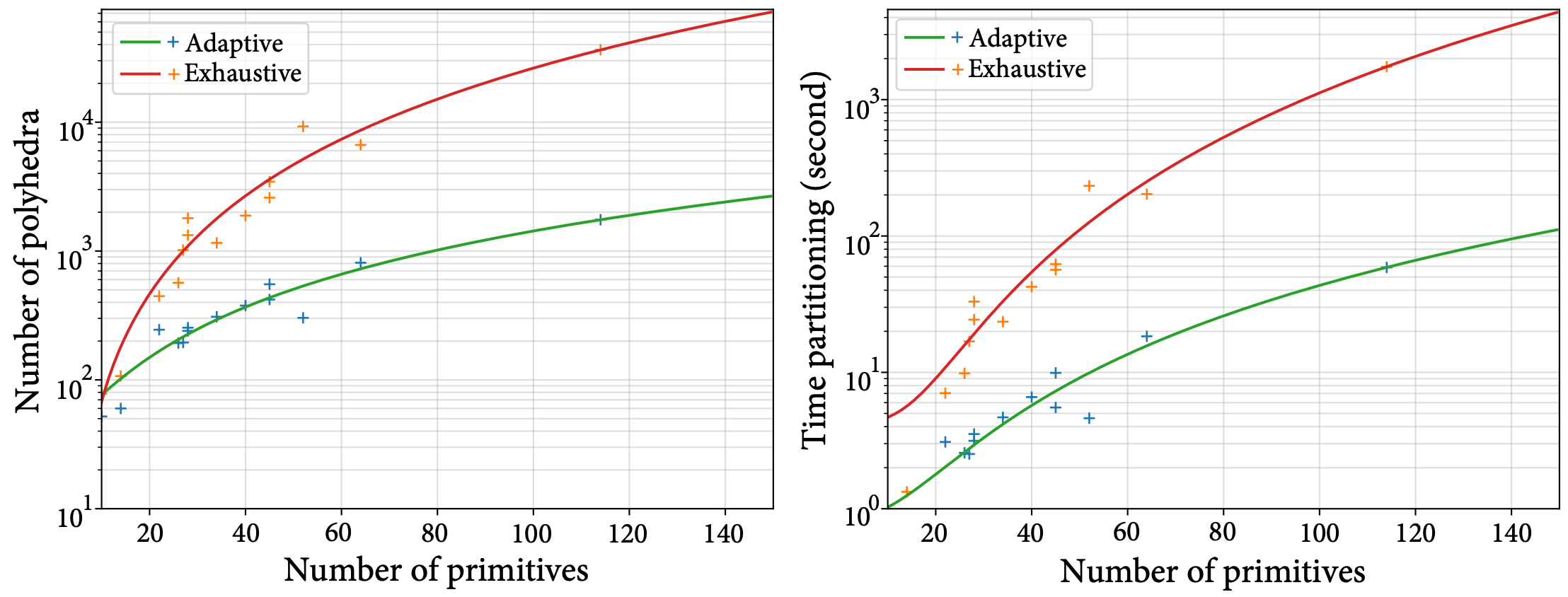
Why adaptive?

Adaptive space partitioning can significantly reduce computations for cell complex creation, compared to the exhaustive counterpart. The excessive number of cells from the latter not only hinders computation but also inclines to defective surfaces on subtle structures where inaccurate labels are more likely to be assigned.

Run the benchmark on the number of candidate cells and runtime among adaptive partitioning, exhaustive partitioning, and SageMath's hyperplane arrangements:

python misc/benchmark.py

How can abspy be used for surface reconstruction?

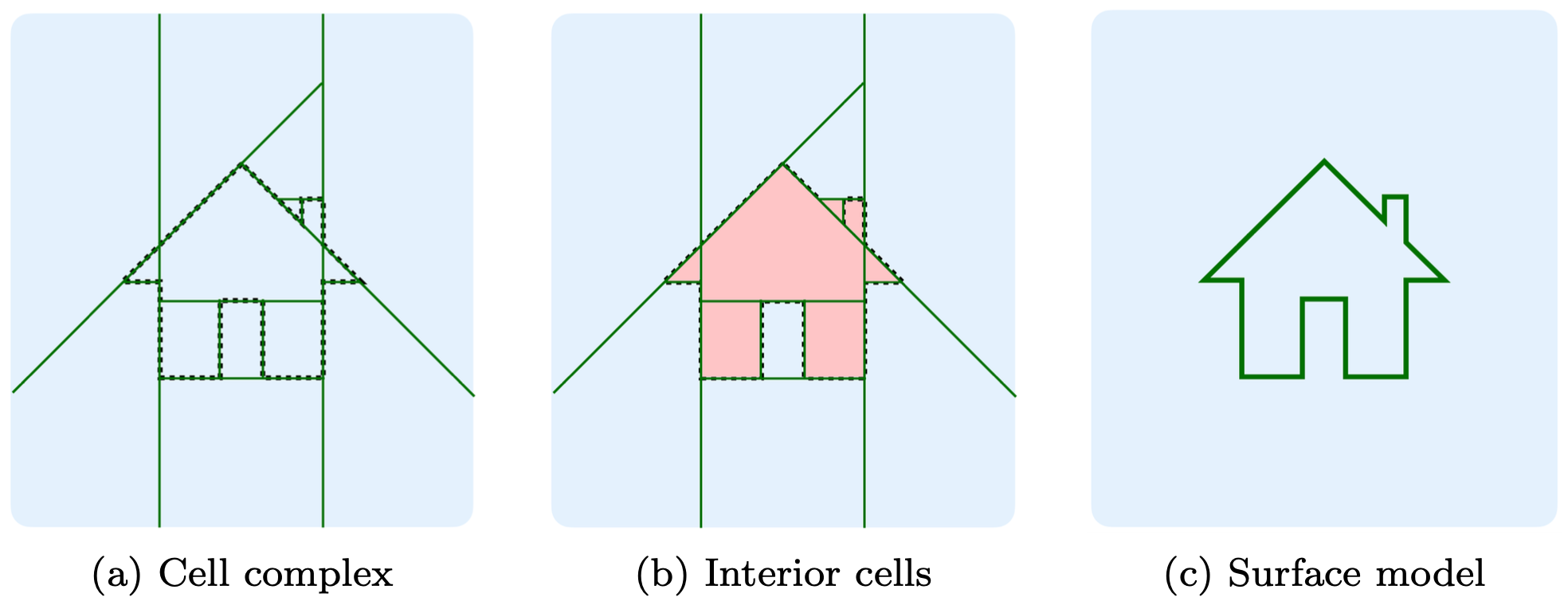
With the cell complex constructed and its adjacency maintained, surface reconstruction can be addressed by a graph cut solver that classifies each cell as being inside or outside the object. The surface exists in between adjacent cells where one is inside and the other is outside — exactly where the cut is performed. For more information, refer to Points2Poly that wraps abspy for building surface reconstruction.

License

MIT

Citation

If you use abspy in a scientific work, please consider citing the paper:

@article{chen2022points2poly,
  title = {Reconstructing compact building models from point clouds using deep implicit fields},
  journal = {ISPRS Journal of Photogrammetry and Remote Sensing},
  volume = {194},
  pages = {58-73},
  year = {2022},
  issn = {0924-2716},
  doi = {https://doi.org/10.1016/j.isprsjprs.2022.09.017},
  url = {https://www.sciencedirect.com/science/article/pii/S0924271622002611},
  author = {Zhaiyu Chen and Hugo Ledoux and Seyran Khademi and Liangliang Nan}
}

yhexie/abspy