SpatialDE is a method to identify genes which significantly depend on spatial coordinates in non-linear and non-parametric ways. The intended applications are spatially resolved RNA-sequencing from e.g. Spatial Transcriptomics, or in situ gene expression measurements from e.g. SeqFISH or MERFISH.
Additionally, SpatialDE provides automatic expression histology, a method that groups genes into common spatial patterns (and conversely reveal histological patterns based on gene coexpression).
This repository contains both the implementations of our methods, as well as case studies in applying it.
The key features of our method are
- Unsupervised - No need to define spatial regions
- Non-parametric and non-linear expression patterns
- Automatic histology based on spatially coexpressed genes
- Extremely fast - Transcriptome wide tests takes only a few minutes on normal computers
The primary implementation is as a Python 3 package, and can be installed from the command line by
$ pip install spatialde
(This should only take a minute or so on a typical system)
To see usage example of SpatialDE either keep reading, or look in the
Analysis directory. The following examples are provided:
BreastCancer- Transcriptome wide study on breast cancer tissue from Spatial Transcriptomics.
Frog- A time course of RNA-seq ("1-d space") of Xenopus development.
MERFISH- Expression from single cells in a region of an osteoblast culture using the MERFISH technology with 140 probes.
MouseOB- Spatial Transcriptomics assay of a slice of Mouse Olfactory Bulb. (Also see below)
SeqFISH- Expression counts of single cells from mouse hippocampus using the SeqFISH technology with 249 probes.
If you wish to look at the data used or run the notebooks and scripts
from start to finish, the data needs to be fetched using git lfs,
a plugin to git for managing large files.
Installation instructions are available on the
projects website. Once git lfs is
installed and you have cloned this repository, data can be downloaded by
running git lfs pull from inside any repository directory.
If you are having problems using git lfs, all the data are available on figshare here: https://figshare.com/articles/software/SpatialDE/17065217
Below follows a typical usage example in interactive form.
%pylab inline
import pandas as pd
rcParams['axes.spines.right'] = False
rcParams['axes.spines.top'] = False
import NaiveDE
import SpatialDEPopulating the interactive namespace from numpy and matplotlib
As an example, let us look at spatially dependent gene expression in Mouse Olfactory Bulb using a data set published in Stahl et al 2016. With the authors method, hundreds of locations on a tissue slice can be sampled at once, and gene expression is measured by sequencing in an unbiased whole-transcriptome manner.
counts = pd.read_csv('Analysis/MouseOB/data/Rep11_MOB_0.csv', index_col=0)
counts = counts.T[counts.sum(0) >= 3].T # Filter practically unobserved genes
print(counts.shape)
counts.iloc[:5, :5](262, 14859)
| Nrf1 | Zbtb5 | Ccnl1 | Lrrfip1 | Bbs1 | |
|---|---|---|---|---|---|
| 16.92x9.015 | 1 | 1 | 1 | 2 | 1 |
| 16.945x11.075 | 0 | 0 | 3 | 2 | 2 |
| 16.97x10.118 | 0 | 1 | 1 | 0 | 0 |
| 16.939x12.132 | 1 | 0 | 1 | 0 | 4 |
| 16.949x13.055 | 0 | 0 | 0 | 3 | 0 |
sample_info = pd.read_csv('Analysis/MouseOB/MOB_sample_info.csv', index_col=0)
counts = counts.loc[sample_info.index] # Align count matrix with metadata table
sample_info.head(5)| x | y | total_counts | |
|---|---|---|---|
| 16.92x9.015 | 16.920 | 9.015 | 18790 |
| 16.945x11.075 | 16.945 | 11.075 | 36990 |
| 16.97x10.118 | 16.970 | 10.118 | 12471 |
| 16.939x12.132 | 16.939 | 12.132 | 22703 |
| 16.949x13.055 | 16.949 | 13.055 | 18641 |
We can plot the x and y coordinates in the sample info table to see which locations of the tissue slice has been sampled.
figsize(6, 4)
plt.scatter(sample_info['x'], sample_info['y'], c='k');
plt.axis('equal');Our method assumes normally distributed noise, but the data we are using is from expression counts, and empirically seems to follow a negative binomial distribution. We use technique by Anscombe to approximately transform the data to normal distributed noise.
Secondly, library size or sequencing depth of the spatial samples will bias the expression of every gene. We use linear regression to account for this effect before performing the spatial test.
norm_expr = NaiveDE.stabilize(counts.T).T
resid_expr = NaiveDE.regress_out(sample_info, norm_expr.T, 'np.log(total_counts)').TFor the sake of this example, let's just run the test on 1000 random genes. This should just take a few seconds. With our very fast implementation, testing all 14,000 genes takes about 10 minutes.
sample_resid_expr = resid_expr.sample(n=1000, axis=1, random_state=1)
X = sample_info[['x', 'y']]
results = SpatialDE.run(X, sample_resid_expr)INFO:root:Performing DE test INFO:root:Pre-calculating USU^T = K's ... INFO:root:Done: 0.11s INFO:root:Fitting gene models INFO:root:Model 1 of 10 INFO:root:Model 2 of 10 INFO:root:Model 3 of 10 INFO:root:Model 4 of 10 INFO:root:Model 5 of 10 INFO:root:Model 6 of 10 INFO:root:Model 7 of 10 INFO:root:Model 8 of 10 INFO:root:Model 9 of 10 INFO:root:Model 10 of 10
The result will be a DataFrame with P-values and other relevant
values for each gene.
The most important columns are
g- The name of the genepval- The P-value for spatial differential expressionqval- Significance after correcting for multiple testingl- A parameter indicating the distance scale a gene changes expression over
results.head().T| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| FSV | 0.999955 | 2.0597e-09 | 2.0597e-09 | 2.0597e-09 | 2.0597e-09 |
| M | 4 | 4 | 4 | 4 | 4 |
| g | 2410016O06Rik | Arpp19 | Srsf7 | Wbp7 | Cpsf3l |
| l | 0.402001 | 0.402001 | 0.402001 | 0.402001 | 0.402001 |
| max_delta | 4.53999e-05 | 4.85165e+08 | 4.85165e+08 | 4.85165e+08 | 4.85165e+08 |
| max_ll | -52.2589 | -107.685 | -114.477 | -112.664 | -49.1672 |
| max_mu_hat | -0.826851 | -2.21845 | -6.67811 | -2.25044 | 0.146089 |
| max_s2_t_hat | 0.666985 | 1.04203e-08 | 9.22126e-08 | 1.07257e-08 | 2.20142e-10 |
| model | SE | SE | SE | SE | SE |
| n | 260 | 260 | 260 | 260 | 260 |
| s2_FSV | 1.94342 | 0.253788 | 47.2945 | 0.363388 | 4.48293 |
| s2_logdelta | 6.81931e+08 | 4.3315e+16 | 8.07194e+18 | 6.20209e+16 | 7.65119e+17 |
| time | 0.00134182 | 0.00104499 | 0.000994921 | 0.000999928 | 0.00106692 |
| BIC | 126.761 | 237.613 | 251.196 | 247.571 | 120.577 |
| max_ll_null | -53.706 | -107.686 | -114.478 | -112.665 | -49.1681 |
| LLR | 1.44715 | 0.000964007 | 0.000964011 | 0.000964007 | 0.00096401 |
| pval | 0.228986 | 0.975231 | 0.975231 | 0.975231 | 0.975231 |
| qval | 0.975231 | 0.975231 | 0.975231 | 0.975231 | 0.975231 |
results.sort_values('qval').head(10)[['g', 'l', 'qval']]| g | l | qval | |
|---|---|---|---|
| 890 | Kcnh3 | 1.907609 | 0.001512 |
| 772 | Pcp4 | 1.135190 | 0.013843 |
| 736 | Igfbp2 | 1.135190 | 0.013843 |
| 800 | Gng13 | 1.907609 | 0.022632 |
| 646 | Naaa | 0.675535 | 0.051705 |
| 749 | Map1b | 1.135190 | 0.051705 |
| 826 | Gng4 | 1.907609 | 0.051705 |
| 724 | Fmo1 | 1.135190 | 0.096710 |
| 714 | Slc38a3 | 1.135190 | 0.096710 |
| 712 | Hpcal4 | 1.135190 | 0.107360 |
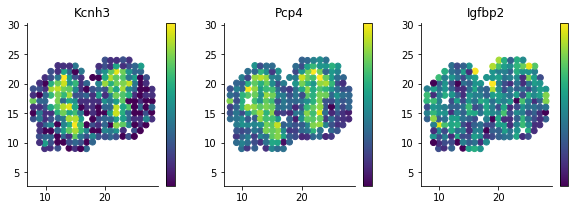
We detected a few spatially differentially expressed genes, Cck and Ptn for example.
A simple way to visualize these genes is by plotting the x and y coordinates as above, but letting the color correspond to expression level.
figsize(10, 3)
for i, g in enumerate(['Kcnh3', 'Pcp4', 'Igfbp2']):
plt.subplot(1, 3, i + 1)
plt.scatter(sample_info['x'], sample_info['y'], c=norm_expr[g]);
plt.title(g)
plt.axis('equal')
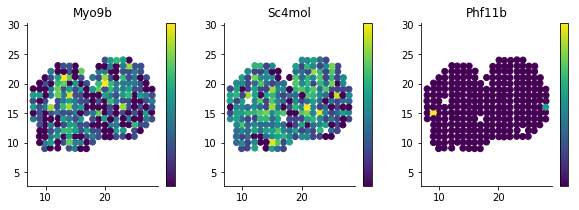
plt.colorbar(ticks=[]);For reference, we can compare these to genes which are not spatially DE
results.sort_values('qval').tail(10)[['g', 'l', 'qval']]| g | l | qval | |
|---|---|---|---|
| 334 | Tmem70 | 0.402001 | 0.975231 |
| 335 | Rnf20 | 0.402001 | 0.975231 |
| 336 | Zfp85-rs1 | 0.402001 | 0.975231 |
| 337 | C1qtnf7 | 0.402001 | 0.975231 |
| 338 | Ap4b1 | 0.402001 | 0.975231 |
| 339 | Psma4 | 0.402001 | 0.975231 |
| 340 | Aldh3b1 | 0.402001 | 0.975231 |
| 341 | Hdx | 0.402001 | 0.975231 |
| 328 | Zfp113 | 0.402001 | 0.975231 |
| 999 | Preb | 9.052138 | 0.975231 |
figsize(10, 3)
for i, g in enumerate(['Myo9b', 'Sc4mol', 'Phf11b']):
plt.subplot(1, 3, i + 1)
plt.scatter(sample_info['x'], sample_info['y'], c=norm_expr[g]);
plt.title(g)
plt.axis('equal')
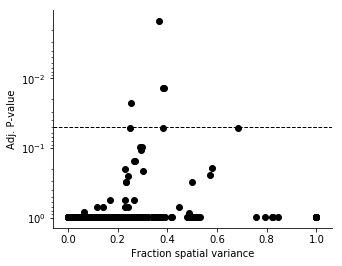
plt.colorbar(ticks=[]);In regular differential expression analysis, we usually investigate the relation between significance and effect size by so called volcano plots. We don't have the concept of fold change in our case, but we can investigate the fraction of variance explained by spatial variation.
figsize(5, 4)
plt.yscale('log')
plt.scatter(results['FSV'], results['qval'], c='black')
plt.axhline(0.05, c='black', lw=1, ls='--');
plt.gca().invert_yaxis();
plt.xlabel('Fraction spatial variance')
plt.ylabel('Adj. P-value');To perform automatic expression histology (AEH), the genes should be
filtered by SpatialDE significance. For this example, let us use a very
weak threshold. But in typical use, filter by qval < 0.05
sign_results = results.query('qval < 0.05')AEH requires two parameters: the number of patterns, and the characteristic lengthscale for histological patterns.
For some guidance in picking the lengthscale l we can look at the
optimal lengthscale for the signficant genes.
sign_results['l'].value_counts()1.135190 11 1.907609 4 0.675535 4 3.205604 1 Name: l, dtype: int64
Here we see that the lengthscale on average is ~1.5, to use some extra
spatial covariance, we put this paramater to l = 1.8.
For the number of patterns, we try C = 3.
histology_results, patterns = SpatialDE.aeh.spatial_patterns(X, resid_expr, sign_results, C=3, l=1.8, verbosity=1)iter 0, ELBO: -9.48e+08 iter 1, ELBO: -4.20e+08, delta_ELBO: 5.28e+08 iter 2, ELBO: -4.20e+08, delta_ELBO: 7.63e+02 iter 3, ELBO: -4.20e+08, delta_ELBO: 2.07e+02 iter 4, ELBO: -4.20e+08, delta_ELBO: 8.03e+01 iter 5, ELBO: -4.20e+08, delta_ELBO: 3.40e+00 iter 6, ELBO: -4.20e+08, delta_ELBO: 6.62e-02 iter 7, ELBO: -4.20e+08, delta_ELBO: 2.75e-03 iter 8, ELBO: -4.20e+08, delta_ELBO: 3.96e-03 iter 9, ELBO: -4.20e+08, delta_ELBO: 7.49e-05 Converged on iter 9
After fitting the AEH model, the function returns two DataFrames,
one with pattern membership information for each gene:
histology_results.head()| g | membership | pattern | |
|---|---|---|---|
| 564 | AI593442 | 1.0 | 1 |
| 619 | Arhgef9 | 1.0 | 1 |
| 632 | 6330403K07Rik | 1.0 | 1 |
| 646 | Naaa | 1.0 | 0 |
| 712 | Hpcal4 | 1.0 | 2 |
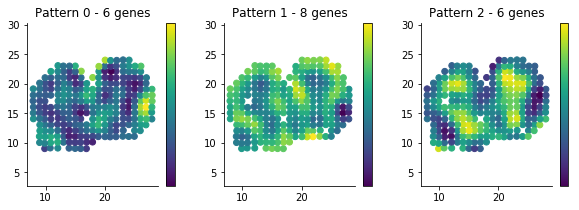
And one with realizations for the underlying expression for each histological pattern.
We can visualize this underlying expression in the tissue context as we would for any individual gene.
figsize(10, 3)
for i in range(3):
plt.subplot(1, 3, i + 1)
plt.scatter(sample_info['x'], sample_info['y'], c=patterns[i]);
plt.axis('equal')
plt.title('Pattern {} - {} genes'.format(i, histology_results.query('pattern == @i').shape[0] ))
plt.colorbar(ticks=[]);It is usually interesting to see what the coexpressed genes determining a histological pattern are:
for i in histology_results.sort_values('pattern').pattern.unique():
print('Pattern {}'.format(i))
print(', '.join(histology_results.query('pattern == @i').sort_values('membership')['g'].tolist()))
print()Pattern 0 Naaa, Aebp1, Mfap3l, Fmo1, 2810002D19Rik, Gng13 Pattern 1 Map2, Arhgef9, AI593442, 6330403K07Rik, Slc38a3, Igfbp2, Nmb, Map1b Pattern 2 Hpcal4, Snap25, Pcp4, Gng4, Ppfia2, Kcnh3