CICV2022仿真赛题1-大学生方程式赛车

View video Demo · Report Bug · Request Feature

About CICV2022 仿真赛

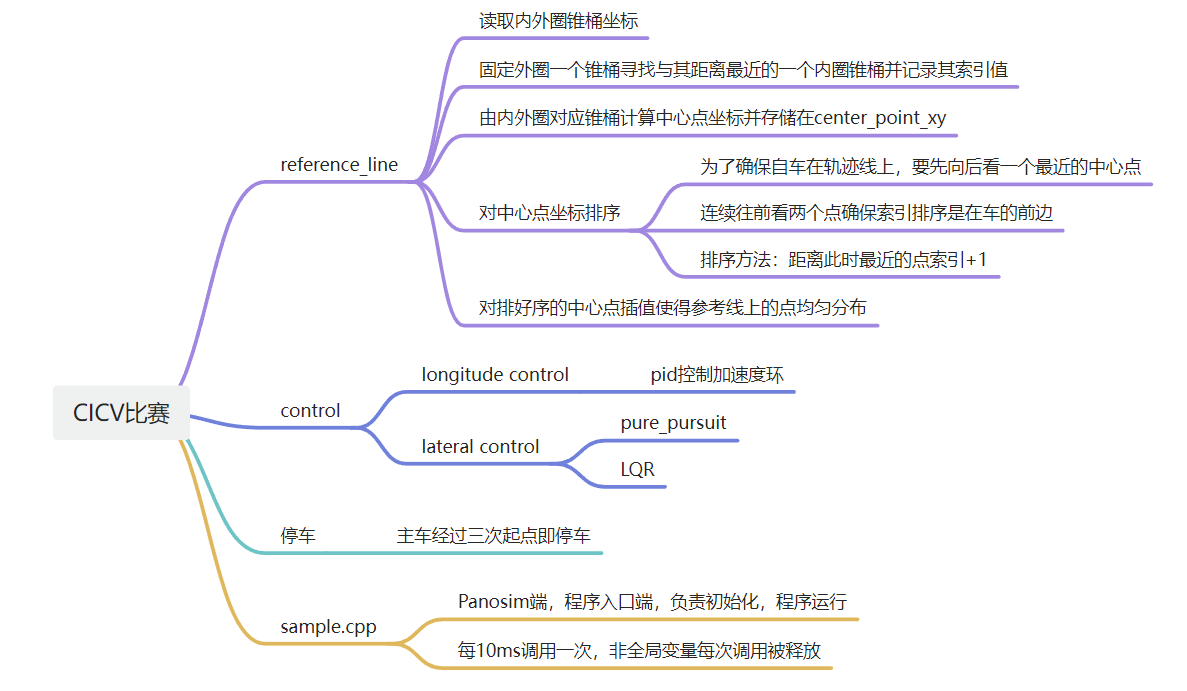
本项目为CICV2022仿真赛题1-大学生方程式赛车。
项目需要识别两侧红蓝桩桶，生成参考线，控制车辆竞速完成比赛。决赛地图包含多个发卡弯，U型弯，大直道，需要良好的横纵向结合能力方能完成比赛。
在这里很感谢CICV比赛承办方和Panosim平台，感谢团队成员的共同努力，最终我们取得全国第一的成绩。
仿真平台为Panosim，程序编译使用vs2019。
决赛视频

Getting Started

Prerequisites

Simply perform the following steps：

eigen

安装Eigen3

代码框架

生成的路径

图中黄色为局部路径，整个项目都是基于车身坐标系建立的。

编译运行

在vs2019上进行编译，编译生成的dll文件位于相对文件夹\Sample\SampleSchedulerNode\bin\x64\Release\SampleScheduler_142.dll。
生成的dll文件拷贝到Panosim工作目录D:\PanoSimDatabase\Plugin\Agent中即可。

Result

通过比赛调试，掌握了纯跟踪和LQR横向控制方法，对PID调参有了更深的认识。

LQR理解

目标函数为： $J=e_{rr}^{T}Qe_{rr}+u^{T}Ru$，目标函数此二次型在约束 $\dot e_{rr}=Ae_{rr}+Bu$ 下存在最小值。

将代价函数化简为：

$$ J=[e_d,\dot e_d,e_{\varphi},\dot e_{\varphi}] \begin{bmatrix} Q_{11}&0&0&0\\ 0&Q_{22}&0&0\\ 0&0&Q_{33}&0\\ 0&0&0&Q_{44} \end{bmatrix} \begin{bmatrix} e_{d}\\ \dot e_{d}\\ e_{\varphi}\\ \dot e_{\varphi} \end{bmatrix}+ u[R]u^{T} $$

Q11：对应横向误差分析，值越大横向误差越小，反之相反。
Q22：值变化不大，一般取较小值，比如1。
Q33：对应航向误差分析，值越大航向误差越小，反之相反。
Q44：值变化不大，一般取较小值，比如1。
R：越大控制越小，不容易过急弯；越小控制越大，容易过急弯，控制不稳定。

纯跟踪设计

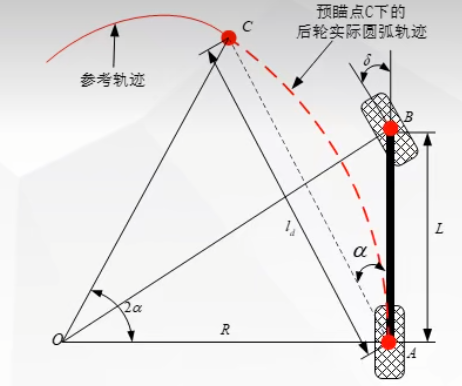
车辆在行驶过程中需要预瞄道路上的一点来计算转角。
推导过程：
在三角形OAC中应用正弦定理：
$\frac{l_d}{\sin(2\alpha)}=\frac{R}{\sin\frac{(\pi-2\alpha)}{2}}$，化简为： $\sin(\alpha)=\frac{l_d}{2R}$ (1)
$\tan\delta=\frac{L}{R}$，化简为： $\delta =\arctan\frac{L}{R}$ (2)
联立（1）、（2）得：
$\delta=\arctan\frac{2Lsin\alpha}{l_d}$，其中 $\alpha$ 为 $\alpha=\arctan\frac{y_c-y_A}{x_c-c_A}$
其中Ld为预瞄距离，R为转弯半径， $\delta=\alpha$ 。
纯跟踪近似为比例控制器，推导如下：
横向误差 $e_y=l_d*sin\alpha=\frac{l_d^2}{2L}tan\delta=\frac{l_d^2}{2L}\delta$
所以纯跟踪本质上是一个比例控制器，跟踪效果由 $\frac{l_d^{2}}{2L}$ 决定，通常定义ld为关于速度的一次多项式。

PID调参

时域表达 $u(t)=u_P(t)+u_I(t)+u_D(t)=K_Pe(t)+K_I\int e(t)dt+K_D\frac{de(t)}{dt}$
双环PID是对位置和速度误差进行设计。
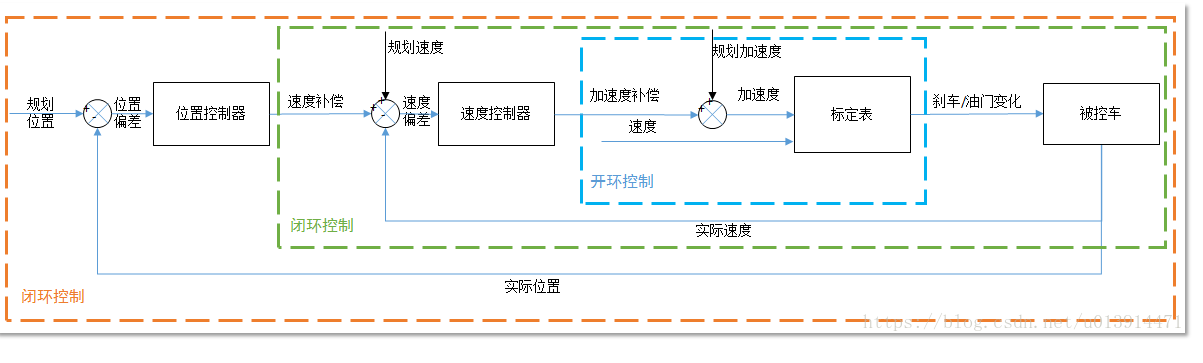
调参注意事项：
Kp：一般情况下不用太大就可以得到较好的收敛速度和精度。
Ki：一般比Kp要小，减小静差。 Kd：避免超调。

Acknowledgments

比赛能够完成还要感谢我的队友们，他们都很给力！

Liuzy0908/cell