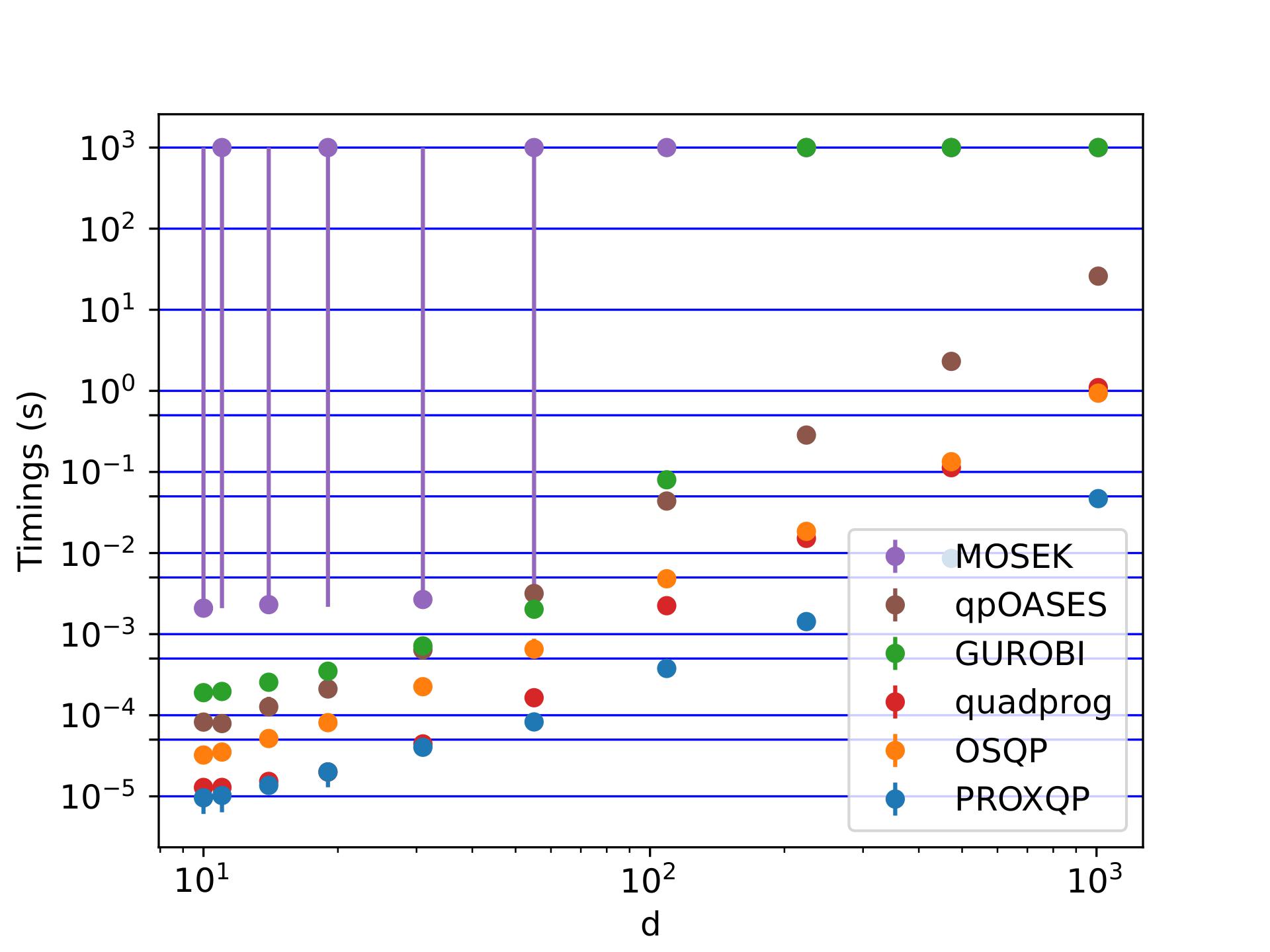
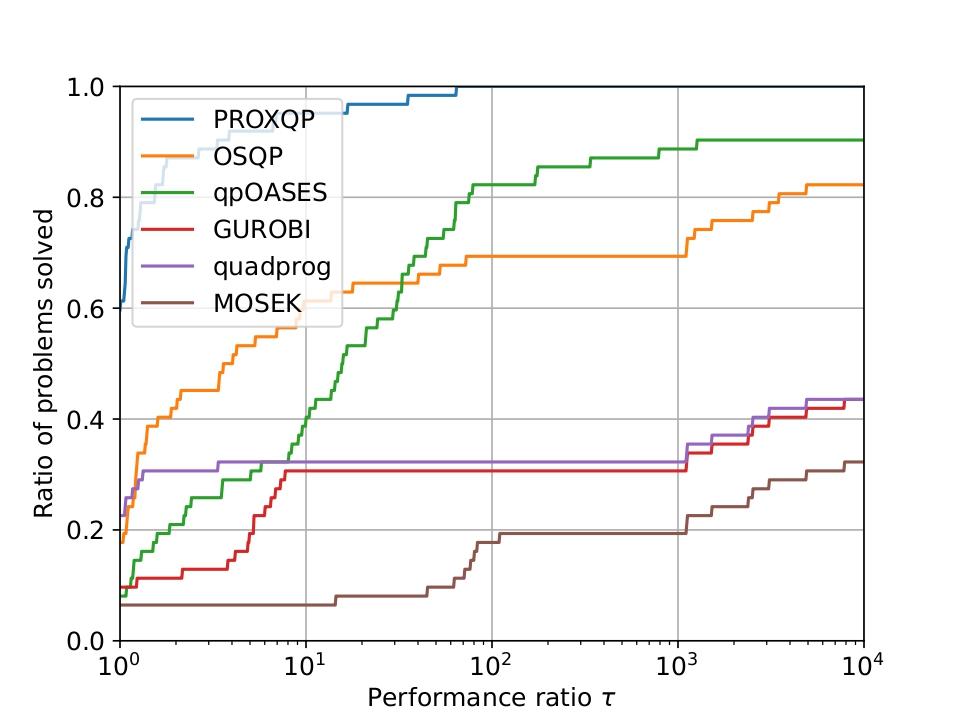
These are the scripts to compare the following Quadratic Program (QP) solvers
- PROXQP (with dense backend)
- OSQP
- GUROBI
- MOSEK
- qpOASES
- quadprog
The whole API comes from the one developped by the authors of OSQP. We thank them a lot for their rigorous approach.
The detailed description of these tests is available in this paper.
To run these scripts you need standard python libraries: pandas, matplotlib, numpy, scipy, scikit-learn, and cvxpy, which can be installed using for example conda:
conda install pandas matplotlib numpy scipy cvxpy scikit-learnYou need further as well to install the solvers gurobi, mosek, OSQP, quadprog and qpOASES. The first four can be installed for example using conda:
conda install -c gurobi gurobi
conda install -c mosek mosek
conda install -c conda-forge osqp
conda install -c omnia quadprogGurobi and Mosek require a license for working. Note that if you are an academic, they provide specific and temporary free licenses.
Finally, for installing qpOASES, you should look at their install file in their github repository.
All the scripts come with options (default to False)
--parallelfor parallel execution across instances--verbosefor verbose solvers output (they can be slower than necessary while printing)--high_accuracyfor high accuracyeps=1e-09solver settings + optimality checks
Note that the parallel option has not be tested for the paper benchmarks.
The problems are all randomly generated as described in the ProxQP paper. Problem instances include
- Inequality and Equality Constrained QP,
- Pure Inequality Degenerate QP,
- Pure Inequality QP without strictly convex Hessian matrix.
We generate the problems using the scripts in the problem_classes folder.
To execute these tests run
python run_benchmark_problems.pyFor Convex Quadratic Programs with inequality and equality constraints, when asking for a high accuracy (e.g., 1.E-9), the resulting shifted geometric means are, for dense problems
| PROXQP | quadprog | OSQP | GUROBI | MOSEK | qpOASES |
|---|---|---|---|---|---|
| 1.0 | 20.4 | 18.2 | 5177.8 | 38131.0 | 282.6 |
and for sparser one (i.e., a ratio of sparsity of around 15%)
| PROXQP | quadprog | OSQP | GUROBI | MOSEK | qpOASES |
|---|---|---|---|---|---|
| 1.0 | 19.3 | 3.5 | 6938.0 | 76844.2 | 260.6 |
These results have been obtained with a 11th Gen Intel(R) Core(TM) i7-11850H @ 2.50GHz CPU.
These are the hard problems from the Maros Meszaros testset converted using CUTEst and the scripts in the maros_meszaros_data/ folder.
To execute these tests run
python run_maros_meszaros_problems.pyThe resulting shifted geometric means are when asking for a high accuracy (e.g., 1.E-9)
| PROXQP | quadprog | OSQP | GUROBI | MOSEK | qpOASES |
|---|---|---|---|---|---|
| 1.0 | 105.8 | 14.2 | 114.2 | 194.9 | 4.5 |
At lower accuracy (e.g., 1.E-3), the resulting shifted geometric means are
| PROXQP | quadprog | OSQP | GUROBI | MOSEK | qpOASES |
|---|---|---|---|---|---|
| 1.0 | 1543.3 | 108.5 | 637.3 | 175.3 | 17.1 |
These results have been obtained as well with a 11th Gen Intel(R) Core(TM) i7-11850H @ 2.50GHz CPU.
If you are using these benchmarks for your work, please cite the ProxQP paper:
@inproceedings{bambade:hal-03683733,
TITLE = {{PROX-QP: Yet another Quadratic Programming Solver for Robotics and beyond}},
AUTHOR = {Antoine Bambade, Sarah El-Kazdadi, Adrien Taylor, Justin Carpentier},
URL = {https://hal.inria.fr/hal-03683733},
BOOKTITLE = {{RSS 2022 - Robotics: Science and Systems}},
ADDRESS = {New York, United States},
YEAR = {2022},
MONTH = June,
PDF = {https://hal.inria.fr/hal-03683733/file/Yet_another_QP_solver_for_robotics_and_beyond.pdf},
HAL_ID = {hal-03683733},
HAL_VERSION = {v1},
}