abhileshborode/Unscented-Kalman-Filter

In this project we utilize an Unscented Kalman Filter to estimate the state position_x,position_y, velocity, yaw,yaw_rate of a moving object of interest with noisy lidar and radar measurements.

Unscented Kalman Filter

In this project we utilize an Unscented Kalman Filter to estimate the state position_x,position_y, velocity, yaw,yaw_rate of a moving object of interest with noisy lidar and radar measurements.

This project involves the Term 2 Simulator which can be downloaded here.

This repository includes two files that can be used to set up and intall uWebSocketIO for either Linux or Mac systems. For windows you can use either Docker, VMware, or even Windows 10 Bash on Ubuntu to install uWebSocketIO. Please see the uWebSocketIO Starter Guide page in the classroom within the EKF Project lesson for the required version and installation scripts.

Once the install for uWebSocketIO is complete, the main program can be built and ran by doing the following from the project top directory.

1. mkdir build
2. cd build
3. cmake ..
4. make
5. ./UnscentedKF

INPUT: values provided by the simulator to the c++ program

["sensor_measurement"] => the measurment that the simulator observed (either lidar or radar)

OUTPUT: values provided by the c++ program to the simulator

["estimate_x"] <= kalman filter estimated position x ["estimate_y"] <= kalman filter estimated position y ["rmse_x"] ["rmse_y"] ["rmse_vx"] ["rmse_vy"]

---

Other Important Dependencies

• cmake >= 3.5
  • All OSes: click here for installation instructions
• make >= 4.1 (Linux, Mac), 3.81 (Windows)
  • Linux: make is installed by default on most Linux distros
  • Mac: install Xcode command line tools to get make
  • Windows: Click here for installation instructions
• gcc/g++ >= 5.4
  • Linux: gcc / g++ is installed by default on most Linux distros
  • Mac: same deal as make - install Xcode command line tools
  • Windows: recommend using MinGW

Basic Build Instructions

1. Clone this repo.
2. Make a build directory: mkdir build && cd build
3. Compile: cmake .. && make
4. Run it: ./UnscentedKF

Simulation

The image below is a screenshot from the simulator using the Unscented Kalman Filter from this project.

Discussion

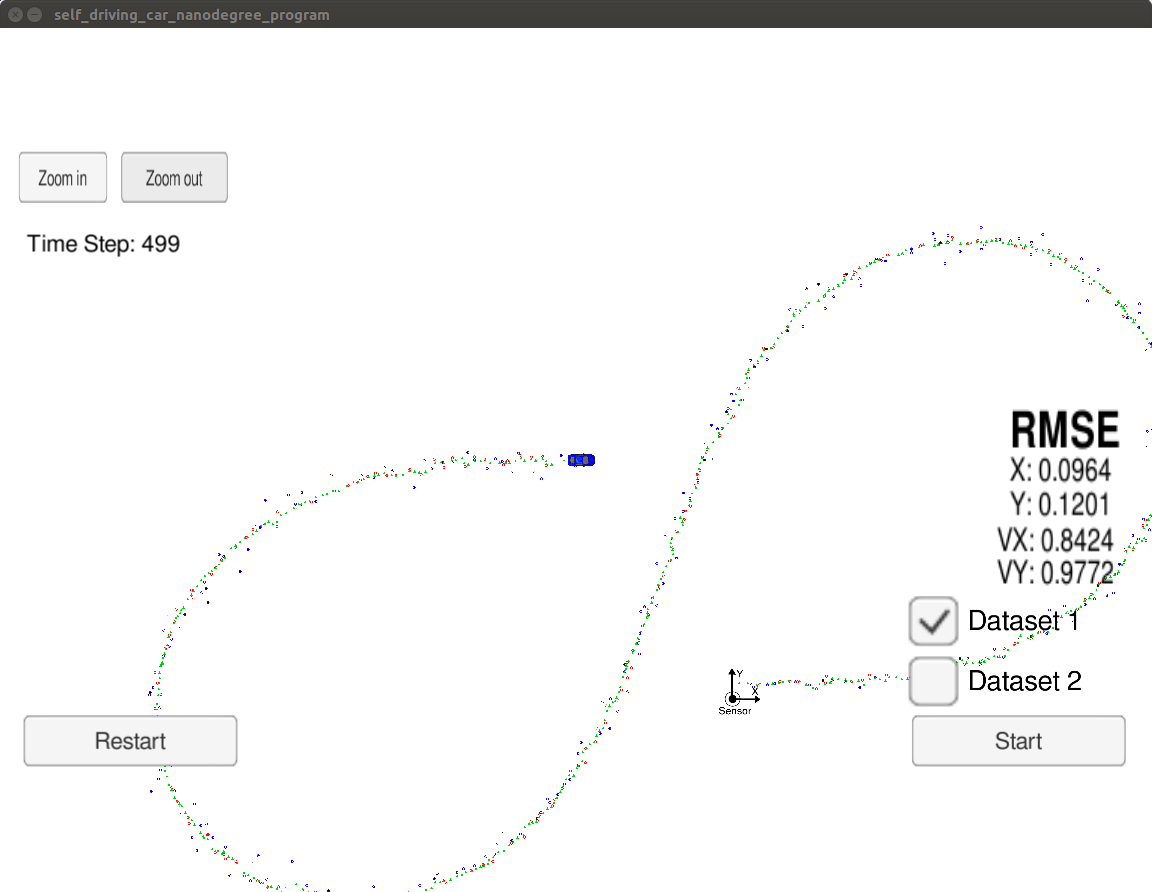
The Unscented Kalman Filter (UKF) estimates a state of an object when dealing with non linear process and measurement models which cannot be linearised like in case of the Extended Kalman Filter. This is mainly due to the CTRV motion model used in the Unscented Kalman Filter, which is better able to model acceleration (change in direction). The CTRV motion model contains non-linear equations which the UKF can accomodate. The EKF used the a jacobian to create linear equations and we used only 1 mean point in case of EKF unlike UKF where we use multiple sigma points to model the distribution .