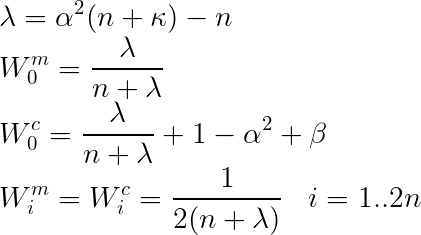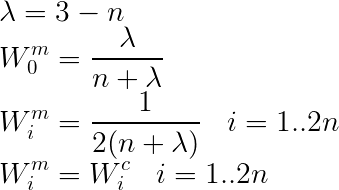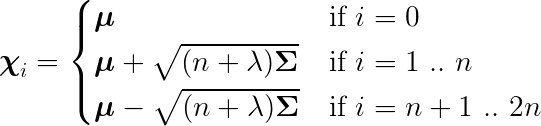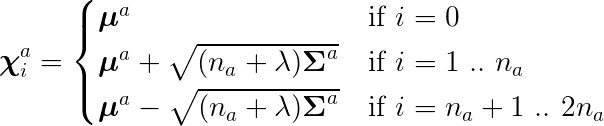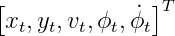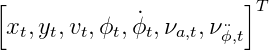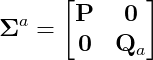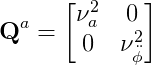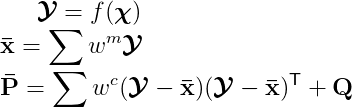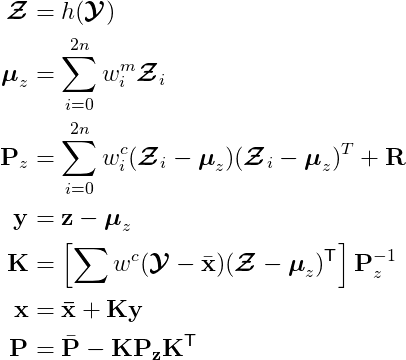Unscented Kalman filtering in Python and C++ for tracking and localization
This repo implements an unscented Kalman filter (UKF) class in python, to be further integrated into tracking and localization related projects. I take inspiration from and am informed by the repos such as:
- https://github.com/rlabbe/filterpy
- https://github.com/AtsushiSakai/PythonRobotics/tree/master/Localization.
The requirements for the UKF class are:
- The UKF class should be self-contained -- i.e. it should include all the function blocks within a single class, including the Sigma point generation and update.
- The UKF class should have the flexibility of taking any forms of process and measurement functions as input.
- The UKF class should be able to deal with both additive and non-additive process noise. In particular, the UKF class should have the capability of implementing Sigma points augmentation as often required for non-additive process noise. This capability, to the best of my knowledge, is not adequately addressed in the two repos mentioned above.
ukf.py-- implements the UKF classprocess_measurement.py-- implements a few process and measurement modeld. This script will be regularly updated.ukf_ctrv_test.ipynb-- an Ipython notebook that illustrates the tracking of highway vehicle using UKF and constant turn rate and velocity (CTRV) model.
The possible confusions and difficulties in implementing UKF could happen in Sigma points augmentation. The augmentation is often needed when the process noise is non-additive. To avoid possible confusions, I summarize in the following table the dimension of Sigma points and augmented Sigma points used in state, process, and measurement, respectively. Note that n and n_\a represent the dimension of the (regular) state and augmented state, respectively.
| Sigma Points | Augmented Sigma points | |
|---|---|---|
| State | (2n + 1, n ) | (2n_a + 1, n_a) |
| Process | (2n + 1, n ) | (2n_a + 1, n ) |
| Measurement | (2n + 1, n_z) | (2n_a + 1, n_z) |
The calculation of the weights is implemented as in the following function:
def calculate_weights(self):
"""
Calculate the weights associated with sigma points. The weights depend on parameters dim_x, alpha, beta,
and gamma. The number of sigma points required is 2 * dim_x + 1
"""
# dimension for determining the number of sigma points generated
dim = self.dim_x if not self.augmentation else self.dim_xa
if self.sigma_mode == 1:
lambda_ = self.alpha_**2 * (dim + self.kappa_) - dim
Wc = np.full(2*dim + 1, 1. / (2*(dim + lambda_))) #
Wm = np.full(2*dim + 1, 1. / (2*(dim + lambda_)))
Wc[0] = lambda_ / (dim + lambda_) + (1. - self.alpha_**2 + self.beta_)
Wm[0] = lambda_ / (dim + lambda_)
elif self.sigma_mode == 2:
lambda_ = 3 - dim
Wc = np.full(2*dim + 1, 1./ (2*(dim + lambda_)))
Wm = np.full(2*dim + 1, 1./ (2*(dim + lambda_)))
Wc[0], Wm[0] = lambda_ /(dim + lambda_), lambda_ /(dim + lambda_)
return (Wc, Wm)
Here we consider two approaches (modes). In Mode 1, /lambda not only depends on the dimension of the state (or augmented state), but also on parameters such as /alpha and /kappa. Weights for mean and covariance matrix are calculated (slight) differently.
In Mode 2, /lambda depends only on the dimension. In addition, the weights for mean and covariance are the same.
The Sigma points are calculated as the following:
The augmented Sigma points are calculated as the following:
The update_sigma_pts calculated the Sigma points or augmented Sigma points
def update_sigma_pts(self):
"""
Create (update) Sigma points during the prediction stage
"""
if not self.augmentation:
dim, x, P = self.dim_x, self.x, self.P
else:
dim = self.dim_xa
x = np.concatenate([self.x, self.xa])
P = block_diag(self.P, self.Qa)
if self.sigma_mode == 1:
lambda_ = self.alpha_**2 * (dim + self.kappa_) - dim
elif self.sigma_mode == 2:
lambda_ = 3 - dim
U = cholesky((dim + lambda_) * P)
self.sigma_pts[0] = x
for k in range (dim):
self.sigma_pts[k + 1] = x + U[k]
self.sigma_pts[dim + k + 1] = x - U[k]
Consider an example of CTRV model, if the impact of the noise is not considered, the process model is as following:
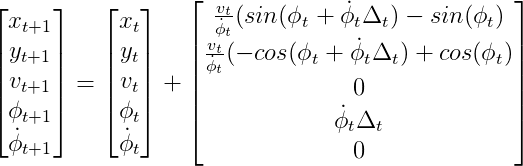
If we also consider the impact of non-additive noise, the process model is as following:
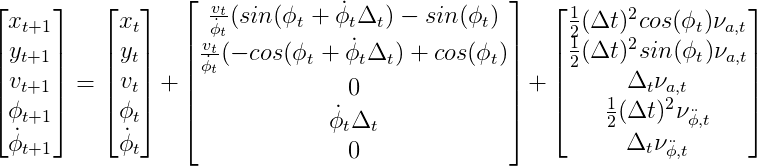 .
.
In this case, the dimension of the state need to augmented. That is, from a regular state of dimension of five, to an augmented state of dimension seven.
Note that to calculate the augmented Sigma points, we need to use \Sigma_a as follows,
The process noise matrix Q_a is given by
This line implements the above operations:
P = block_diag(self.P, self.Qa)
The formula of the prediction stage is given by:
Note that for non-additive noise, the process noise covariance matrix Q, by default, is set to zero.
The computation of process Sigma points is implemented in compute_process_sigma_pts ():
def compute_process_sigma_pts(self, input_sigma_pts, **fx_args):
"""
Calculate the sigam points transformed the process function fx
Input:
input_sigma_pts: input sigma points
**fx_args: keywords/arguments associated with process/system function defined as fx
Output:
output_sigma_pts: sigma points transformed by the process
"""
fx, dt = self.fx, self.dt
n_sigmas, _ = input_sigma_pts.shape
output_sigma_pts = zeros([n_sigmas, self.dim_x])
for i, s in enumerate(input_sigma_pts):
output_sigma_pts[i] = fx(s, dt, **fx_args)
return output_sigma_pts
The prediction stage is implemented in prediction (), which calls calculate_mean_covariance (0
def prediction(self, **fx_args):
"""
Prediction, calculated the prior state estimate and covariance
Input:
**fx_args: keywords/arguments associated with process/system function defined as fx
"""
fx = self.fx
self.update_sigma_pts( ) # update the sigma points
sigma_pts = self.sigma_pts
process_sigma_pts = self.compute_process_sigma_pts(sigma_pts, **fx_args) # sigma points transformed by the process
self.sigma_pts_f = process_sigma_pts
# mean and covariance of sigma transformed mean and covariance
if not self.x_resid:
self.x, self.P = self.calculate_mean_covariance(process_sigma_pts, self.Q)
else:
self.x, self.P = self.calculate_mean_covariance(process_sigma_pts, self.Q, adjust = True, indices = self.x_resid_indices)
self.x_prior, self.P_prior = np.copy(self.x), np.copy(self.P)
The update stage is implemented in update(), which calls compute_measurement_sigma_pts().
def update(self, z, **hx_args):
"""
Update step, calculate the (new) posterior state and covariance
Input:
z: measuremnt
**hx_args: keywords/arguments associated with measurement function defined in hx
"""
hx = self.hx
sigmas_f = self.sigma_pts_f
n_sigmas = sigmas_f.shape[0]
# Transform sigma points from state space to measurement space
sigmas_h = self.compute_measurement_sigma_pts(sigmas_f, **hx_args)
self.sigma_pts_h = sigmas_h
if not self.z_resid:
zp, Pz = self.calculate_mean_covariance(sigmas_h, self.R)
else:
zp, Pz = self.calculate_mean_covariance(sigmas_h, self.R, adjust = True,
indices = self.z_resid_indices)
self.S = Pz
# Compute cross variance of the state and the measurement
Pxz = np.zeros((self.dim_x, self.dim_z))
for i in range(n_sigmas):
x_r = sigmas_f[i] - self.x
if self.x_resid:
x_r = self.residual(x_r, self.x_resid_indices)
z_r = sigmas_h[i] - zp
if self.z_resid:
z_r = self.residual(z_r, self.z_resid_indices)
Pxz += self.Wc[i] * outer(x_r, z_r)
self.SI = inv(Pz)
K = dot(Pxz, inv(Pz)) # Kalman gain
self.K = K
# New state estimae and covariance maxtrix
self.y = z - zp
self.x = self.x + dot(K, z - zp)
self.P = self.P - dot(K, Pz).dot(K.T)
self.x_post = self.x.copy()
self.P_post = self.P.copy()
self.z = deepcopy(z)