michaelnaps/four

For my personal study of simple real/complex Fourier methods and their application to various systems.

Fourier Series and Animations

UNDER DEVELOPMENT

This small Python library was inspired by the 3Brown1Blue video linked here. After watching this video I took some time to remind myself of the structure of a Fourier series (which I, at one point, taught in ungrad.) before building the classes in the package FOUR.

The idea of a 2-D Fourier series is relatively simple. The general theory states that any function, $f$, which maps between two domains such that $f : \mathbb{X} \rightarrow \mathbb{Y}$ can be represented by an infinite sum of $\cos(x)$ and $\sin(x)$ terms.

$$ f(x) = \sum_{k=0}^\infty \left[ A_k \sin(\frac{\pi k x}{L}) + B_k \cos(\frac{\pi k x}{L}) \right] $$

Where $x \in \mathbb{X}$ and $f(x) \in \mathbb{Y}$.

References:
    A. Gilat and V. Subramaniam, Numerical methods for engineers and
        scientists: an introduction with applications using matlab, 3. ed.
        Hoboken, NJ: Wiley, 2014.

---

Imprinting Temporal-dynamics onto a Grid

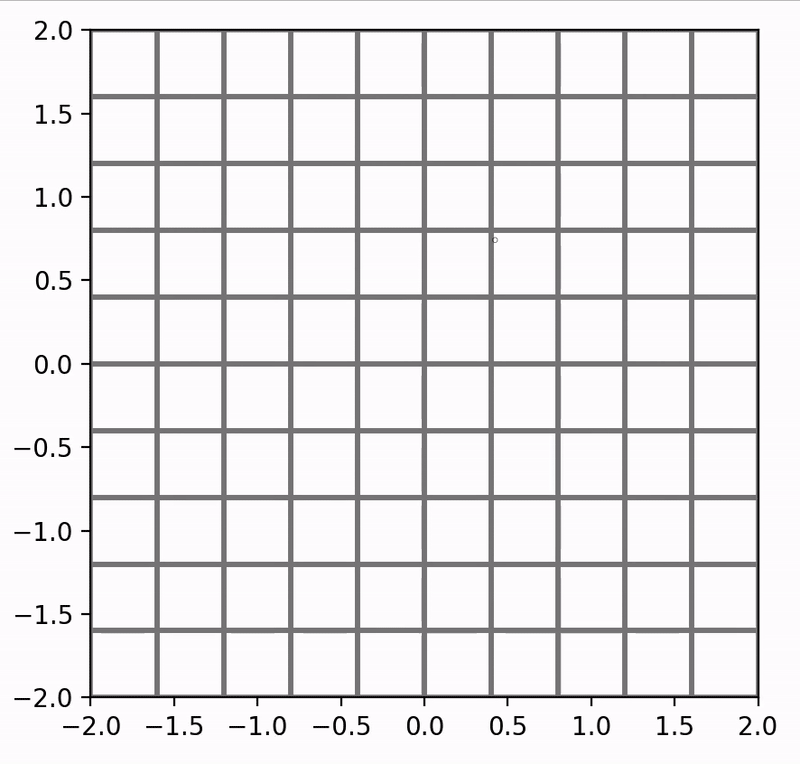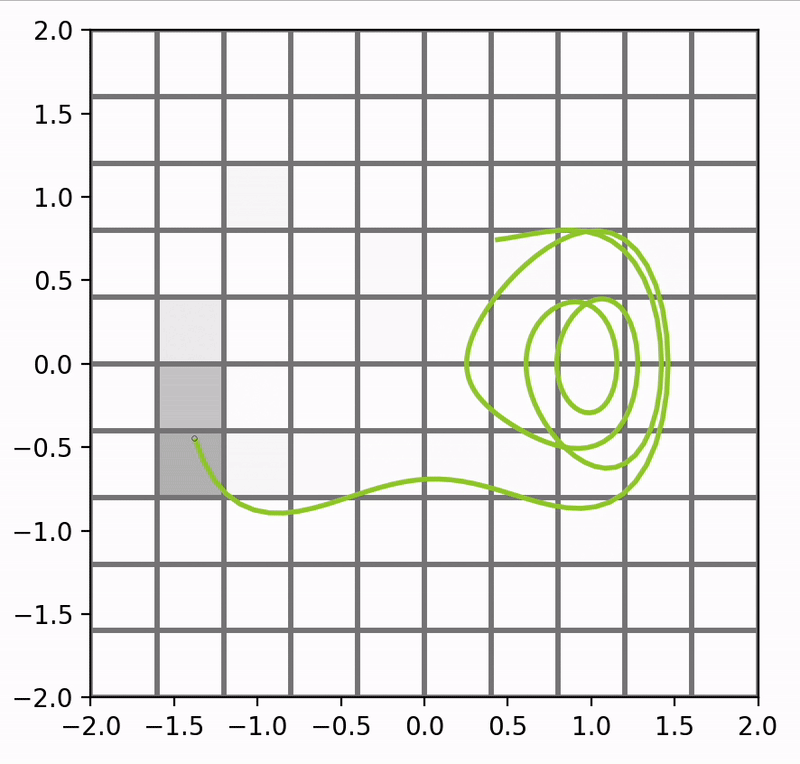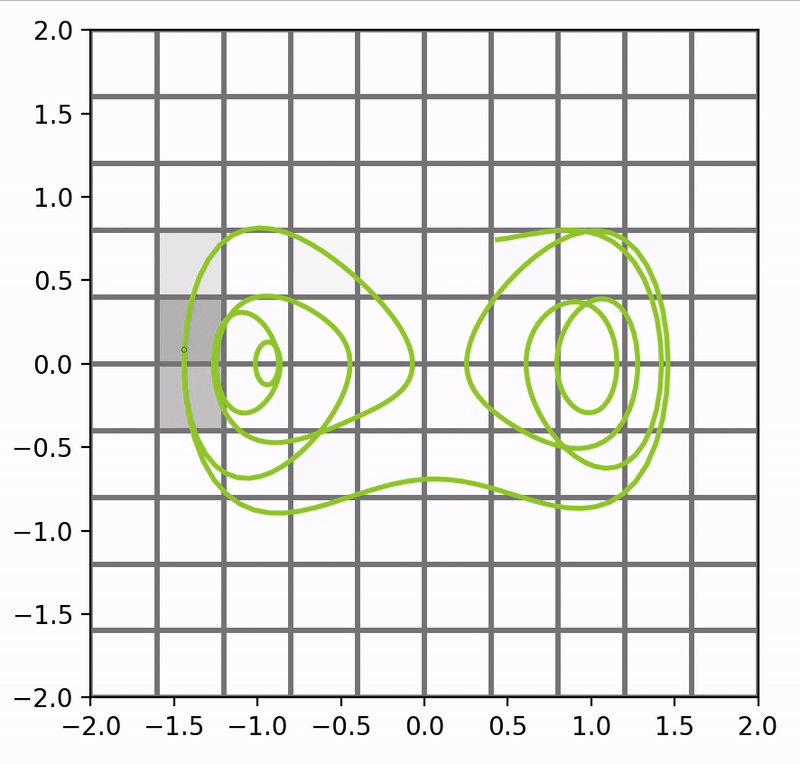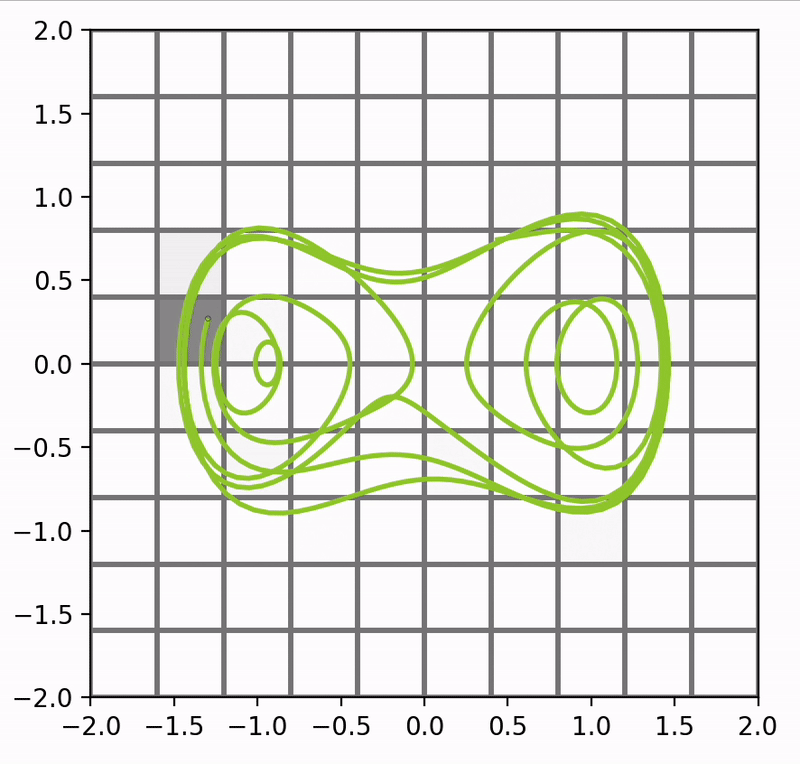
In this quick example I have imprinted the motion of the duffing oscillator (as begun from a single set point) onto a grid. Each space can be made visible or invisible dependent on whether the point is present in that cell. That is,

$$ c_{i,j} = \begin{cases} 1 & \text{if $x(t)$ is present} \\ 0 & \text{otherwise} \end{cases} $$

Where $c_{i,j}$ is the binary value for the $j$-th cell in the $i$-th row. The binary grid was saved at each step of the simulation and used to calculate the Fourier transform. This resulted in a playback that looks like...