ReHLine is designed to be a computationally efficient and practically useful software package for large-scale empirical risk minimization (ERM) problems.
- Documentation: https://rehline-python.readthedocs.io
- Project homepage: https://rehline.github.io
- GitHub repo: https://github.com/softmin/ReHLine-python
- PyPi: https://pypi.org/project/rehline
- Paper: NeurIPS | 2023
The ReHLine solver has four appealing "linear properties":
- It applies to any convex piecewise linear-quadratic loss function, including the hinge loss, the check loss, the Huber loss, etc.
- In addition, it supports linear equality and inequality constraints on the parameter vector.
- The optimization algorithm has a provable linear convergence rate.
- The per-iteration computational complexity is linear in the sample size.
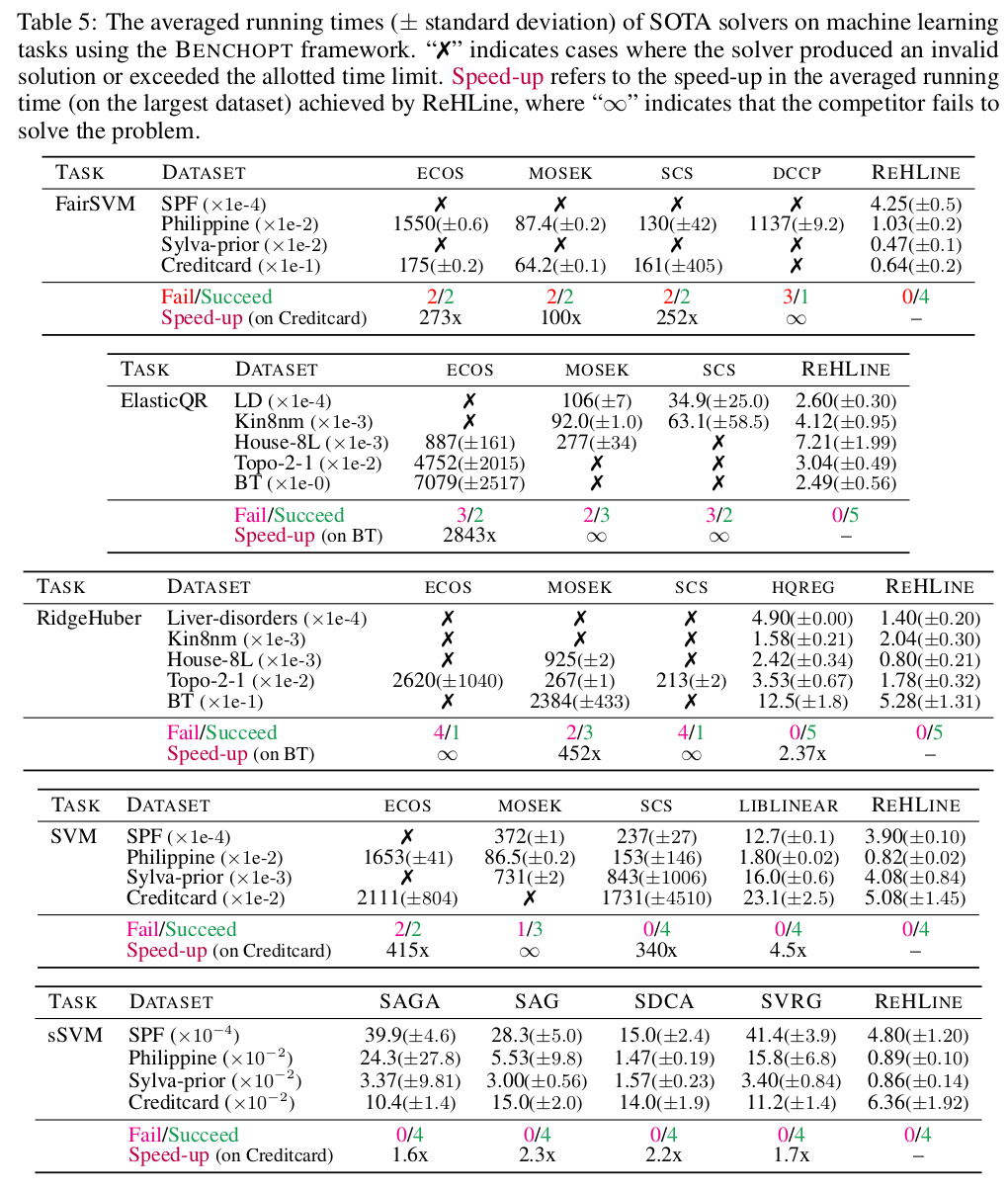
Some existing problems of recent interest in statistics and machine learning can be solved by ReHLine, and we provide reproducible benchmark code and results at the ReHLine-benchmark repository.
| Problem | Results |
|---|---|
| FairSVM | Result |
| ElasticQR | Result |
| RidgeHuber | Result |
| SVM | Result |
| Smoothed SVM | Result |