PyMarchingCubes is a fork from PyMCubes, with a different implementation of the actual marching function (see 'marching_cubes/src/marchingcubes.h').
It fixes some issues of the original implementation that let to wrong triangulation (visible in triangles that are larger than the actual 'marching cell').
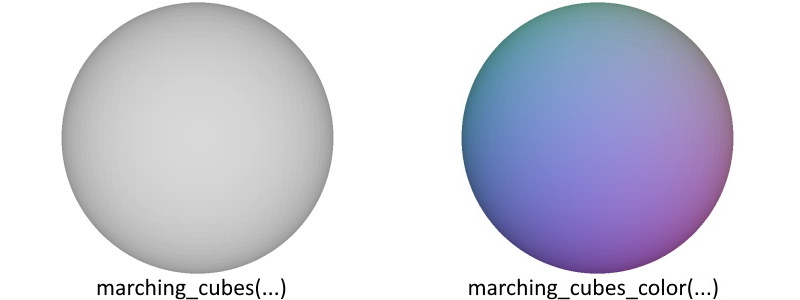
The module also includes a marching cubes with color interpolation:
marching_cubes_color and marching_cubes_color_func.
Have a look at the 'examples/spheres.py' file.
Basically, it is called with marching_cubes_color(sdf_volume, rgb_volume, iso_level) assuming a 3D grid for the sdf values (dim_x,dim_y,dim_z) and a 4D grid for the colors (dim_x,dim_y,dim_z,3).
The export functions for obj and off files are adapted accordingly to handle the vertex colors.
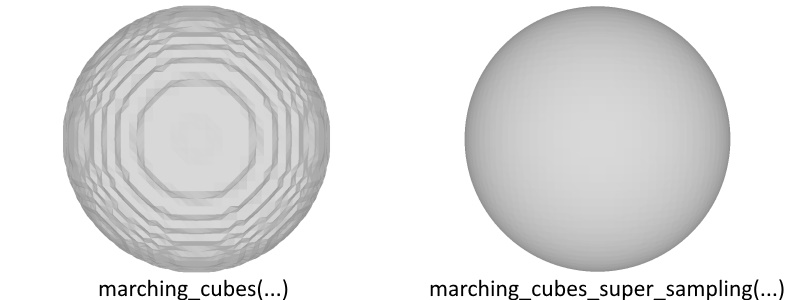
In case you are using a truncated signed distance function, you might miss the correct zero-crossing because of undersampling. Increasing the sample volume grows cubically, instead one can also subsample along the edges of a coarser volume to find a better approximation of the zero-crossing.
This subsampling of the edges is achieved by sampling along the x,y,z axis independently with higher resolution (e.g., you sample (dim_x + (dim_x-1)*edge_sampling, dim_y, dim_z) for the edges along the x axis).
The computational cost grow linear with the number of subsamples (e.g. 10 subsamples result in ~30 times more samples that you have to provide (since you need 10 times more samples per axis)).
A modified marching cubes implementation can be called via marching_cubes_super_sampling(sdf_x, sdf_y, sdf_z, iso_level).
Have a look at the sphere example.
Other than that, this repository is the same as the original (https://github.com/pmneila/PyMCubes).
git clone https://github.com/JustusThies/PyMarchingCubes.git
cd PyMarchingCubes
git clone https://gitlab.com/libeigen/eigen.git
python setup.py install
The following example creates a NumPy volume with spherical iso-surfaces and
extracts one of them (i.e., a sphere) with mcubes.marching_cubes. The result
is exported to sphere.dae:
>>> import numpy as np
>>> import marching_cubes as mcubes
# Create a data volume (30 x 30 x 30)
>>> X, Y, Z = np.mgrid[:30, :30, :30]
>>> u = (X-15)**2 + (Y-15)**2 + (Z-15)**2 - 8**2
# Extract the 0-isosurface
>>> vertices, triangles = mcubes.marching_cubes(u, 0)
# Export the result to sphere.dae
>>> mcubes.export_mesh(vertices, triangles, "sphere.dae", "MySphere")Alternatively, you can use a Python function to represent the volume instead of
a NumPy array:
>>> import numpy as np
>>> import marching_cubes as mcubes
# Create the volume
>>> f = lambda x, y, z: x**2 + y**2 + z**2
# Extract the 16-isosurface
>>> vertices, triangles = mcubes.marching_cubes_func((-10,-10,-10), (10,10,10),
... 100, 100, 100, f, 16)
# Export the result to sphere.dae (requires PyCollada)
>>> mcubes.export_mesh(vertices, triangles, "sphere.dae", "MySphere")
# Or export to an OBJ file
>>> mcubes.export_obj(vertices, triangles, 'sphere.obj')Note that using a function to represent the volumetric data is much slower
than using a NumPy array.
Many segmentation methods build binary masks to separate inside and outside areas of the segmented object. When passing these binary mask to the marching cubes algorithm the resulting mesh looks jagged. The following code shows an example with a binary array embedding a sphere.
x, y, z = np.mgrid[:100, :100, :100]
binary_sphere = (x - 50)**2 + (y - 50)**2 + (z - 50)**2 - 25**2 < 0
# Extract the 0.5-levelset since the array is binary
vertices, triangles = mcubes.marching_cubes(binary_sphere, 0.5)PyMCubes provides the function mcubes.smooth that takes a 2D or 3D binary
embedding function and produces a smooth version of it.
smoothed_sphere = mcubes.smooth(binary_sphere)
# Extract the 0-levelset (the 0-levelset of the output of mcubes.smooth is the
# smoothed version of the 0.5-levelset of the binary array).
vertices, triangles = mcubes.marching_cubes(smoothed_sphere, 0)mcubes.smooth builds a smooth embedding array with negative values in the
areas where the binary embedding array is 0, and positive values in the areas
where it is 1. In this way, mcubes.smooth keeps all the information from the
original embedding function, including fine details and thin structures that
are commonly eroded by other standard smoothing methods.