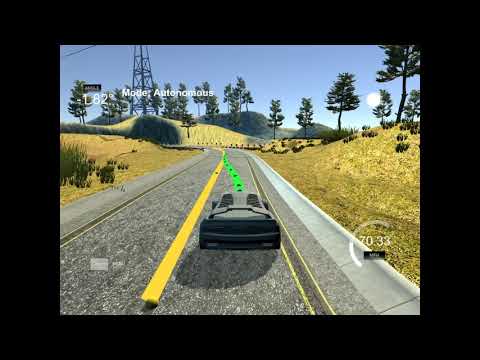
In the is project I try to navigate through the lake track yet another time, but this time I'll be using MPC to guide the vehicle. MPC deals with the problem of following a trajectory by optimizing the actuator values to achieve the optimal trajectory, this is different from other controllers such as the PID. MPC will control the steering angel delta δ as well as the acceleration which is controlled by the throttle.
MPC works on optimizing the error for each N steps of dt duration. I used a simple kinematic bicycle model which accounts for the vehicle heading, but its not a complicated model that accounts for tire friction and others variables. Here is the formula of the model:
It uses the vehicle position x and y, the heading Ψ, velocity v, Cross Track Error cte, and the heading Error eΨ, this model is implemented on line line 133 of the MPC.cpp
N and dt or the duration of trajectory So I started where the lecture suggested with N to 25 and dt to 0.05 I kept decreasing the N value because a high N value gives smoother result, but its computationally expensive so I wanted the lowest value that could give the optimal result which was 12; However, I left the dt value at 0.05 which produced really good results and is convenient for latency calculation later.
Here I mainly transform all points to vehicle coordinate space using the toCarCoordinates() method at line line 71 of the main.cpp because all of our work will be from the vehicle's perspective. First I translate the values around the origin and align the x axis to the heading of the car.
I fit the newly obtained vehicle space waypoints to a 3rd order polynomial using polyfit() method at line line 50 of the main.cpp, here I used 3 order polynomial rather than the 1st order that was used in the lectures to have a better curvier fit rather than a linear one because its not a linear model .
The project adds a **100 milliseconds ** delay for setting the actuator values, this counts as 2 steps for the chosen dt 2 * 0.005 = 0.1 seconds. Now we need to account for the delay cause if we use the model as it is we'll always be a 100 ms (2 time steps) late which could have catastrophic consequences in the real world and crash in the simulator at high speeds. So I kept track of previous actuator values for the duration of the latency which in turn includes it in the optimization and negates the effect of the latency. I had to increase most of the indices by 2 to account for the latency.
I added the following variables to the MPC.h
double prev_a{0};
double prev_delta{0.1};
const int latency_timestep = 2;
and used them to constraint the actuator values to the previous values to account for latency as you can see at lines * 204 to 216* of the MPC.cpp.
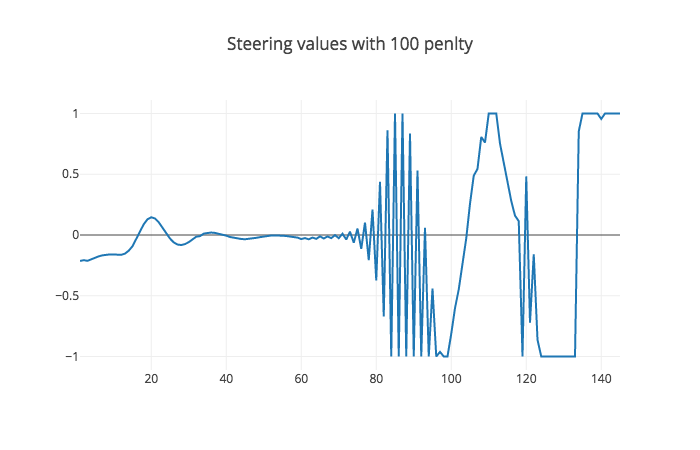
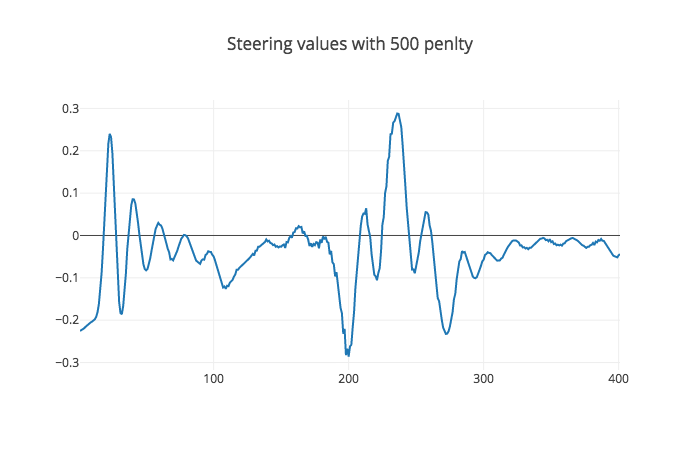
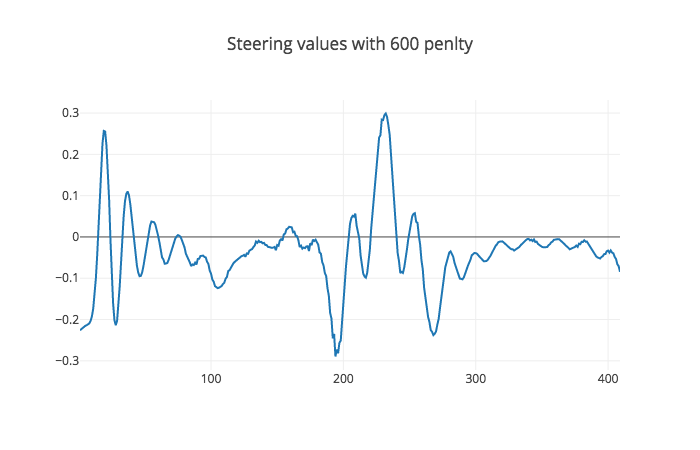
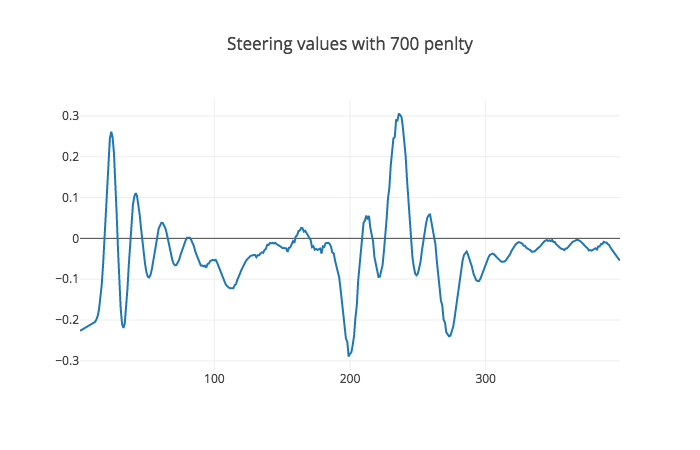
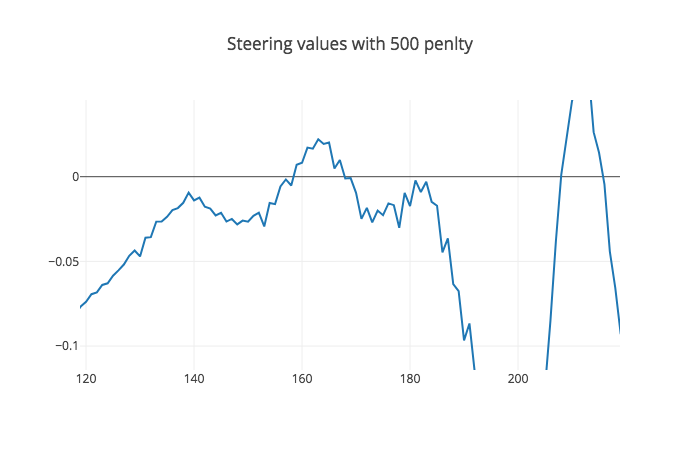
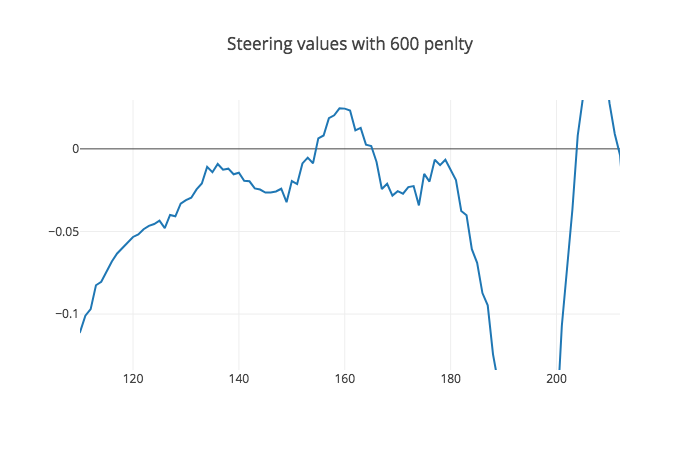
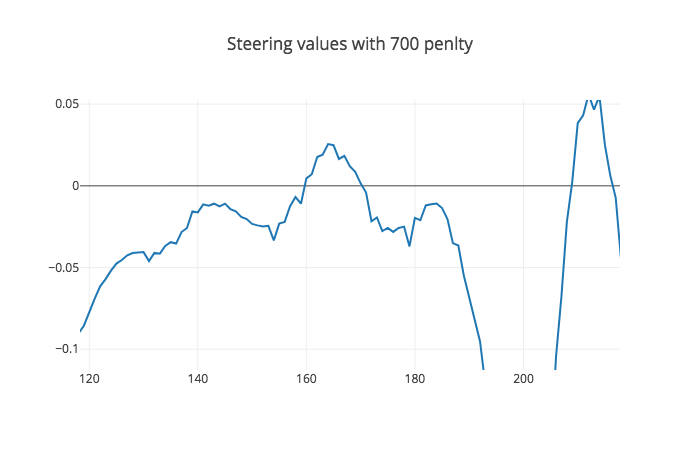
Here I added a penalty as the Tuning MPC part of the MPC lesson suggested. I used multiple values [100, 500, 600, 700] and observed their steering values as you can see in the figures below.
Here the car crashed after 146 steps, so I knew I had to do better.
Here its a far cry from the previous value and the car drives really well around the track without crashing. However, in the lesson it was said that by increasing the value we can get a smoother result so I kept going.
And here is the result for the value of 600 smoother than 500, but not by much so lets go higher.
This one is a bit better than 600 and 2 bits better than 500 and the car drives even smoother, so I'm going to stop here and hope fully test higher numbers later.
They all look alike dont they, well all except for 100 which crashed; however, if we look closer we can see that by increasing the value we get a smoother transtion as you can see here:
500| 600|700|
---|:--:|:--:
So that's why I stuck with 700 as a correction or smoothening value. I noticed that every time we increase the value the peak values go a little higher, so as increasing the value is good for smoothening it elongates the peaks in order to get a smoother turn which could be a problem with higher values.